北师大版八年级数学下册 1.4角平分线 同步检测题 (附答案)
文档属性
| 名称 | 北师大版八年级数学下册 1.4角平分线 同步检测题 (附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 52.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 00:00:00 | ||
图片预览

文档简介
1.4角平分线
同步检测题
一.
选择题
1.
如图所示,OP平分∠AOB,PC⊥OA于C,PD⊥OB于D,则PC与PD的大小关系是(??
)
A.
PC>PD???????????
B.
PC=PD?????????????
C.
PC<PD????????
D.
不能确定
2.
在Rt△ABC中,∠C=90°,AD是角平分线,若BC=10,BD∶CD=3∶2,则点D到AB的距离是(??
)
A.
4???????????????
B.
6???????????
C.
8????????????????D.
10
3.
在△ABC中,∠C=90°,E是AB边的中点,BD是角平分线,且DE⊥AB,则(??
)
A.
BC>AE???????????
B.
BC=AE????????????
C.
BC<AE?????????
D.
以上都有可能
4.
如图所示,点P是∠BAC的平分线AD上一点,PE⊥AC于点E,已知PE=3,则点P到AB的距离是(??
)
A.
3?????????????????????
B.
4?????????????
C.
5?????????????????????
D.
6
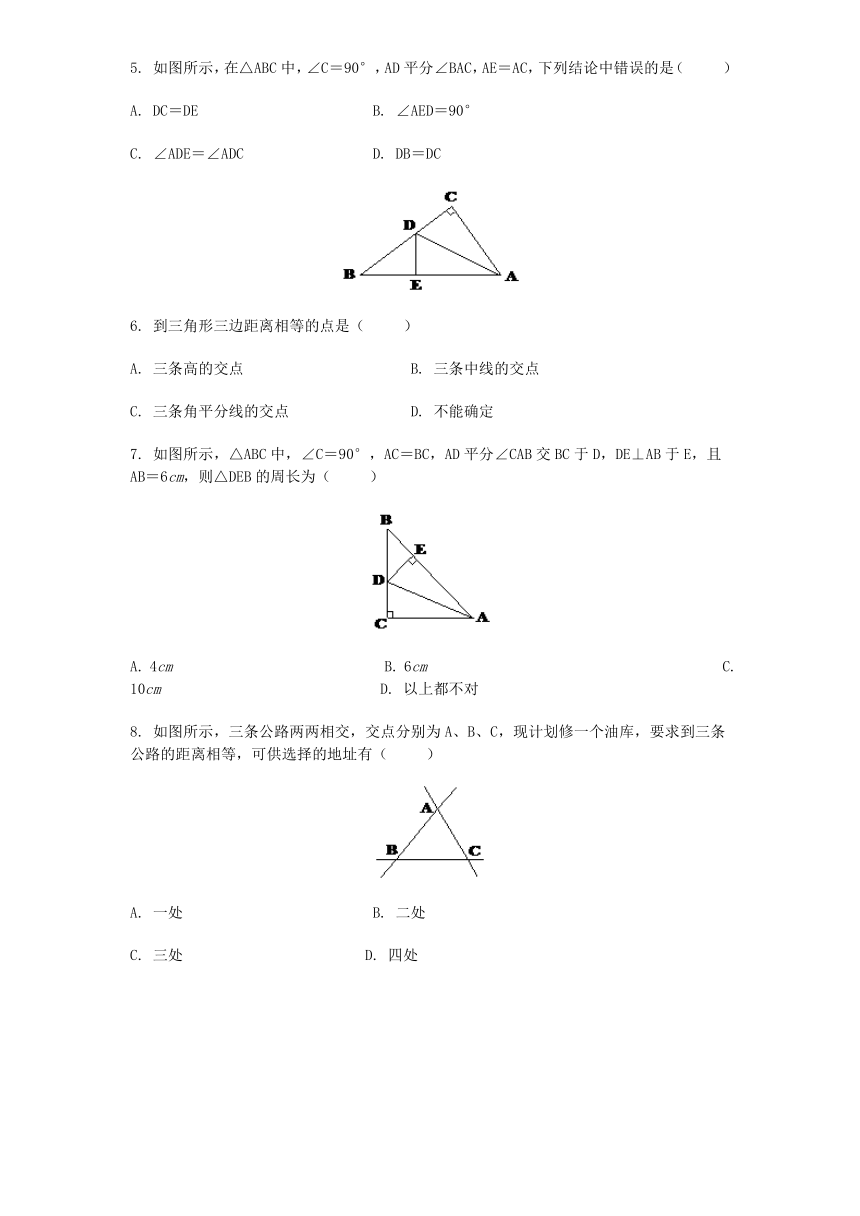
5.
如图所示,在△ABC中,∠C=90°,AD平分∠BAC,AE=AC,下列结论中错误的是(??
)
A.
DC=DE???????????
B.
∠AED=90°???
C.
∠ADE=∠ADC??
D.
DB=DC
6.
到三角形三边距离相等的点是(??
)
A.
三条高的交点???????????B.
三条中线的交点
C.
三条角平分线的交点????????D.
不能确定
7.
如图所示,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6cm,则△DEB的周长为(??
)
A.
4cm??????????????B.
6cm???????????????????
C.
10cm??????????????
D.
以上都不对
8.
如图所示,三条公路两两相交,交点分别为A、B、C,现计划修一个油库,要求到三条公路的距离相等,可供选择的地址有(??
)
A.
一处????????????
B.
二处?????????????????
C.
三处????????????D.
四处
二.
填空题
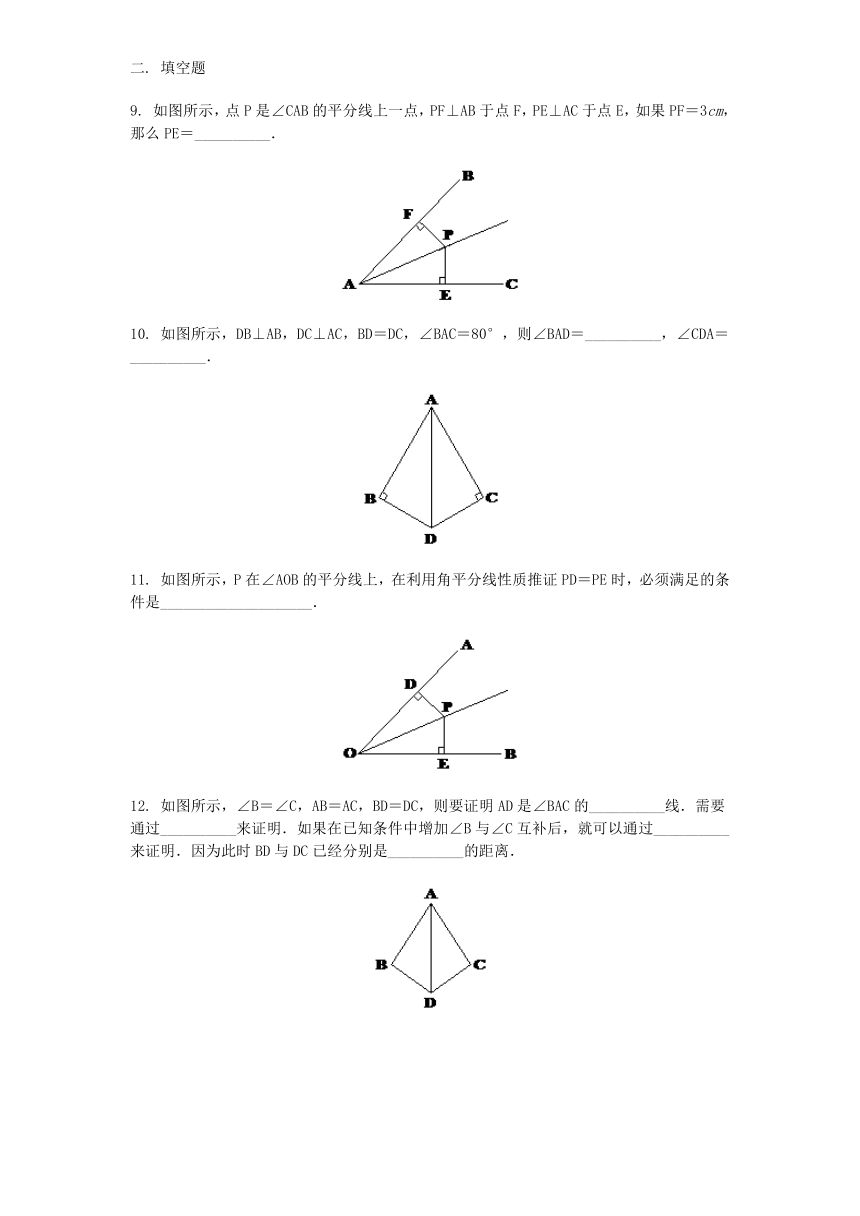
9.
如图所示,点P是∠CAB的平分线上一点,PF⊥AB于点F,PE⊥AC于点E,如果PF=3cm,那么PE=__________.
10.
如图所示,DB⊥AB,DC⊥AC,BD=DC,∠BAC=80°,则∠BAD=__________,∠CDA=__________.
11.
如图所示,P在∠AOB的平分线上,在利用角平分线性质推证PD=PE时,必须满足的条件是____________________.
12.
如图所示,∠B=∠C,AB=AC,BD=DC,则要证明AD是∠BAC的__________线.需要通过__________来证明.如果在已知条件中增加∠B与∠C互补后,就可以通过__________来证明.因为此时BD与DC已经分别是__________的距离.
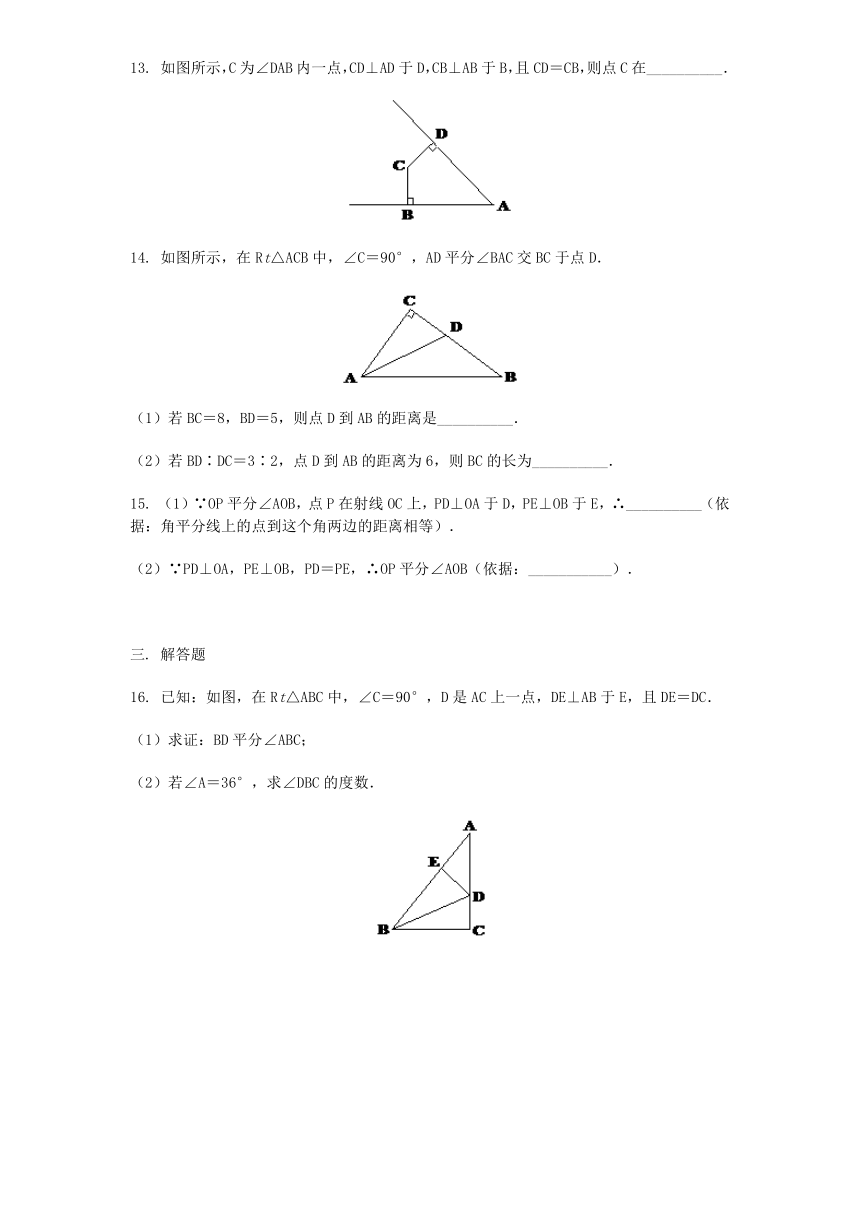
13.
如图所示,C为∠DAB内一点,CD⊥AD于D,CB⊥AB于B,且CD=CB,则点C在__________.
14.
如图所示,在Rt△ACB中,∠C=90°,AD平分∠BAC交BC于点D.
(1)若BC=8,BD=5,则点D到AB的距离是__________.
(2)若BD∶DC=3∶2,点D到AB的距离为6,则BC的长为__________.
15.
(1)∵OP平分∠AOB,点P在射线OC上,PD⊥OA于D,PE⊥OB于E,∴__________(依据:角平分线上的点到这个角两边的距离相等).
(2)∵PD⊥OA,PE⊥OB,PD=PE,∴OP平分∠AOB(依据:___________).
三.
解答题
16.
已知:如图,在Rt△ABC中,∠C=90°,D是AC上一点,DE⊥AB于E,且DE=DC.
(1)求证:BD平分∠ABC;
(2)若∠A=36°,求∠DBC的度数.
17.
如图:△ABC中,AD是∠BAC的平分线,E、F分别为AB、AC上的点,且∠EDF+∠BAF=180°.
(1)求证:DE=DF;
(2)若把最后一个条件改为:AE>AF,且∠AED+∠AFD=180°,那么结论还成立吗?
18.
如图,∠1=∠2,AE⊥OB于E,BD⊥OA于D,AE与BD相交于点C.求证:AC=BC.
19.
如图所示,某铁路MN与公路PQ相交于点O,且夹角为90°,其仓库G在A区,到公路和铁路距离相等,且到铁路图上距离为1cm.
(1)在图上标出仓库G的位置.(比例尺为1∶10000,用尺规作图)
(2)求出仓库G到铁路的实际距离.
四.
探究题
20.
有位同学发现了“角平分线”的另一种尺规作法,其方法为:
(1)如图所示,以O为圆心,任意长为半径画弧交OM、ON于点A、B;
(2)以O为圆心,不等于(1)中的半径长为半径画弧交OM、ON于点C、D;
(3)连接AD、BC相交于点E;
(4)作射线OE,则OE为∠MON的平分线.
你认为他这种作法对吗?试说明理由.
参考答案
一.
选择题
1.
B??
2.
A??
3.
B??
4.
A??
5.
D??
6.
C??
7.
B??
8.
D
二.
填空题
9.
3cm
????????????
10.
40°,50°???????????
11.
PD⊥OA,PE⊥OB
12.
角平分,全等,角平分线的性质,点D到AB、AC两边
13.
∠DAB的角平分线上?
14.
(1)3(2)15
15.
(1)PD=PE(2)到角的两边距离相等的点在角的平分线上
三.
解答题
16.
(1)证明:∵DC⊥BC,DE⊥AB,DE=DC,
∴点D在∠ABC的平分线上,∴BD平分∠ABC.
(2)∵∠C=90°,∠A=36°,∴∠ABC=54°,
∵BD平分∠ABC,∴∠DBC=∠ABC=27°.
17.
(1)证明:作DM⊥AB于M,DN⊥AC于N,
又∵AD平分∠BAC,∴DM=DN,
∵∠EAF+∠EDF=180°,∴∠AED+∠AFD=360°-180°=180°,
∵∠AFD+∠CFD=180°,∴∠AED=∠CFD,
∴△DME≌△DNF,∴DE=DF.
(2)仍成立.
18.
证明:∵∠1=∠2,BD⊥OA,AE⊥OB,
∴CD=CE,
∵∠DCA=∠ECB,∠ADC=∠BEC=90°,
∴△ACD≌△BCE,
∴AC=BC.
19.
(1)图略,仓库G在∠NOQ的平分线上,
(2)仓库G到铁路的实际距离是100m.
四.
探究题
20.
他这种作法对,理由如下:
由作法可知:OC=OD,OB=OA,∠COB=∠DOA,
∴△BCO≌△ADO,AC=BD,
∴∠OCE=∠ODE,
∵∠AEC=∠BED,
∴△ACE≌△BDE,
∴CE=DE,
∵OE=OE,
∴△OCE≌△ODE,
∴∠COE=∠DOE,即OE平分∠MON.
PAGE
同步检测题
一.
选择题
1.
如图所示,OP平分∠AOB,PC⊥OA于C,PD⊥OB于D,则PC与PD的大小关系是(??
)
A.
PC>PD???????????
B.
PC=PD?????????????
C.
PC<PD????????
D.
不能确定
2.
在Rt△ABC中,∠C=90°,AD是角平分线,若BC=10,BD∶CD=3∶2,则点D到AB的距离是(??
)
A.
4???????????????
B.
6???????????
C.
8????????????????D.
10
3.
在△ABC中,∠C=90°,E是AB边的中点,BD是角平分线,且DE⊥AB,则(??
)
A.
BC>AE???????????
B.
BC=AE????????????
C.
BC<AE?????????
D.
以上都有可能
4.
如图所示,点P是∠BAC的平分线AD上一点,PE⊥AC于点E,已知PE=3,则点P到AB的距离是(??
)
A.
3?????????????????????
B.
4?????????????
C.
5?????????????????????
D.
6
5.
如图所示,在△ABC中,∠C=90°,AD平分∠BAC,AE=AC,下列结论中错误的是(??
)
A.
DC=DE???????????
B.
∠AED=90°???
C.
∠ADE=∠ADC??
D.
DB=DC
6.
到三角形三边距离相等的点是(??
)
A.
三条高的交点???????????B.
三条中线的交点
C.
三条角平分线的交点????????D.
不能确定
7.
如图所示,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6cm,则△DEB的周长为(??
)
A.
4cm??????????????B.
6cm???????????????????
C.
10cm??????????????
D.
以上都不对
8.
如图所示,三条公路两两相交,交点分别为A、B、C,现计划修一个油库,要求到三条公路的距离相等,可供选择的地址有(??
)
A.
一处????????????
B.
二处?????????????????
C.
三处????????????D.
四处
二.
填空题
9.
如图所示,点P是∠CAB的平分线上一点,PF⊥AB于点F,PE⊥AC于点E,如果PF=3cm,那么PE=__________.
10.
如图所示,DB⊥AB,DC⊥AC,BD=DC,∠BAC=80°,则∠BAD=__________,∠CDA=__________.
11.
如图所示,P在∠AOB的平分线上,在利用角平分线性质推证PD=PE时,必须满足的条件是____________________.
12.
如图所示,∠B=∠C,AB=AC,BD=DC,则要证明AD是∠BAC的__________线.需要通过__________来证明.如果在已知条件中增加∠B与∠C互补后,就可以通过__________来证明.因为此时BD与DC已经分别是__________的距离.
13.
如图所示,C为∠DAB内一点,CD⊥AD于D,CB⊥AB于B,且CD=CB,则点C在__________.
14.
如图所示,在Rt△ACB中,∠C=90°,AD平分∠BAC交BC于点D.
(1)若BC=8,BD=5,则点D到AB的距离是__________.
(2)若BD∶DC=3∶2,点D到AB的距离为6,则BC的长为__________.
15.
(1)∵OP平分∠AOB,点P在射线OC上,PD⊥OA于D,PE⊥OB于E,∴__________(依据:角平分线上的点到这个角两边的距离相等).
(2)∵PD⊥OA,PE⊥OB,PD=PE,∴OP平分∠AOB(依据:___________).
三.
解答题
16.
已知:如图,在Rt△ABC中,∠C=90°,D是AC上一点,DE⊥AB于E,且DE=DC.
(1)求证:BD平分∠ABC;
(2)若∠A=36°,求∠DBC的度数.
17.
如图:△ABC中,AD是∠BAC的平分线,E、F分别为AB、AC上的点,且∠EDF+∠BAF=180°.
(1)求证:DE=DF;
(2)若把最后一个条件改为:AE>AF,且∠AED+∠AFD=180°,那么结论还成立吗?
18.
如图,∠1=∠2,AE⊥OB于E,BD⊥OA于D,AE与BD相交于点C.求证:AC=BC.
19.
如图所示,某铁路MN与公路PQ相交于点O,且夹角为90°,其仓库G在A区,到公路和铁路距离相等,且到铁路图上距离为1cm.
(1)在图上标出仓库G的位置.(比例尺为1∶10000,用尺规作图)
(2)求出仓库G到铁路的实际距离.
四.
探究题
20.
有位同学发现了“角平分线”的另一种尺规作法,其方法为:
(1)如图所示,以O为圆心,任意长为半径画弧交OM、ON于点A、B;
(2)以O为圆心,不等于(1)中的半径长为半径画弧交OM、ON于点C、D;
(3)连接AD、BC相交于点E;
(4)作射线OE,则OE为∠MON的平分线.
你认为他这种作法对吗?试说明理由.
参考答案
一.
选择题
1.
B??
2.
A??
3.
B??
4.
A??
5.
D??
6.
C??
7.
B??
8.
D
二.
填空题
9.
3cm
????????????
10.
40°,50°???????????
11.
PD⊥OA,PE⊥OB
12.
角平分,全等,角平分线的性质,点D到AB、AC两边
13.
∠DAB的角平分线上?
14.
(1)3(2)15
15.
(1)PD=PE(2)到角的两边距离相等的点在角的平分线上
三.
解答题
16.
(1)证明:∵DC⊥BC,DE⊥AB,DE=DC,
∴点D在∠ABC的平分线上,∴BD平分∠ABC.
(2)∵∠C=90°,∠A=36°,∴∠ABC=54°,
∵BD平分∠ABC,∴∠DBC=∠ABC=27°.
17.
(1)证明:作DM⊥AB于M,DN⊥AC于N,
又∵AD平分∠BAC,∴DM=DN,
∵∠EAF+∠EDF=180°,∴∠AED+∠AFD=360°-180°=180°,
∵∠AFD+∠CFD=180°,∴∠AED=∠CFD,
∴△DME≌△DNF,∴DE=DF.
(2)仍成立.
18.
证明:∵∠1=∠2,BD⊥OA,AE⊥OB,
∴CD=CE,
∵∠DCA=∠ECB,∠ADC=∠BEC=90°,
∴△ACD≌△BCE,
∴AC=BC.
19.
(1)图略,仓库G在∠NOQ的平分线上,
(2)仓库G到铁路的实际距离是100m.
四.
探究题
20.
他这种作法对,理由如下:
由作法可知:OC=OD,OB=OA,∠COB=∠DOA,
∴△BCO≌△ADO,AC=BD,
∴∠OCE=∠ODE,
∵∠AEC=∠BED,
∴△ACE≌△BDE,
∴CE=DE,
∵OE=OE,
∴△OCE≌△ODE,
∴∠COE=∠DOE,即OE平分∠MON.
PAGE
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
