湘教版七年级数学下册 第4章《相交线与平行线》单元测试(含答案)
文档属性
| 名称 | 湘教版七年级数学下册 第4章《相交线与平行线》单元测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 202.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 16:55:32 | ||
图片预览



文档简介
第四章
相交线与平行线单元测试题
班级
姓名
总分
1、
选择题(本题共10小题,每小题4分,共40分)
1.下列各图中,∠1与∠2是对顶角的是(
)
2.如图,AB∥CD,∠A=50°,则∠1的大小是(
)
A.50°
B.120°
C.130°
D.150°
3.下面的每组图形中,左边的平移后可以得到右边的是(
)
4.如图,已知∠1=∠2=∠4,则下列结论不正确的是(
)
A.∠3=∠5
B.∠4=∠6
C.AD∥BC
D.AB∥CD
5.若a⊥b,c∥b,则a与c的关系是(
)
A.平行
B.垂直
C.相交
D.以上都不对
6.某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是(
)
A.甲种方案所用铁丝最长
B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长
D.三种方案所用铁丝一样长
7.如图所示,P为直线m外一点,点A,B,C在直线m上,且PB⊥m,垂足为B,∠APC=90°,则下列说法错误的是(
)
A.线段PB的长度叫做点P到直线m的距离
B.PA,PB,PC三条线段中,PB最短
C.线段AC的长度等于点P到直线m的距离
D.线段PA的长度叫做点A到直线PC的距离
8.如图,直线AB∥CD,∠C=44°,∠E=90°,则∠1等于(
)
A.
132°
B.134°
C.136°
D.138°
9.
如图,中,,过点且
平行于,若,则的度数为(
)
A.
B.
C.
D.
10.
如图,已知AC∥BD,∠CAE=30°,∠DBE=45°,则∠AEB等于(
)
A.30°
B.45°
C.60°
D.75°
二、填空题(本题共8小题,每小题4分,共32分)
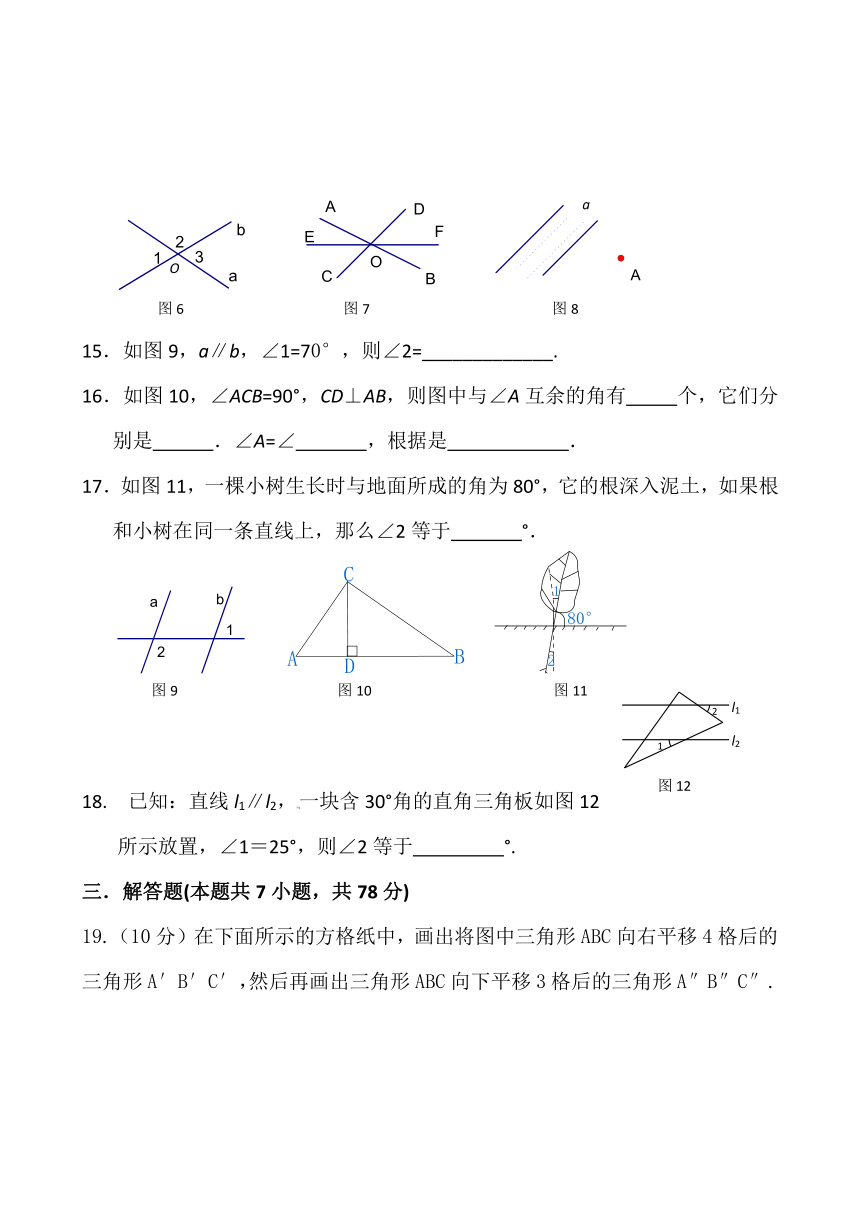
11.如图6,直线a,
b相交于点O,∠1=36°,则∠3=________,∠2=__________.
12.如图7,直线AB、CD、EF相交于点O,则∠AOC的对顶角是_____________,∠AOD的对顶角是_____________.
13.已知a、b、c是直线,若a∥b,b∥c,则a__
_c;若a⊥b,b⊥c,则a___c.
14.如图8,要从小河a引水到村庄A,请设计并作出一最短路线,画在图中,理由是:_____
_____.
15.如图9,a∥b,∠1=70°,则∠2=_____________.
16.如图10,∠ACB=90°,CD⊥AB,则图中与∠A互余的角有
个,它们分别是
.∠A=∠
,根据是
.
17.如图11,一棵小树生长时与地面所成的角为80°,它的根深入泥土,如果根和小树在同一条直线上,那么∠2等于
°.
18.
已知:直线l1∥l2,一块含30°角的直角三角板如图12
所示放置,∠1=25°,则∠2等于
°.
三.解答题(本题共7小题,共78分)
19.(10分)在下面所示的方格纸中,画出将图中三角形ABC向右平移4格后的三角形A′B′C′,然后再画出三角形ABC向下平移3格后的三角形A″B″C″.
20.(10分)如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
21.填写推理理由(10分)
(1)已知:如图,点D、E、F分别是边BC、AB、CA上的点,DF∥AB,DE∥AC,试说明∠FDE=∠A.
解:∵DF∥AB,(
)
∴∠A+∠AFD=1800.(
)
∵DE∥AC,(
)
∴∠AFD+∠EDF=1800.(
)
∴∠A=∠FDE.(
)
(2)如图AB∥CD
∠1=∠2,∠3=∠4,试说明AD∥BE.
解:∵AB∥CD(已知)
∴∠4=∠_____(
)
∵∠3=∠4(已知)
∴∠3=∠_____(
)
∵∠1=∠2(已知)
∴∠
1+∠CAF=∠2+∠CAF(
)
即
∠_____
=∠_____.
∴∠3=∠_____.
(
)
∴AD//EB.(
)
22.(10分)如图,已知点E,F分别在BA,CD的延长线上,连接EF,分别交AC,BD于点G,H,且∠1=∠2,∠B=∠C.
(1)AC与BD平行吗?为什么?
(2)BE与CF平行吗?为什么?
23.(10分)如图,在三角形ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC,试说明:∠1=∠2.
23(12分)
如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
24.(12分)如图,直线AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P,则∠EPF=90°吗?为什么?阅读下面解答过程,在括号内填写依据.
25.(10分)如图,在四边形ABCD中,AB∥CD,∠A=110°,∠ABC=∠ADC,BE平分∠ABC,与CD相交于点E,DF平分∠ADC,与AB相交于点F.
(1)试说明:BE∥DF;
(2)求∠BED的度数.
参考答案
(四)相交线与平行线
一、
选择题:
1.C
2.C
3.D
4.D
5.B
6.D
7.
C
8.B
9.
A
10
D
二、填空题:
11.36°,144°
12.
∠BOD,∠BOC
13.//,//
14.垂线段最短
15.
110°
16.2,∠ACD和∠B,BCD,同角的余角相等
17.10
18.35°
三、解答题:
19.
略
20
.解:因为AB∥CD,
所以∠ABC=∠1=65°,∠ABD+∠BDC=180°.
因为BC平分∠ABD,
所以∠ABD=2∠ABC=130°.
所以∠BDC=180°-∠ABD=50°.
所以∠2=∠BDC=50°.
21.
(1)已知;两直线平行,同旁内角互补;已知;两直线平行,同旁内角互补;同角的补角相等.
(2);两直线平行,同位角相等;;等量代换;等式的性质;;;等量代换;内错角相等,两直线平行.
20.72°,18°,162°.
22.解:(1)AC∥BD.
理由:因为∠1=∠CGF,∠1=∠2,
所以∠CGF=∠2.
所以AC∥BD(同位角相等,两直线平行).
(2)BE∥CF.
理由:因为AC∥BD,
所以∠B+∠BAC=180°.
因为∠B=∠C,
所以∠C+∠BAC=180°.
所以BE∥CF(同旁内角互补,两直线平行).
23解:因为CD⊥AB,FG⊥AB,
所以CD∥FG.
所以∠2=∠3.
因为DE∥BC,
所以∠1=∠3.
所以∠1=∠2.
24.解:∠EPF=90°.
理由:
过P作PG∥AB,因为AB∥CD(已知),
所以AB∥PG∥CD(两条直线都和第三条直线平行,那么这两条直线互相平行).
所以∠1=∠2,∠3=∠4,∠BEF+∠EFD=180°(两条直线平行,内错角相等,同旁内角互补).
又因为EP平分∠BEF,FP平分∠EFD(已知),
所以∠1=∠BEF,∠4=∠EFD(角平分线的定义).
所以∠EPF=∠2+∠3=∠1+∠4=∠BEF+∠EFD=(∠BEF+∠EFD)=×180°=90°.
25.解:(1)因为BE平分∠ABC,DF平分∠ADC,
所以∠FBE=∠ABC,∠FDE=∠ADC.
因为∠ABC=∠ADC,
所以∠FBE=∠FDE.
因为AB∥CD,
所以∠FBE+∠BED=180°.
所以∠FDE+∠BED=180°.
所以BE∥DF.
(2)因为AB∥CD,
所以∠A+∠ADC=180°.
因为∠A=110°,
所以∠ADC=70°.
所以∠FDE=∠ADC=35°.
因为BE∥DF,
所以∠BED=180°-∠FDE=145°.
图6
图7
图8
O
a
图9
图10
图11
l1
1
图12
l2
2
相交线与平行线单元测试题
班级
姓名
总分
1、
选择题(本题共10小题,每小题4分,共40分)
1.下列各图中,∠1与∠2是对顶角的是(
)
2.如图,AB∥CD,∠A=50°,则∠1的大小是(
)
A.50°
B.120°
C.130°
D.150°
3.下面的每组图形中,左边的平移后可以得到右边的是(
)
4.如图,已知∠1=∠2=∠4,则下列结论不正确的是(
)
A.∠3=∠5
B.∠4=∠6
C.AD∥BC
D.AB∥CD
5.若a⊥b,c∥b,则a与c的关系是(
)
A.平行
B.垂直
C.相交
D.以上都不对
6.某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是(
)
A.甲种方案所用铁丝最长
B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长
D.三种方案所用铁丝一样长
7.如图所示,P为直线m外一点,点A,B,C在直线m上,且PB⊥m,垂足为B,∠APC=90°,则下列说法错误的是(
)
A.线段PB的长度叫做点P到直线m的距离
B.PA,PB,PC三条线段中,PB最短
C.线段AC的长度等于点P到直线m的距离
D.线段PA的长度叫做点A到直线PC的距离
8.如图,直线AB∥CD,∠C=44°,∠E=90°,则∠1等于(
)
A.
132°
B.134°
C.136°
D.138°
9.
如图,中,,过点且
平行于,若,则的度数为(
)
A.
B.
C.
D.
10.
如图,已知AC∥BD,∠CAE=30°,∠DBE=45°,则∠AEB等于(
)
A.30°
B.45°
C.60°
D.75°
二、填空题(本题共8小题,每小题4分,共32分)
11.如图6,直线a,
b相交于点O,∠1=36°,则∠3=________,∠2=__________.
12.如图7,直线AB、CD、EF相交于点O,则∠AOC的对顶角是_____________,∠AOD的对顶角是_____________.
13.已知a、b、c是直线,若a∥b,b∥c,则a__
_c;若a⊥b,b⊥c,则a___c.
14.如图8,要从小河a引水到村庄A,请设计并作出一最短路线,画在图中,理由是:_____
_____.
15.如图9,a∥b,∠1=70°,则∠2=_____________.
16.如图10,∠ACB=90°,CD⊥AB,则图中与∠A互余的角有
个,它们分别是
.∠A=∠
,根据是
.
17.如图11,一棵小树生长时与地面所成的角为80°,它的根深入泥土,如果根和小树在同一条直线上,那么∠2等于
°.
18.
已知:直线l1∥l2,一块含30°角的直角三角板如图12
所示放置,∠1=25°,则∠2等于
°.
三.解答题(本题共7小题,共78分)
19.(10分)在下面所示的方格纸中,画出将图中三角形ABC向右平移4格后的三角形A′B′C′,然后再画出三角形ABC向下平移3格后的三角形A″B″C″.
20.(10分)如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
21.填写推理理由(10分)
(1)已知:如图,点D、E、F分别是边BC、AB、CA上的点,DF∥AB,DE∥AC,试说明∠FDE=∠A.
解:∵DF∥AB,(
)
∴∠A+∠AFD=1800.(
)
∵DE∥AC,(
)
∴∠AFD+∠EDF=1800.(
)
∴∠A=∠FDE.(
)
(2)如图AB∥CD
∠1=∠2,∠3=∠4,试说明AD∥BE.
解:∵AB∥CD(已知)
∴∠4=∠_____(
)
∵∠3=∠4(已知)
∴∠3=∠_____(
)
∵∠1=∠2(已知)
∴∠
1+∠CAF=∠2+∠CAF(
)
即
∠_____
=∠_____.
∴∠3=∠_____.
(
)
∴AD//EB.(
)
22.(10分)如图,已知点E,F分别在BA,CD的延长线上,连接EF,分别交AC,BD于点G,H,且∠1=∠2,∠B=∠C.
(1)AC与BD平行吗?为什么?
(2)BE与CF平行吗?为什么?
23.(10分)如图,在三角形ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC,试说明:∠1=∠2.
23(12分)
如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
24.(12分)如图,直线AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P,则∠EPF=90°吗?为什么?阅读下面解答过程,在括号内填写依据.
25.(10分)如图,在四边形ABCD中,AB∥CD,∠A=110°,∠ABC=∠ADC,BE平分∠ABC,与CD相交于点E,DF平分∠ADC,与AB相交于点F.
(1)试说明:BE∥DF;
(2)求∠BED的度数.
参考答案
(四)相交线与平行线
一、
选择题:
1.C
2.C
3.D
4.D
5.B
6.D
7.
C
8.B
9.
A
10
D
二、填空题:
11.36°,144°
12.
∠BOD,∠BOC
13.//,//
14.垂线段最短
15.
110°
16.2,∠ACD和∠B,BCD,同角的余角相等
17.10
18.35°
三、解答题:
19.
略
20
.解:因为AB∥CD,
所以∠ABC=∠1=65°,∠ABD+∠BDC=180°.
因为BC平分∠ABD,
所以∠ABD=2∠ABC=130°.
所以∠BDC=180°-∠ABD=50°.
所以∠2=∠BDC=50°.
21.
(1)已知;两直线平行,同旁内角互补;已知;两直线平行,同旁内角互补;同角的补角相等.
(2);两直线平行,同位角相等;;等量代换;等式的性质;;;等量代换;内错角相等,两直线平行.
20.72°,18°,162°.
22.解:(1)AC∥BD.
理由:因为∠1=∠CGF,∠1=∠2,
所以∠CGF=∠2.
所以AC∥BD(同位角相等,两直线平行).
(2)BE∥CF.
理由:因为AC∥BD,
所以∠B+∠BAC=180°.
因为∠B=∠C,
所以∠C+∠BAC=180°.
所以BE∥CF(同旁内角互补,两直线平行).
23解:因为CD⊥AB,FG⊥AB,
所以CD∥FG.
所以∠2=∠3.
因为DE∥BC,
所以∠1=∠3.
所以∠1=∠2.
24.解:∠EPF=90°.
理由:
过P作PG∥AB,因为AB∥CD(已知),
所以AB∥PG∥CD(两条直线都和第三条直线平行,那么这两条直线互相平行).
所以∠1=∠2,∠3=∠4,∠BEF+∠EFD=180°(两条直线平行,内错角相等,同旁内角互补).
又因为EP平分∠BEF,FP平分∠EFD(已知),
所以∠1=∠BEF,∠4=∠EFD(角平分线的定义).
所以∠EPF=∠2+∠3=∠1+∠4=∠BEF+∠EFD=(∠BEF+∠EFD)=×180°=90°.
25.解:(1)因为BE平分∠ABC,DF平分∠ADC,
所以∠FBE=∠ABC,∠FDE=∠ADC.
因为∠ABC=∠ADC,
所以∠FBE=∠FDE.
因为AB∥CD,
所以∠FBE+∠BED=180°.
所以∠FDE+∠BED=180°.
所以BE∥DF.
(2)因为AB∥CD,
所以∠A+∠ADC=180°.
因为∠A=110°,
所以∠ADC=70°.
所以∠FDE=∠ADC=35°.
因为BE∥DF,
所以∠BED=180°-∠FDE=145°.
图6
图7
图8
O
a
图9
图10
图11
l1
1
图12
l2
2
