苏科版九年级数学中考复习导学案——辅助线专题(答案不全)
文档属性
| 名称 | 苏科版九年级数学中考复习导学案——辅助线专题(答案不全) |  | |
| 格式 | zip | ||
| 文件大小 | 411.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 23:52:32 | ||
图片预览

文档简介
九年级数学中考复习导学案(辅助线专题)
教学目标:复习数学解题常用的辅助线方法,增强解题能力。
教学过程:
一、常见的辅助线方法:
1、连接(知中垂,连两端,距离等);
2、延长;
3、作垂线(如:知平分,向两边,作垂
直);
4、作平行
线;
5、倍长中线法;
6、截长补短法;
7、平移法;
8、旋转法;
9、构造法(如:见中点再取中点,构造=中位线;见中线延长一倍,构造平行四边形);
二.基本图形的辅助线的画法
三角形中常见辅助线的添加
1.
与角平分线有关的
已知P是∠MON平分线上一点,
垂直:若PA⊥OM于点A,如图a,可以过P点作PB⊥ON于点B,则PB=PA。可记为“图中有角平分线,可向两边作垂线”。
截取:若点A是射线OM上任意一点,如图b,可以在ON上截取OB=OA,连接PB,构造△OPB≌△OPA。可记为“图中有角平分线,可以将图形对折看,对称以后关系现”。
等腰:若AP⊥OP于点P,如图c,可延长AP交ON于点B,构造△AOB是等腰三角形,P是底边AB的中点,可记为“角平分线加垂线,三线合一试试看”。
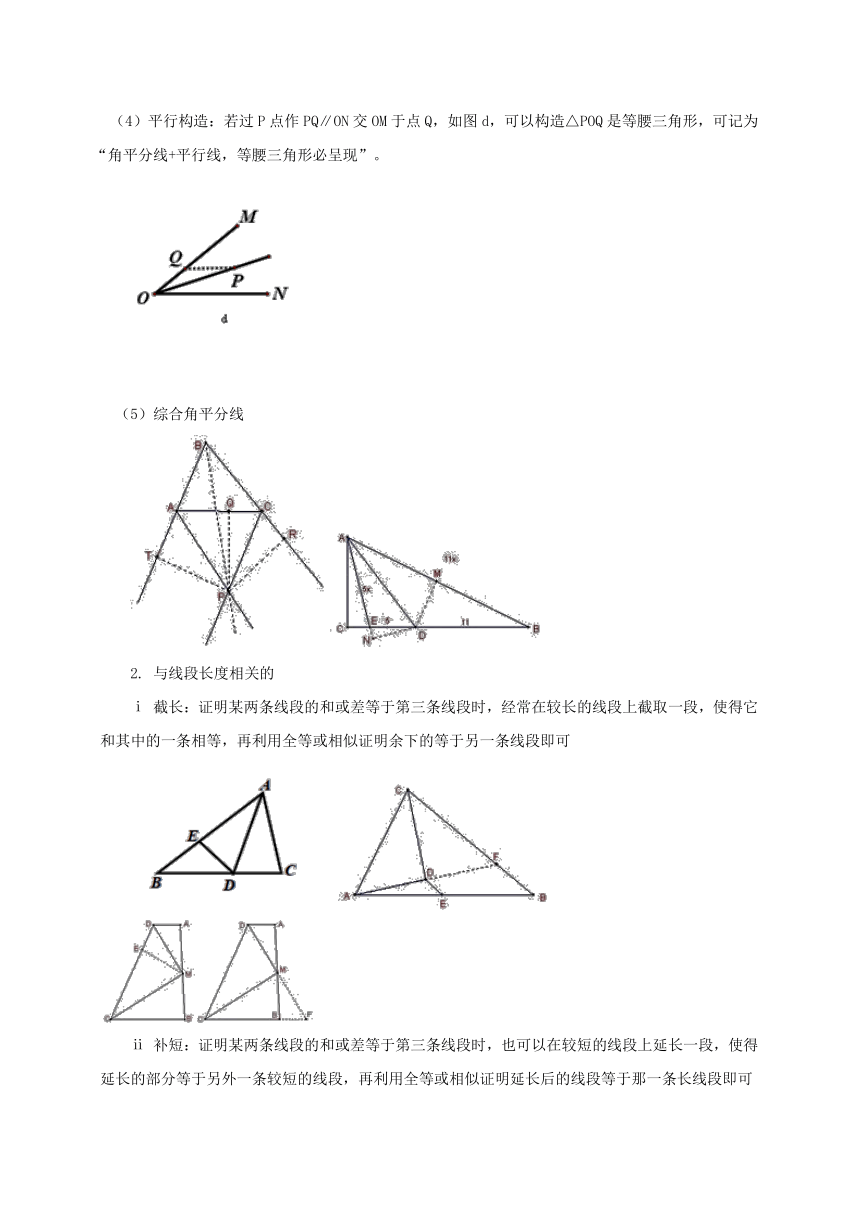
平行构造:若过P点作PQ∥ON交OM于点Q,如图d,可以构造△POQ是等腰三角形,可记为“角平分线+平行线,等腰三角形必呈现”。
(5)综合角平分线
2.
与线段长度相关的
ⅰ
截长:证明某两条线段的和或差等于第三条线段时,经常在较长的线段上截取一段,使得它和其中的一条相等,再利用全等或相似证明余下的等于另一条线段即可
ⅱ
补短:证明某两条线段的和或差等于第三条线段时,也可以在较短的线段上延长一段,使得延长的部分等于另外一条较短的线段,再利用全等或相似证明延长后的线段等于那一条长线段即可
ⅲ
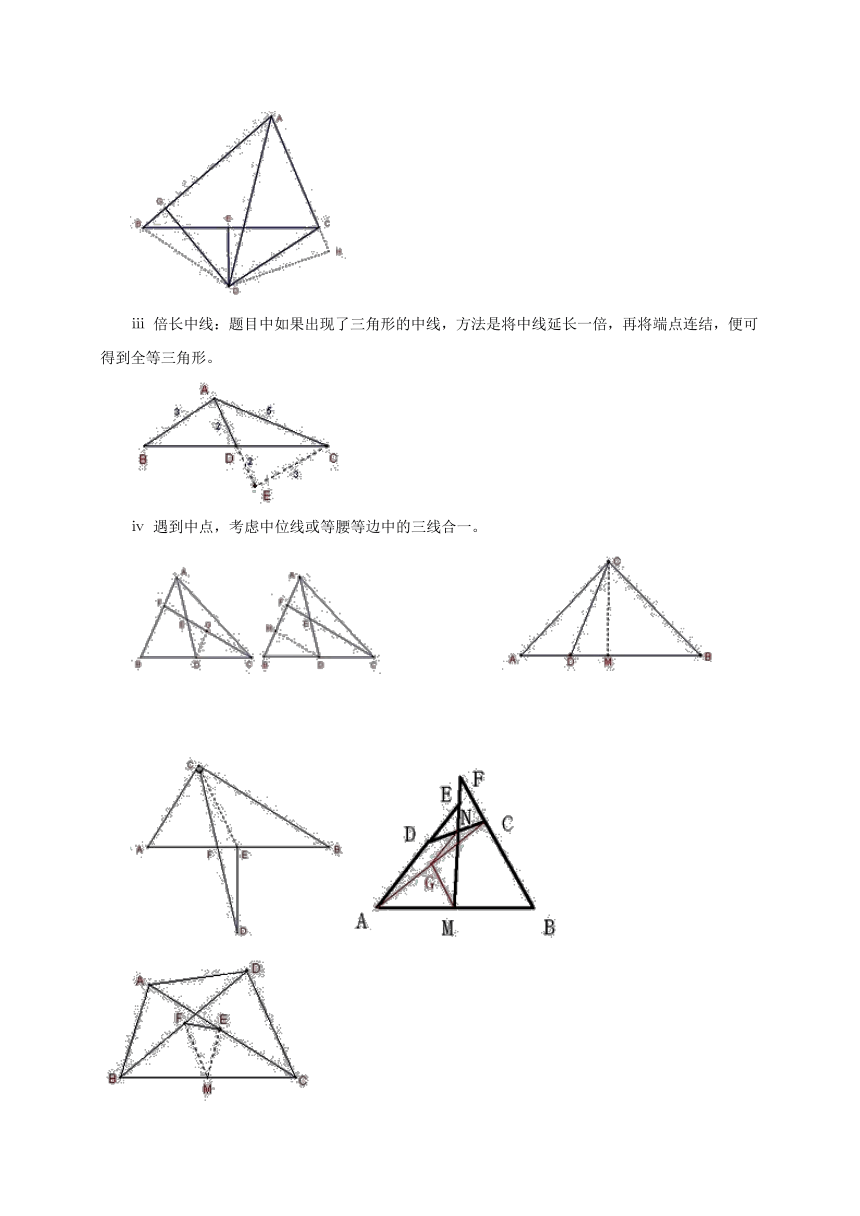
倍长中线:题目中如果出现了三角形的中线,方法是将中线延长一倍,再将端点连结,便可得到全等三角形。
ⅳ
遇到中点,考虑中位线或等腰等边中的三线合一。
3.
与等腰等边三角形相关的
ⅰ
考虑三线合一
ⅱ
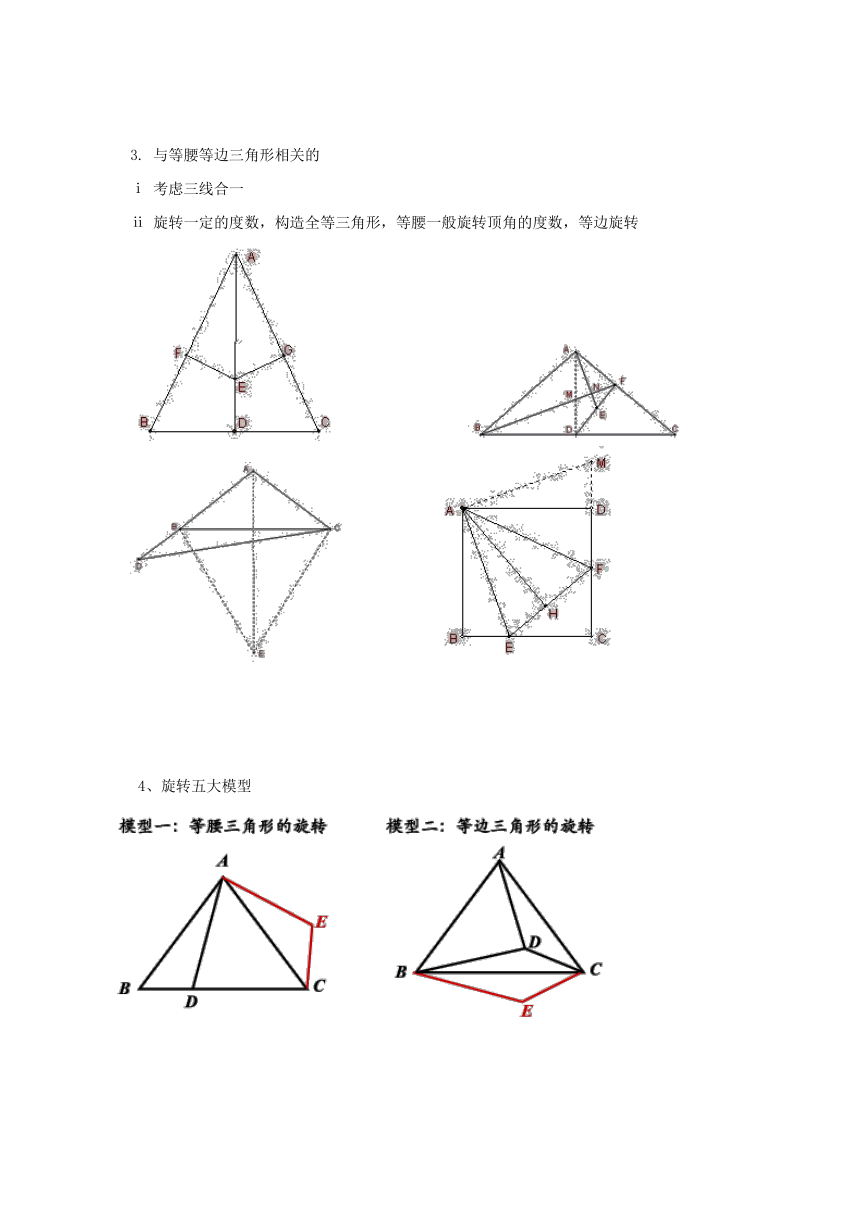
旋转一定的度数,构造全等三角形,等腰一般旋转顶角的度数,等边旋转
4、旋转五大模型
题型一:角平分线及截取
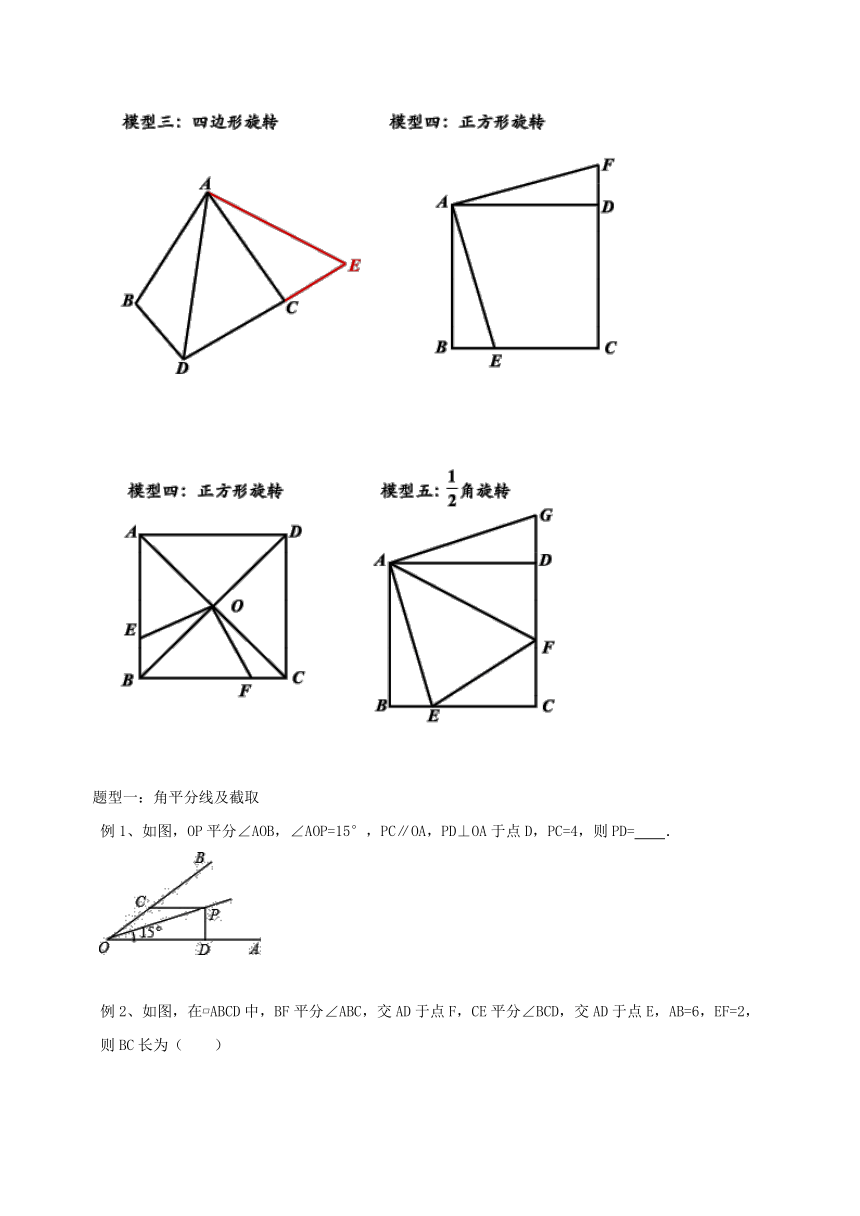
例1、如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=4,则PD= .
例2、如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )
例3、如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,过点C作CF⊥BE,垂足为F,连接OF,则OF的长为 .
例4、如图,BD是△ABC的角平分线,点E,F分别在BC、AB上,且DE∥AB,EF∥AC.
(1)求证:BE=AF;
(2)若∠ABC=60°,BD=6,求四边形ADEF的面积.
例5、
如图7,△ABC中,M是BC的中点,AD是∠A的平分线,BD⊥AD,垂足为D,AB=12,AC=18,求DM的长.
同步训练
1、如图,AD是△ABC的角平分线,则AB:AC等于( )
A.BD:CD
B.AD:CD
C.BC:AD
D.BC:AC
2、已知:如图,正方形ABCD,BM、DN分别平分正方形的两个外角,且满足∠MAN=45°,连结MN.
(1)若正方形的边长为a,求BM?DN的值.
(2)若以BM,DN,MN为三边围成三角形,试猜想三角形的形状,并证明你的结论.
题型二:中点、中线、垂直平分线
例1、如图,在Rt△ACB中,∠ACB=90°,AC=BC=3,CD=1,CH⊥BD于H,点O是AB中点,连接OH,则OH=
.
例2、爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AN⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
【特例探究】
(1)如图1,当tan∠PAB=1,c=4时,a= ,b= ;
如图2,当∠PAB=30°,c=2时,a=
,b=
;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
(3)如图4,?ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3,AB=3,求AF的长.
例3、如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.
(1)若∠B=60°,这时点P与点C重合,则∠NMP=
度;
(2)求证:NM=NP;
(3)当△NPC为等腰三角形时,求∠B的度数.
例4、已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.
(1)如图1,已知折痕与边BC交于点O,连结AP、OP、OA.
①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长;
(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;
(3)如图2,,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
题型三:旋转
例1、已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BP作垂线,垂足分别为点E、F,点O为AC的中点.
(1)当点P与点O重合时如图1,易证OE=OF(不需证明)
(2)直线BP绕点B逆时针方向旋转,当∠OFE=30°时,如图2、图3的位置,猜想线段CF、AE、OE之间有怎样的数量关系?请写出你对图2、图3的猜想,并选择一种情况给予证明.
课堂同步训练
1、如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)
(1)如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.
2、如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是(
)
A.2.5
B.
C.
D.2
3、如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为 .
4、在菱形ABCD和正三角形BGF中,∠ABC=60°,P是DF的中点,连接PG、PC.
(1)如图1,当点G在BC边上时,易证:PG=PC.(不必证明)
(2)如图2,当点F在AB的延长线上时,线段PC、PG有怎样的数量关系,写出你的猜想,并给与证明;
(3)如图3,当点F在CB的延长线上时,线段PC、PG又有怎样的数量关系,写出你的猜想(不必证明).
参考答案:
1、(1)DM⊥FM,DM=FM
(2)DM⊥FM,DM=FM
2、B
3、或
4、(2)PG=PC
(3)PG=PC
教学目标:复习数学解题常用的辅助线方法,增强解题能力。
教学过程:
一、常见的辅助线方法:
1、连接(知中垂,连两端,距离等);
2、延长;
3、作垂线(如:知平分,向两边,作垂
直);
4、作平行
线;
5、倍长中线法;
6、截长补短法;
7、平移法;
8、旋转法;
9、构造法(如:见中点再取中点,构造=中位线;见中线延长一倍,构造平行四边形);
二.基本图形的辅助线的画法
三角形中常见辅助线的添加
1.
与角平分线有关的
已知P是∠MON平分线上一点,
垂直:若PA⊥OM于点A,如图a,可以过P点作PB⊥ON于点B,则PB=PA。可记为“图中有角平分线,可向两边作垂线”。
截取:若点A是射线OM上任意一点,如图b,可以在ON上截取OB=OA,连接PB,构造△OPB≌△OPA。可记为“图中有角平分线,可以将图形对折看,对称以后关系现”。
等腰:若AP⊥OP于点P,如图c,可延长AP交ON于点B,构造△AOB是等腰三角形,P是底边AB的中点,可记为“角平分线加垂线,三线合一试试看”。
平行构造:若过P点作PQ∥ON交OM于点Q,如图d,可以构造△POQ是等腰三角形,可记为“角平分线+平行线,等腰三角形必呈现”。
(5)综合角平分线
2.
与线段长度相关的
ⅰ
截长:证明某两条线段的和或差等于第三条线段时,经常在较长的线段上截取一段,使得它和其中的一条相等,再利用全等或相似证明余下的等于另一条线段即可
ⅱ
补短:证明某两条线段的和或差等于第三条线段时,也可以在较短的线段上延长一段,使得延长的部分等于另外一条较短的线段,再利用全等或相似证明延长后的线段等于那一条长线段即可
ⅲ
倍长中线:题目中如果出现了三角形的中线,方法是将中线延长一倍,再将端点连结,便可得到全等三角形。
ⅳ
遇到中点,考虑中位线或等腰等边中的三线合一。
3.
与等腰等边三角形相关的
ⅰ
考虑三线合一
ⅱ
旋转一定的度数,构造全等三角形,等腰一般旋转顶角的度数,等边旋转
4、旋转五大模型
题型一:角平分线及截取
例1、如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=4,则PD= .
例2、如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )
例3、如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,过点C作CF⊥BE,垂足为F,连接OF,则OF的长为 .
例4、如图,BD是△ABC的角平分线,点E,F分别在BC、AB上,且DE∥AB,EF∥AC.
(1)求证:BE=AF;
(2)若∠ABC=60°,BD=6,求四边形ADEF的面积.
例5、
如图7,△ABC中,M是BC的中点,AD是∠A的平分线,BD⊥AD,垂足为D,AB=12,AC=18,求DM的长.
同步训练
1、如图,AD是△ABC的角平分线,则AB:AC等于( )
A.BD:CD
B.AD:CD
C.BC:AD
D.BC:AC
2、已知:如图,正方形ABCD,BM、DN分别平分正方形的两个外角,且满足∠MAN=45°,连结MN.
(1)若正方形的边长为a,求BM?DN的值.
(2)若以BM,DN,MN为三边围成三角形,试猜想三角形的形状,并证明你的结论.
题型二:中点、中线、垂直平分线
例1、如图,在Rt△ACB中,∠ACB=90°,AC=BC=3,CD=1,CH⊥BD于H,点O是AB中点,连接OH,则OH=
.
例2、爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AN⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
【特例探究】
(1)如图1,当tan∠PAB=1,c=4时,a= ,b= ;
如图2,当∠PAB=30°,c=2时,a=
,b=
;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
(3)如图4,?ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3,AB=3,求AF的长.
例3、如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.
(1)若∠B=60°,这时点P与点C重合,则∠NMP=
度;
(2)求证:NM=NP;
(3)当△NPC为等腰三角形时,求∠B的度数.
例4、已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.
(1)如图1,已知折痕与边BC交于点O,连结AP、OP、OA.
①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长;
(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;
(3)如图2,,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
题型三:旋转
例1、已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BP作垂线,垂足分别为点E、F,点O为AC的中点.
(1)当点P与点O重合时如图1,易证OE=OF(不需证明)
(2)直线BP绕点B逆时针方向旋转,当∠OFE=30°时,如图2、图3的位置,猜想线段CF、AE、OE之间有怎样的数量关系?请写出你对图2、图3的猜想,并选择一种情况给予证明.
课堂同步训练
1、如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)
(1)如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.
2、如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是(
)
A.2.5
B.
C.
D.2
3、如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为 .
4、在菱形ABCD和正三角形BGF中,∠ABC=60°,P是DF的中点,连接PG、PC.
(1)如图1,当点G在BC边上时,易证:PG=PC.(不必证明)
(2)如图2,当点F在AB的延长线上时,线段PC、PG有怎样的数量关系,写出你的猜想,并给与证明;
(3)如图3,当点F在CB的延长线上时,线段PC、PG又有怎样的数量关系,写出你的猜想(不必证明).
参考答案:
1、(1)DM⊥FM,DM=FM
(2)DM⊥FM,DM=FM
2、B
3、或
4、(2)PG=PC
(3)PG=PC
同课章节目录
