专题10:直角三角形的存在性问题探究学案
文档属性
| 名称 | 专题10:直角三角形的存在性问题探究学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 460.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 00:00:00 | ||
图片预览




文档简介
专题十:直角三角形的存在性问题探究
(
专题导入
)
引例.如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=-x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若△ABD恰为等腰直角三角形,则b的值为
.
(
方法点睛
)
是否存在一点,使之与另外两个定点构成直角三角形的问题:首先弄清题意,注意区分直角顶点;其次借助于动点所在图形的解析式,表示出动点的坐标;然后按分类的情况,利用几何知识建立方程(组),求出动点坐标,注意要根据题意舍去不符合题意的点.
解决方法如下
方法一:利用勾股定理进行边长的计算,从而来解决问题;
方法二:往往可以利用到一线等三角之K字(90°)类型和母子相似型类型,尝试建构相应的相似来进行处理;
方法三:可利用直径所对的圆周角为90°来处理.
导例解析:分三种情况讨论:①当∠ABD=90°时,如图1,b=;②当∠ADB=90°时,如图2,b=;③当∠DAB=90°时,如图3,b=2
(
典例精讲
)
类型一:利用勾股定理来解决直角三角形的存在性问题
例1.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,与x轴的另一个交点为B.
(1)若直线y=mx+n经过B,C两点,求抛物线和直线BC的解析式;
(2)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
第2题图
【分析】(1)首先由题意,根据抛物线的对称称轴公式,待定系数法,建立关于a,b,c的方程组,解方程组可得答案;
(2)首先利用勾股这事不师古求得BC,PB,PC的长,然后分别从点B为直角顶点,点C为直角顶点,点P为直角顶点去分析求得答案.
类型二:构造相似来解决直角三角形存在性问题
例2.如图①,抛物线y=-x2+bx+8与x轴交于点A(-6,0),点B(点A在点B左侧),与y轴交于点C,点P为线段AO上的一个动点,过点P作x轴的垂线l与抛物线交于点E,连接AE,EC.
(1)求抛物线的解析式及点C的坐标;
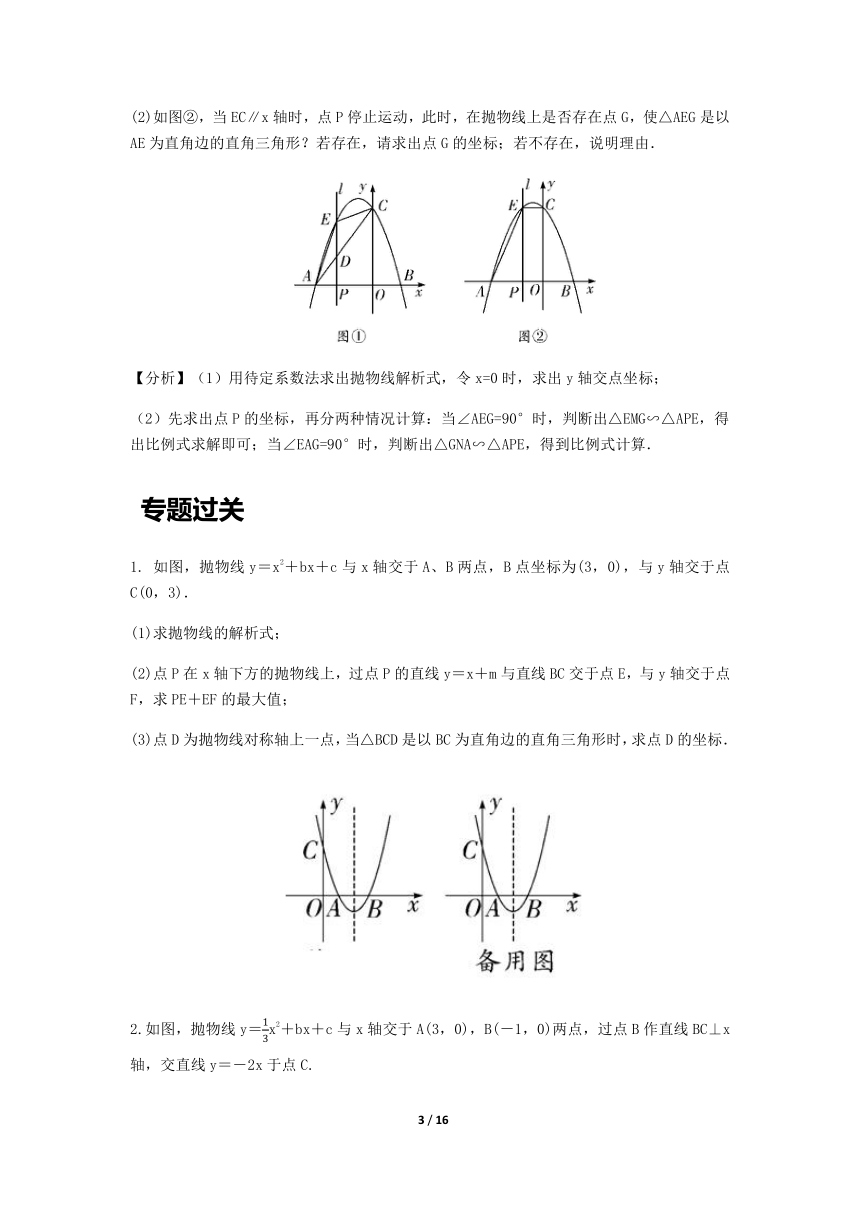
(2)如图②,当EC∥x轴时,点P停止运动,此时,在抛物线上是否存在点G,使△AEG是以AE为直角边的直角三角形?若存在,请求出点G的坐标;若不存在,说明理由.
【分析】(1)用待定系数法求出抛物线解析式,令x=0时,求出y轴交点坐标;
(2)先求出点P的坐标,再分两种情况计算:当∠AEG=90°时,判断出△EMG∽△APE,得出比例式求解即可;当∠EAG=90°时,判断出△GNA∽△APE,得到比例式计算.
(
专题过关
)
1.
如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值;
(3)点D为抛物线对称轴上一点,当△BCD是以BC为直角边的直角三角形时,求点D的坐标.
2.如图,抛物线y=x2+bx+c与x轴交于A(3,0),B(-1,0)两点,过点B作直线BC⊥x轴,交直线y=-2x于点C.
(1)求该抛物线的解析式;
(2)求该抛物线的顶点D的坐标,并判断顶点D是否在直线y=-2x上;
(3)点P是抛物线上一动点,是否存在这样的点P(点A除外),使△PBC是以BC为直角边的直角三角形?若存在,求出所有满足条件的点P的坐标;若不存在,请说明理由.
3.如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,直接写出符合条件的点P的坐标;若不存在,请说明理由;
4.如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B的坐标为(1,0),抛物线y=-x2+bx+c经过A,B两点.
(1)求抛物线的解析式;
(2)点P是直线AB上方抛物线上的一点.过点P作PD垂直x轴于点D,交线段AB于点E,使PE=DE.
①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.
5.已知抛物线y=ax2+bx+c的顶点坐标为P(2,4).
(1)试写出b,c之间的关系式;
(2)当a>0时,若一次函数y=x+4的图象与y轴及该抛物线的交点依次为D,E,F,且E,F的横坐标x1与x2之间满足关系x2=6x1.
①求△ODE与△OEF的面积比;
②是否存在a,使得∠EPF=90°?若存在,求出a的值;若不存在,请说明理由.
6.已知开口向下的抛物线y=ax2﹣2ax+3与x轴的交点为A,B两点(点A在点B的左边),与y轴的交点为C,OC=3OA.
(1)请直接写出该抛物线解析式;
(2)如图,D为抛物线的顶点,连接BD,BC,P为对称轴右侧抛物线上一点.若∠ABD=∠BCP,求点P的坐标
(3)在(2)的条件下,M,N是抛物线上的动点.若∠MPN=90°,直线MN必过一定点,请求出该定点的坐标.
答案
例1.
(1)由题意得,解得
∴抛物线的解析式为y=-x2-2x+3.
∵对称轴为直线x=-1,抛物线经过A(1,0),∴B(-3,0).
设直线BC的解析式y=mx+n,把B(-3,0),C(0,3)分别代入y=mx+n,得解得∴直线BC的解析式为y=x+3.∴M(-1,2);
(2)设P(-1,t),∵B(-3,0),C(0,3),∴BC2=18,
PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10.
①若B为直角顶点,则BC2+PB2=PC2,即18+4+t2=t2-6t+10,解得t=-2;
②若C为直角顶点,则BC2+PC2=PB2,即18+t2-6t+10=4+t2,解得t=4;
③若P为直角顶点,则PB2+PC2=BC2,即4+t2+t2-6t+10=18,解得t1=,t2=.
综上所述,满足条件的点P共有四个,分别为:P1(-1,-2),P2(-1,4),P3(-1,),P4(-1,).
例2(1)∵点A(-6,0)在抛物线y=-x2+bx+8上,
∴0=-×(-6)2+(-6b)+8,解得b=-.
∴抛物线的解析式为y=-x2-x+8,令x=0,得y=8,∴C(0,8);
(2))存在.如图①,连接EG,AG,过点G作GM⊥l,GN⊥x轴,垂足分别为M,N,
图①
∵EC∥x轴,∴EP=CO=8.把y=8代入y=-x2-x+8,则8=-x2-x+8,解得x=0(舍去)或x=-2.∴P(-2,0)
.∴AP=AO-PO=4.
(ⅰ)如图①,当∠AEG=90°时,∵∠MEG+∠AEP=90°,∠AEP+∠EAP=90°,
∴∠MEG=∠EAP.又∵∠APE=∠EMG=90°,
∴△EMG∽△APE.∴=.设点G(m,-m2-m+8)(m>0),
则GN=MP=-m2-m+8.∴EM=EP-MP=8-(-m2-m+8)=m2+m,
MG=PN=PO+ON=2+m.
∴==,∴m=-2(舍去)或m=.∴G(,);
(ⅱ)如图②,当∠EAG=90°时,
图②
∵∠NAG+∠EAP=90°,∠AEP+∠EAP=90°,
∴∠NAG=∠AEP.∵∠APE=∠GNA=90°,∴△GNA∽△APE.∴=.
设点G(n,-
n2-n+8)(n>4),∴GN=n2+n-8,AN=AO+ON=6+n.
∴=.∴n=-6(舍去)或n=.∴G(,-)
.
综上,符合条件的G点的坐标为(,)或(,-).
(
专题过关
)
1.(1)由题意得,解得∴抛物线的解析式为y=x2-4x+3;
(2)如图①,过点P作PG∥CF交CB与点G.
图①
由题可知,直线BC的解析式为y=-x+3,OC=OB=3,∴∠OCB=45°.同理可知∠OFE=45°.∴△CEF为等腰直角三角形.∵PG∥CF,∴△GPE为等腰直角三角形.
∵F(0,m),C(0,3),∴CF=3-m.∵△CEF∽△GEP,∴EF=CF=
(3-m),
PE=PG.
设P(t,t2-4t+3)(1则G(t,-t+3)PE=PG=
(-t+3-t-m)=
(-m-2t+3)
.
∵点P是直线y=x+m与抛物线的交点,∴t2-4t+3=t+m.
∴PE+EF=
(3-m)+
(-m-2t+3)=
(-2t-2m+6)=-
(t+m-3)=-
(t2-4t)=
-
(t-2)2+4.
∴当t=2时,PE+EF最大,最大值为4;
(3)由(1)知对称轴x=2,设点D(2,n),如图②.
图②
当△BCD是以BC为直角边的直角三角形时,分两种情况讨论:
(ⅰ)D在C上方D1位置时,由勾股定理得CD12+BC2=BD12,即(2-0)2+(n-3)2+(3)2=(3-2)2+(0-n)2
,解得n=5;
(ⅱ)D在C下方D2位置时,由勾股定理得BD22+BC2=CD22
即(2-3)2+(n-0)2+(3)2=(2-0)2+(n-3)2
,解得n=-1,
综上所述,当△BCD是以BC为直角边的直角三角形时,D为(2,5)或(2,-1).
2.:(1)∵y=x2+bx+c与x轴交于A(3,0),B(-1,0)两点,
∴解得,∴抛物线的解析式为y=x2-x-1;
(2)由y=x2-x-1=(x-1)2-,∴抛物线的顶点D的坐标为(1,-).
把x=1代入y=-2x中得y=-2.
∵-≠-2,∴顶点D不在直线y=-2x上;
(3)存在.理由如下:如图,过点C作x轴的平行线,与该抛物线交于点P1,P2,连接BP1,BP2.
∵直线BC⊥x轴,∴△P1BC、△P2BC都是直角三角形.
把x=-1代入y=-2x中得y=-2×(-1)=2.∴C(-1,2).
∴把y=2代入y=x2-x-1中,得x2-x-1=2,
解得x1=+1,x2=-+1.∴P1(+1,2),P2(-+1,2).
3.
(1)设抛物线解析式为y=a(x+1)(x-3),即y=ax2-2ax-3a.
∴-2a=2,解得a=-1,∴抛物线解析式为y=-x2+2x+3.
当x=0时,y=-x2+2x+3=3,则C(0,3).
设直线AC的解析式为y=px+q,
把A(-1,0),C(0,3)代入得解得∴直线AC的解析式为y=3x+3.
(2)∵y=-x2+2x+3=-(x-1)2+4,∴顶点D的坐标为(1,4).
如图,作B点关于y轴的对称点B′,则B′(-3,0),连接DB′交y轴于M.
∵MB=MB′,∴MB+MD=MB′+MD=DB′,此时MB+MD的值最小.
∵BD的值不变,∴此时△BDM的周长最小.易得直线DB′的解析式为y=x+3.
当x=0时,y=x+3=3,∴点M的坐标为(0,3).
(3)存在,符合条件的点P的坐标为(,)或(,-).
4.(1)在Rt△ABC中,由点B的坐标可知OB=1.
∵OC=2OB,∴OC=2,则BC=3.又∵tan∠ABC=2,
∴AC=2BC=6,则点A的坐标为(-2,6).
把点A,B的坐标代入抛物线y=-x2+bx+c中,得
解得∴该抛物线的解析式为y=-x2-3x+4.
(2)①由点A(-2,6)和点B(1,0)的坐标易得直线AB的解析式为y=-2x+2.
如图,设点P的坐标为(m,-m2-3m+4),则点E的坐标为(m,-2m+2),点D的坐标为(m,0)
.则PE=-m2-m+2,DE=-2m+2,
由PE=DE得-m2-m+2=(-2m+2),解得m=±1.
又∵-2<m<1,∴m=-1,∴点P的坐标为(-1,6).
②∵M在直线PD上,且P(-1,6),设M(-1,y),
∴AM2=(-1+2)2+(y-6)2=1+(y-6)2,BM2=(1+1)2+y2=4+y2,AB2=(1+2)2+62=45.
分三种情况:
(ⅰ)当∠AMB=90°时,有AM2+BM2=AB2,∴1+(y-6)2+4+y2=45,解得y=3±.
∴M(-1,3+)或(-1,3-);
(ⅱ)当∠ABM=90°时,有AB2+BM2=AM2,∴45+4+y2=1+(y-6)2,解得y=-1,∴M(-1,-1).
(ⅲ)当∠BAM=90°时,有AM2+AB2=BM2,
∴1+(y-6)2+45=4+y2,解得y=,∴M(-1,).
综上所述,点M的坐标为(-1,3+)或(-1,3-)或(-1,-1)或(-1,).
5.(1)∵抛物线顶点坐标为(2,4),
∴抛物线解析式为y=a(x﹣2)2+4=ax2﹣4ax+4a+4,
∴b=﹣4a,c=4a+4.∴b+c=4;
(2)①由题意可知△ODE和△ODF的底边DE、DF边上的高相同,
∴S△ODE:S△ODF=DE:DF=x1:x2=1:6.∴S△ODE:S△OEF=1:5;
②如图,分别过E,F作x轴的垂线,垂足分别为G、H,交直线DP于点M、N,
∵直线y=x+4,∴设点E坐标为(m,m+4),则点F的坐标为(6m,6m+4).
∴EM=EG﹣MG=m+4﹣4=m,FN=FH﹣NH=6m+4﹣4=6m,PM=PD﹣MD=2﹣m,PN=DN﹣PD=6m﹣2,
∵∠EPF=90°,∴∠EPM+∠FPN=90°,且∠FPN+∠PFN=90°.∴∠EPM=∠PFN.
∴△EPM∽△PEN.∴,即.整理可得6m2+7m+2=0,解得m=或m=,
当m=时,点E(,),F(3,7),把F点坐标代入抛物线解析式可得a+4=7,解得a=3,
∴抛物线解析式为y=3(x﹣2)2+4,当x=时,代入可求得y=≠,即点E不在该抛物线图象上,不符合题意.
当m=时,点E(,),F(4,8),把F点坐标代入抛物线解析式可求得a=1.
∴抛物线解析式为y=(x﹣2)2+4.
当x=时,代入可求得y=≠,即点E不在抛物线图象上,不符合题意,
综上可知不存在满足条件的a的值.
6.(1)当x=0时,y=ax2﹣2ax+3=3,
∴C(0,3),OC=3OA=3.∴OA=1,A(﹣1,0).
把点A(﹣1,0)代入抛物线解析式,得:a+2a+3=0,解得a=﹣1.
∴抛物线解析式为y=﹣x2+2x+3;
(2)如图1,若点P在抛物线对称轴右侧且在x轴上方,
过点P作PE∥y轴交BC于点E,PF⊥BC于点F,过点D作DH⊥x轴于点H,
∴∠CFP=∠BHD=90°.
∵当y=﹣x2+2x+3=0时,解得:x1=﹣1,x2=3.∴A(﹣1,0),B(3,0).
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点D(1,4).∴DH=4,BH=3﹣1=2.
∴BD=.
∴Rt△BDH中,sin∠ABD=.
∵C(0,3)∴BC=,PC=.
设直线BC解析式为y=kx+b,∴解得:,
∴直线BC解析式为y=﹣x+3.
设P(p,﹣p2+2p+3)(1<p<3),则E(p,﹣p+3),
∴PE=﹣p2+2p+3﹣(﹣p+3)=﹣p2+3p.
∵S△BCP=PE?OB=BC?PF,∴PF=.
∵∠ABD=∠BCP,∴Rt△CPF中,sin∠BCP==sin∠ABD=.
∴PF=PC.∴PF2=PC2.解得p1=﹣1(舍去),p2=.
∴﹣p2+2p+3=.∴点P坐标为(,).
如图2,若点P在x轴下方,
∵tan∠ABD==2>tan45°,∴∠ABD>45°.
∵∠BCP<∠BOC即∠BCP<45°,∴∠ABD与∠BCP不可能相等.
综上所述,点P坐标为(,);
(3)如图3,过P作PH∥y轴,分别过点M、N作MG⊥PH于G,NH⊥PH于H.
设直线MN的解析式为y=kx+n,M(x1,y1)、N(x2,y3),
令kx+n=﹣x2+2x+3,即=x2+(k﹣2)x+n﹣3=0,
∴x1+x2=2﹣k,x1x2=n﹣3.
∴y1+y2=k(x1+x2)+2n=k(2﹣k)+2n.
y1y2=(kx1+n)(kx2+n)=k2x1x2+nk(x1+x2)+n2=﹣3k2+2nk+n2,
∵∠G=∠MPN=∠H,∴△MPG∽△PNH.∴
.
∵P坐标为(,),MG=﹣x1,PH=y1﹣,HN=,GP=.
∴.整理,得.
∴.
解得
k1=﹣3n+,k2=.
∴直线MN;y=(﹣3n+)x+n=(﹣3x+1)n+,过定点(,);
或y=()x+n=()n+,过定点(,)即P点,舍去.
∴直线MN过定点(,).
16
/
16
(
专题导入
)
引例.如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=-x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若△ABD恰为等腰直角三角形,则b的值为
.
(
方法点睛
)
是否存在一点,使之与另外两个定点构成直角三角形的问题:首先弄清题意,注意区分直角顶点;其次借助于动点所在图形的解析式,表示出动点的坐标;然后按分类的情况,利用几何知识建立方程(组),求出动点坐标,注意要根据题意舍去不符合题意的点.
解决方法如下
方法一:利用勾股定理进行边长的计算,从而来解决问题;
方法二:往往可以利用到一线等三角之K字(90°)类型和母子相似型类型,尝试建构相应的相似来进行处理;
方法三:可利用直径所对的圆周角为90°来处理.
导例解析:分三种情况讨论:①当∠ABD=90°时,如图1,b=;②当∠ADB=90°时,如图2,b=;③当∠DAB=90°时,如图3,b=2
(
典例精讲
)
类型一:利用勾股定理来解决直角三角形的存在性问题
例1.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,与x轴的另一个交点为B.
(1)若直线y=mx+n经过B,C两点,求抛物线和直线BC的解析式;
(2)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
第2题图
【分析】(1)首先由题意,根据抛物线的对称称轴公式,待定系数法,建立关于a,b,c的方程组,解方程组可得答案;
(2)首先利用勾股这事不师古求得BC,PB,PC的长,然后分别从点B为直角顶点,点C为直角顶点,点P为直角顶点去分析求得答案.
类型二:构造相似来解决直角三角形存在性问题
例2.如图①,抛物线y=-x2+bx+8与x轴交于点A(-6,0),点B(点A在点B左侧),与y轴交于点C,点P为线段AO上的一个动点,过点P作x轴的垂线l与抛物线交于点E,连接AE,EC.
(1)求抛物线的解析式及点C的坐标;
(2)如图②,当EC∥x轴时,点P停止运动,此时,在抛物线上是否存在点G,使△AEG是以AE为直角边的直角三角形?若存在,请求出点G的坐标;若不存在,说明理由.
【分析】(1)用待定系数法求出抛物线解析式,令x=0时,求出y轴交点坐标;
(2)先求出点P的坐标,再分两种情况计算:当∠AEG=90°时,判断出△EMG∽△APE,得出比例式求解即可;当∠EAG=90°时,判断出△GNA∽△APE,得到比例式计算.
(
专题过关
)
1.
如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值;
(3)点D为抛物线对称轴上一点,当△BCD是以BC为直角边的直角三角形时,求点D的坐标.
2.如图,抛物线y=x2+bx+c与x轴交于A(3,0),B(-1,0)两点,过点B作直线BC⊥x轴,交直线y=-2x于点C.
(1)求该抛物线的解析式;
(2)求该抛物线的顶点D的坐标,并判断顶点D是否在直线y=-2x上;
(3)点P是抛物线上一动点,是否存在这样的点P(点A除外),使△PBC是以BC为直角边的直角三角形?若存在,求出所有满足条件的点P的坐标;若不存在,请说明理由.
3.如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,直接写出符合条件的点P的坐标;若不存在,请说明理由;
4.如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B的坐标为(1,0),抛物线y=-x2+bx+c经过A,B两点.
(1)求抛物线的解析式;
(2)点P是直线AB上方抛物线上的一点.过点P作PD垂直x轴于点D,交线段AB于点E,使PE=DE.
①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.
5.已知抛物线y=ax2+bx+c的顶点坐标为P(2,4).
(1)试写出b,c之间的关系式;
(2)当a>0时,若一次函数y=x+4的图象与y轴及该抛物线的交点依次为D,E,F,且E,F的横坐标x1与x2之间满足关系x2=6x1.
①求△ODE与△OEF的面积比;
②是否存在a,使得∠EPF=90°?若存在,求出a的值;若不存在,请说明理由.
6.已知开口向下的抛物线y=ax2﹣2ax+3与x轴的交点为A,B两点(点A在点B的左边),与y轴的交点为C,OC=3OA.
(1)请直接写出该抛物线解析式;
(2)如图,D为抛物线的顶点,连接BD,BC,P为对称轴右侧抛物线上一点.若∠ABD=∠BCP,求点P的坐标
(3)在(2)的条件下,M,N是抛物线上的动点.若∠MPN=90°,直线MN必过一定点,请求出该定点的坐标.
答案
例1.
(1)由题意得,解得
∴抛物线的解析式为y=-x2-2x+3.
∵对称轴为直线x=-1,抛物线经过A(1,0),∴B(-3,0).
设直线BC的解析式y=mx+n,把B(-3,0),C(0,3)分别代入y=mx+n,得解得∴直线BC的解析式为y=x+3.∴M(-1,2);
(2)设P(-1,t),∵B(-3,0),C(0,3),∴BC2=18,
PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10.
①若B为直角顶点,则BC2+PB2=PC2,即18+4+t2=t2-6t+10,解得t=-2;
②若C为直角顶点,则BC2+PC2=PB2,即18+t2-6t+10=4+t2,解得t=4;
③若P为直角顶点,则PB2+PC2=BC2,即4+t2+t2-6t+10=18,解得t1=,t2=.
综上所述,满足条件的点P共有四个,分别为:P1(-1,-2),P2(-1,4),P3(-1,),P4(-1,).
例2(1)∵点A(-6,0)在抛物线y=-x2+bx+8上,
∴0=-×(-6)2+(-6b)+8,解得b=-.
∴抛物线的解析式为y=-x2-x+8,令x=0,得y=8,∴C(0,8);
(2))存在.如图①,连接EG,AG,过点G作GM⊥l,GN⊥x轴,垂足分别为M,N,
图①
∵EC∥x轴,∴EP=CO=8.把y=8代入y=-x2-x+8,则8=-x2-x+8,解得x=0(舍去)或x=-2.∴P(-2,0)
.∴AP=AO-PO=4.
(ⅰ)如图①,当∠AEG=90°时,∵∠MEG+∠AEP=90°,∠AEP+∠EAP=90°,
∴∠MEG=∠EAP.又∵∠APE=∠EMG=90°,
∴△EMG∽△APE.∴=.设点G(m,-m2-m+8)(m>0),
则GN=MP=-m2-m+8.∴EM=EP-MP=8-(-m2-m+8)=m2+m,
MG=PN=PO+ON=2+m.
∴==,∴m=-2(舍去)或m=.∴G(,);
(ⅱ)如图②,当∠EAG=90°时,
图②
∵∠NAG+∠EAP=90°,∠AEP+∠EAP=90°,
∴∠NAG=∠AEP.∵∠APE=∠GNA=90°,∴△GNA∽△APE.∴=.
设点G(n,-
n2-n+8)(n>4),∴GN=n2+n-8,AN=AO+ON=6+n.
∴=.∴n=-6(舍去)或n=.∴G(,-)
.
综上,符合条件的G点的坐标为(,)或(,-).
(
专题过关
)
1.(1)由题意得,解得∴抛物线的解析式为y=x2-4x+3;
(2)如图①,过点P作PG∥CF交CB与点G.
图①
由题可知,直线BC的解析式为y=-x+3,OC=OB=3,∴∠OCB=45°.同理可知∠OFE=45°.∴△CEF为等腰直角三角形.∵PG∥CF,∴△GPE为等腰直角三角形.
∵F(0,m),C(0,3),∴CF=3-m.∵△CEF∽△GEP,∴EF=CF=
(3-m),
PE=PG.
设P(t,t2-4t+3)(1
(-t+3-t-m)=
(-m-2t+3)
.
∵点P是直线y=x+m与抛物线的交点,∴t2-4t+3=t+m.
∴PE+EF=
(3-m)+
(-m-2t+3)=
(-2t-2m+6)=-
(t+m-3)=-
(t2-4t)=
-
(t-2)2+4.
∴当t=2时,PE+EF最大,最大值为4;
(3)由(1)知对称轴x=2,设点D(2,n),如图②.
图②
当△BCD是以BC为直角边的直角三角形时,分两种情况讨论:
(ⅰ)D在C上方D1位置时,由勾股定理得CD12+BC2=BD12,即(2-0)2+(n-3)2+(3)2=(3-2)2+(0-n)2
,解得n=5;
(ⅱ)D在C下方D2位置时,由勾股定理得BD22+BC2=CD22
即(2-3)2+(n-0)2+(3)2=(2-0)2+(n-3)2
,解得n=-1,
综上所述,当△BCD是以BC为直角边的直角三角形时,D为(2,5)或(2,-1).
2.:(1)∵y=x2+bx+c与x轴交于A(3,0),B(-1,0)两点,
∴解得,∴抛物线的解析式为y=x2-x-1;
(2)由y=x2-x-1=(x-1)2-,∴抛物线的顶点D的坐标为(1,-).
把x=1代入y=-2x中得y=-2.
∵-≠-2,∴顶点D不在直线y=-2x上;
(3)存在.理由如下:如图,过点C作x轴的平行线,与该抛物线交于点P1,P2,连接BP1,BP2.
∵直线BC⊥x轴,∴△P1BC、△P2BC都是直角三角形.
把x=-1代入y=-2x中得y=-2×(-1)=2.∴C(-1,2).
∴把y=2代入y=x2-x-1中,得x2-x-1=2,
解得x1=+1,x2=-+1.∴P1(+1,2),P2(-+1,2).
3.
(1)设抛物线解析式为y=a(x+1)(x-3),即y=ax2-2ax-3a.
∴-2a=2,解得a=-1,∴抛物线解析式为y=-x2+2x+3.
当x=0时,y=-x2+2x+3=3,则C(0,3).
设直线AC的解析式为y=px+q,
把A(-1,0),C(0,3)代入得解得∴直线AC的解析式为y=3x+3.
(2)∵y=-x2+2x+3=-(x-1)2+4,∴顶点D的坐标为(1,4).
如图,作B点关于y轴的对称点B′,则B′(-3,0),连接DB′交y轴于M.
∵MB=MB′,∴MB+MD=MB′+MD=DB′,此时MB+MD的值最小.
∵BD的值不变,∴此时△BDM的周长最小.易得直线DB′的解析式为y=x+3.
当x=0时,y=x+3=3,∴点M的坐标为(0,3).
(3)存在,符合条件的点P的坐标为(,)或(,-).
4.(1)在Rt△ABC中,由点B的坐标可知OB=1.
∵OC=2OB,∴OC=2,则BC=3.又∵tan∠ABC=2,
∴AC=2BC=6,则点A的坐标为(-2,6).
把点A,B的坐标代入抛物线y=-x2+bx+c中,得
解得∴该抛物线的解析式为y=-x2-3x+4.
(2)①由点A(-2,6)和点B(1,0)的坐标易得直线AB的解析式为y=-2x+2.
如图,设点P的坐标为(m,-m2-3m+4),则点E的坐标为(m,-2m+2),点D的坐标为(m,0)
.则PE=-m2-m+2,DE=-2m+2,
由PE=DE得-m2-m+2=(-2m+2),解得m=±1.
又∵-2<m<1,∴m=-1,∴点P的坐标为(-1,6).
②∵M在直线PD上,且P(-1,6),设M(-1,y),
∴AM2=(-1+2)2+(y-6)2=1+(y-6)2,BM2=(1+1)2+y2=4+y2,AB2=(1+2)2+62=45.
分三种情况:
(ⅰ)当∠AMB=90°时,有AM2+BM2=AB2,∴1+(y-6)2+4+y2=45,解得y=3±.
∴M(-1,3+)或(-1,3-);
(ⅱ)当∠ABM=90°时,有AB2+BM2=AM2,∴45+4+y2=1+(y-6)2,解得y=-1,∴M(-1,-1).
(ⅲ)当∠BAM=90°时,有AM2+AB2=BM2,
∴1+(y-6)2+45=4+y2,解得y=,∴M(-1,).
综上所述,点M的坐标为(-1,3+)或(-1,3-)或(-1,-1)或(-1,).
5.(1)∵抛物线顶点坐标为(2,4),
∴抛物线解析式为y=a(x﹣2)2+4=ax2﹣4ax+4a+4,
∴b=﹣4a,c=4a+4.∴b+c=4;
(2)①由题意可知△ODE和△ODF的底边DE、DF边上的高相同,
∴S△ODE:S△ODF=DE:DF=x1:x2=1:6.∴S△ODE:S△OEF=1:5;
②如图,分别过E,F作x轴的垂线,垂足分别为G、H,交直线DP于点M、N,
∵直线y=x+4,∴设点E坐标为(m,m+4),则点F的坐标为(6m,6m+4).
∴EM=EG﹣MG=m+4﹣4=m,FN=FH﹣NH=6m+4﹣4=6m,PM=PD﹣MD=2﹣m,PN=DN﹣PD=6m﹣2,
∵∠EPF=90°,∴∠EPM+∠FPN=90°,且∠FPN+∠PFN=90°.∴∠EPM=∠PFN.
∴△EPM∽△PEN.∴,即.整理可得6m2+7m+2=0,解得m=或m=,
当m=时,点E(,),F(3,7),把F点坐标代入抛物线解析式可得a+4=7,解得a=3,
∴抛物线解析式为y=3(x﹣2)2+4,当x=时,代入可求得y=≠,即点E不在该抛物线图象上,不符合题意.
当m=时,点E(,),F(4,8),把F点坐标代入抛物线解析式可求得a=1.
∴抛物线解析式为y=(x﹣2)2+4.
当x=时,代入可求得y=≠,即点E不在抛物线图象上,不符合题意,
综上可知不存在满足条件的a的值.
6.(1)当x=0时,y=ax2﹣2ax+3=3,
∴C(0,3),OC=3OA=3.∴OA=1,A(﹣1,0).
把点A(﹣1,0)代入抛物线解析式,得:a+2a+3=0,解得a=﹣1.
∴抛物线解析式为y=﹣x2+2x+3;
(2)如图1,若点P在抛物线对称轴右侧且在x轴上方,
过点P作PE∥y轴交BC于点E,PF⊥BC于点F,过点D作DH⊥x轴于点H,
∴∠CFP=∠BHD=90°.
∵当y=﹣x2+2x+3=0时,解得:x1=﹣1,x2=3.∴A(﹣1,0),B(3,0).
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点D(1,4).∴DH=4,BH=3﹣1=2.
∴BD=.
∴Rt△BDH中,sin∠ABD=.
∵C(0,3)∴BC=,PC=.
设直线BC解析式为y=kx+b,∴解得:,
∴直线BC解析式为y=﹣x+3.
设P(p,﹣p2+2p+3)(1<p<3),则E(p,﹣p+3),
∴PE=﹣p2+2p+3﹣(﹣p+3)=﹣p2+3p.
∵S△BCP=PE?OB=BC?PF,∴PF=.
∵∠ABD=∠BCP,∴Rt△CPF中,sin∠BCP==sin∠ABD=.
∴PF=PC.∴PF2=PC2.解得p1=﹣1(舍去),p2=.
∴﹣p2+2p+3=.∴点P坐标为(,).
如图2,若点P在x轴下方,
∵tan∠ABD==2>tan45°,∴∠ABD>45°.
∵∠BCP<∠BOC即∠BCP<45°,∴∠ABD与∠BCP不可能相等.
综上所述,点P坐标为(,);
(3)如图3,过P作PH∥y轴,分别过点M、N作MG⊥PH于G,NH⊥PH于H.
设直线MN的解析式为y=kx+n,M(x1,y1)、N(x2,y3),
令kx+n=﹣x2+2x+3,即=x2+(k﹣2)x+n﹣3=0,
∴x1+x2=2﹣k,x1x2=n﹣3.
∴y1+y2=k(x1+x2)+2n=k(2﹣k)+2n.
y1y2=(kx1+n)(kx2+n)=k2x1x2+nk(x1+x2)+n2=﹣3k2+2nk+n2,
∵∠G=∠MPN=∠H,∴△MPG∽△PNH.∴
.
∵P坐标为(,),MG=﹣x1,PH=y1﹣,HN=,GP=.
∴.整理,得.
∴.
解得
k1=﹣3n+,k2=.
∴直线MN;y=(﹣3n+)x+n=(﹣3x+1)n+,过定点(,);
或y=()x+n=()n+,过定点(,)即P点,舍去.
∴直线MN过定点(,).
16
/
16
同课章节目录
