人教版初中数学八年级下册19.1.1函数课件(共17张PPT)
文档属性
| 名称 | 人教版初中数学八年级下册19.1.1函数课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-02 17:46:37 | ||
图片预览





文档简介
(共17张PPT)
19.1.1
函数
第十九章一次函数
1.体会运动变化过程中的数量变化.
2.从典型实例中抽象概括出函数的概念,了解函数的概念.
教学重点:
在了解变量之间的对应关系的基础上,抽象出函数的概念.
教学难点:
概括并理解函数概念中的单值对应关系.
S
=
60
t
y=10x
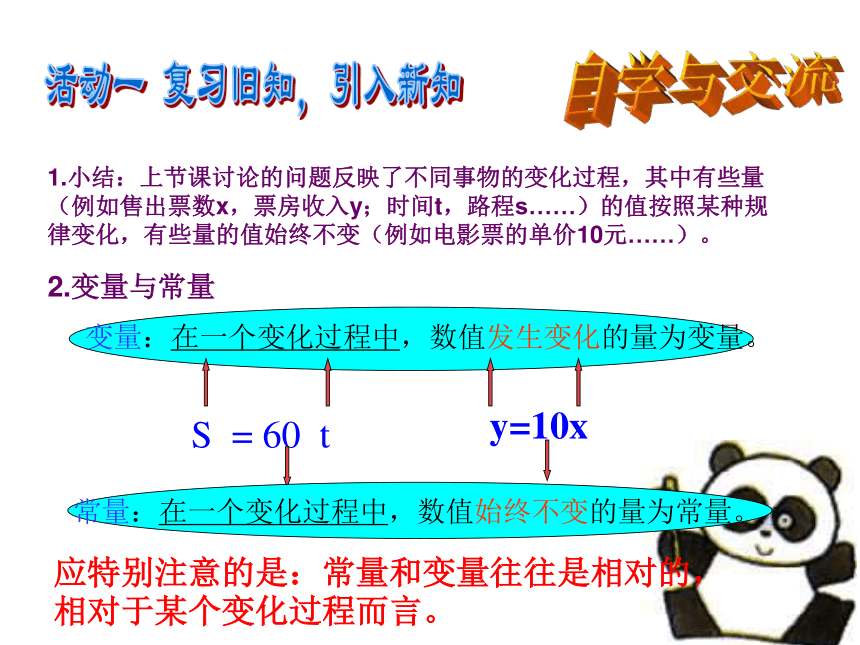
1.小结:上节课讨论的问题反映了不同事物的变化过程,其中有些量(例如售出票数x,票房收入y;时间t,路程s……)的值按照某种规律变化,有些量的值始终不变(例如电影票的单价10元……)。
常量:在一个变化过程中,数值始终不变的量为常量。
变量:在一个变化过程中,数值发生变化的量为变量。
2.变量与常量
应特别注意的是:常量和变量往往是相对的,相对于某个变化过程而言。
上述几个问题有共同之处吗?
请同学们分组交流。
随着确定一个值
1、每个变化的过程中都存在着
个变量;
2、当其中的一个变量变化时,另一个变量也在
;
3、当一个变量确定一个值时,另一个变量也
.
两
随着变化
S
=
60
t
y=10x
函数的定义:
1
在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量
,y是x的函数。
2
如果当x=a时y=b,那么b叫做当自变量x的值为a时y的函数值。
函数关系的三种表示方法:
解析法、列表法、图象法
综合以上这些现象,你能再次归纳出上面所有事例的变量之间关系的共同特点吗?
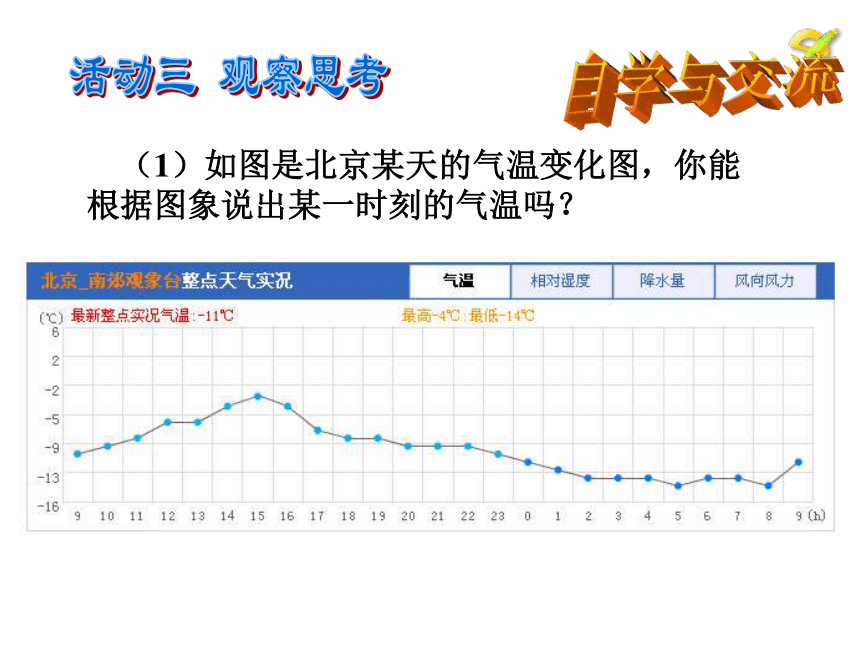
(1)如图是北京某天的气温变化图,你能根据图象说出某一时刻的气温吗?
(2)在下面的我国人口数统计表中,年份与人口数
可以记作两个变量x与y,对于表中每一个确定的年
份(x),都对应着一个确定的人口数(y)吗?
年份
x
人口数y/亿
1984
10.34
1989
11.06
1994
11.76
1999
12.52
2010
13.71
对于x的每一个值,y总有唯一的值与它对应,y才是x的函数。
2.下列曲线中,表示y不是x的函数是( )
B
3.一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km。
(1)写出表示y与x的函数关系的式子。
(2)指出自变量x的取值范围。
(3)汽车行驶200
km时,油箱中还有多少油?
解:(1)
函数关系式为
y
=
50-0.1x。
(2)
由x≥0及50-0.1x
≥0,得0
≤
x
≤
500。
所以自变量的取值范围是
0
≤
x
≤
500。
(3)当
x
=
200时,函数
y
的值为y=50-0.1×200=30。
因此,当汽车行驶200
km时,油箱中还有油30L。
归纳:像y=50-0.1x这样,描述自变量和函数之间的关系式叫函数关系式,也叫做函数解析式。
(1)你认为函数与自变量之间有哪些联系?
(2)
理解函数解析式.
课堂小结
课本习题第4、5、10、11题
练习1.写出下列问题中的函数解析式,并指出其中的自变量和函数.
(1)用20cm的铁丝所围的长方形的长x(cm)与面积S(cm2)的关系.
(2)一盛满30吨水的水箱,每小时流出0.5吨水,试用流水时间t(小时)表示水箱中的剩水量y(吨).
解:(1)S=10x-x?,
S是x的函数,x是自变量.
(2)y=30-0.5t,
y是t的函数,t是自变量.
练习2.当x=2和x=-3时,分别求下列函数的函数值.
(1)y=(x+1)(x-2)
(2)y=2x?-3x+2
练习3.已知函数y=x?-x+2,当x=2时,函数值y=______;
已知函数y=3x?,当x=_______时,函数值y=12.
4
±2
解:(1)当x=2时,y=(x+1)(x-2)=(2+1)×(2-2)=0;
当x=-3时,y=(x+1)(x-2)=(-3+1)×(-3-2)=10.
(2)当x=2时,y=2x?-3x+2=2×2?-3×2+2=4;
当x=-3时,y=2x?-3x+2=2×(-3)?-3×(-3)+2=29.
练习4.我市白天乘坐出租车收费标准如下:乘坐里程不超过3公里,一律收费8元;超过3公里时,超过3公里的部分,每公里加收1.8元;设乘坐出租车的里程为x(公里)(x为整数),相对应的收费为y(元).
(1)请分别写出当0<x≤3和x>3时,表示y与x的关系式,并直接写出当x=2和x=6时对应的y值;
(2)当0<x≤3和x>3时,y都是x的函数吗?为什么?
解:(1)当0<x≤3时,y=8;
当x>3时,y=8+1.8(x-3)=1.8x+2.6.
当x=2时,y=8;x=6时,y=1.8×6+2.6=13.4.
(2)当0<x≤3和x>3时,y都是x的函数,因为对于x的每一个确定的值,y都有唯一确定的值与其对应.
再见!
19.1.1
函数
第十九章一次函数
1.体会运动变化过程中的数量变化.
2.从典型实例中抽象概括出函数的概念,了解函数的概念.
教学重点:
在了解变量之间的对应关系的基础上,抽象出函数的概念.
教学难点:
概括并理解函数概念中的单值对应关系.
S
=
60
t
y=10x
1.小结:上节课讨论的问题反映了不同事物的变化过程,其中有些量(例如售出票数x,票房收入y;时间t,路程s……)的值按照某种规律变化,有些量的值始终不变(例如电影票的单价10元……)。
常量:在一个变化过程中,数值始终不变的量为常量。
变量:在一个变化过程中,数值发生变化的量为变量。
2.变量与常量
应特别注意的是:常量和变量往往是相对的,相对于某个变化过程而言。
上述几个问题有共同之处吗?
请同学们分组交流。
随着确定一个值
1、每个变化的过程中都存在着
个变量;
2、当其中的一个变量变化时,另一个变量也在
;
3、当一个变量确定一个值时,另一个变量也
.
两
随着变化
S
=
60
t
y=10x
函数的定义:
1
在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量
,y是x的函数。
2
如果当x=a时y=b,那么b叫做当自变量x的值为a时y的函数值。
函数关系的三种表示方法:
解析法、列表法、图象法
综合以上这些现象,你能再次归纳出上面所有事例的变量之间关系的共同特点吗?
(1)如图是北京某天的气温变化图,你能根据图象说出某一时刻的气温吗?
(2)在下面的我国人口数统计表中,年份与人口数
可以记作两个变量x与y,对于表中每一个确定的年
份(x),都对应着一个确定的人口数(y)吗?
年份
x
人口数y/亿
1984
10.34
1989
11.06
1994
11.76
1999
12.52
2010
13.71
对于x的每一个值,y总有唯一的值与它对应,y才是x的函数。
2.下列曲线中,表示y不是x的函数是( )
B
3.一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km。
(1)写出表示y与x的函数关系的式子。
(2)指出自变量x的取值范围。
(3)汽车行驶200
km时,油箱中还有多少油?
解:(1)
函数关系式为
y
=
50-0.1x。
(2)
由x≥0及50-0.1x
≥0,得0
≤
x
≤
500。
所以自变量的取值范围是
0
≤
x
≤
500。
(3)当
x
=
200时,函数
y
的值为y=50-0.1×200=30。
因此,当汽车行驶200
km时,油箱中还有油30L。
归纳:像y=50-0.1x这样,描述自变量和函数之间的关系式叫函数关系式,也叫做函数解析式。
(1)你认为函数与自变量之间有哪些联系?
(2)
理解函数解析式.
课堂小结
课本习题第4、5、10、11题
练习1.写出下列问题中的函数解析式,并指出其中的自变量和函数.
(1)用20cm的铁丝所围的长方形的长x(cm)与面积S(cm2)的关系.
(2)一盛满30吨水的水箱,每小时流出0.5吨水,试用流水时间t(小时)表示水箱中的剩水量y(吨).
解:(1)S=10x-x?,
S是x的函数,x是自变量.
(2)y=30-0.5t,
y是t的函数,t是自变量.
练习2.当x=2和x=-3时,分别求下列函数的函数值.
(1)y=(x+1)(x-2)
(2)y=2x?-3x+2
练习3.已知函数y=x?-x+2,当x=2时,函数值y=______;
已知函数y=3x?,当x=_______时,函数值y=12.
4
±2
解:(1)当x=2时,y=(x+1)(x-2)=(2+1)×(2-2)=0;
当x=-3时,y=(x+1)(x-2)=(-3+1)×(-3-2)=10.
(2)当x=2时,y=2x?-3x+2=2×2?-3×2+2=4;
当x=-3时,y=2x?-3x+2=2×(-3)?-3×(-3)+2=29.
练习4.我市白天乘坐出租车收费标准如下:乘坐里程不超过3公里,一律收费8元;超过3公里时,超过3公里的部分,每公里加收1.8元;设乘坐出租车的里程为x(公里)(x为整数),相对应的收费为y(元).
(1)请分别写出当0<x≤3和x>3时,表示y与x的关系式,并直接写出当x=2和x=6时对应的y值;
(2)当0<x≤3和x>3时,y都是x的函数吗?为什么?
解:(1)当0<x≤3时,y=8;
当x>3时,y=8+1.8(x-3)=1.8x+2.6.
当x=2时,y=8;x=6时,y=1.8×6+2.6=13.4.
(2)当0<x≤3和x>3时,y都是x的函数,因为对于x的每一个确定的值,y都有唯一确定的值与其对应.
再见!
