人教版初中数学八年级下册19.2一次函数同步测试题含答案
文档属性
| 名称 | 人教版初中数学八年级下册19.2一次函数同步测试题含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 142.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 17:25:49 | ||
图片预览


文档简介
人教版初中数学八年级下册第19章2节一次函数同步测试题
一、选择题
1.下列说法中不正确的是( )
A.一次函数不一定是正比例函数
B.不是一次函数就一定不是正比例函数
C.正比例函数是特殊的一次函数
D.不是正比例函数就一定不是一次函数
2.若y=x+2-3b是正比例函数,则b的值是( )
A.0
B.-
C.
D.-
3.下列函数:①y=x;②y=;③y=;④y=2x+1,其中一次函数的个数是( )
A.1
B.2
C.3
D.4
4.函数y=(m-2)xn-1+n是一次函数,m,n应满足的条件是( )
A.m≠2且n=0
B.m=2且n=2
C.m≠2且n=2
D.m=2且n=0
5.正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=x+k的图象大致是( )
A.
B.
C.
D.
6.一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是( )
A.x>0
B.x<0
C.x>2
D.x<2
7.关于x的一次函数y=kx+k2+1的图象可能正确的是( )
A.
B.
C.
D.
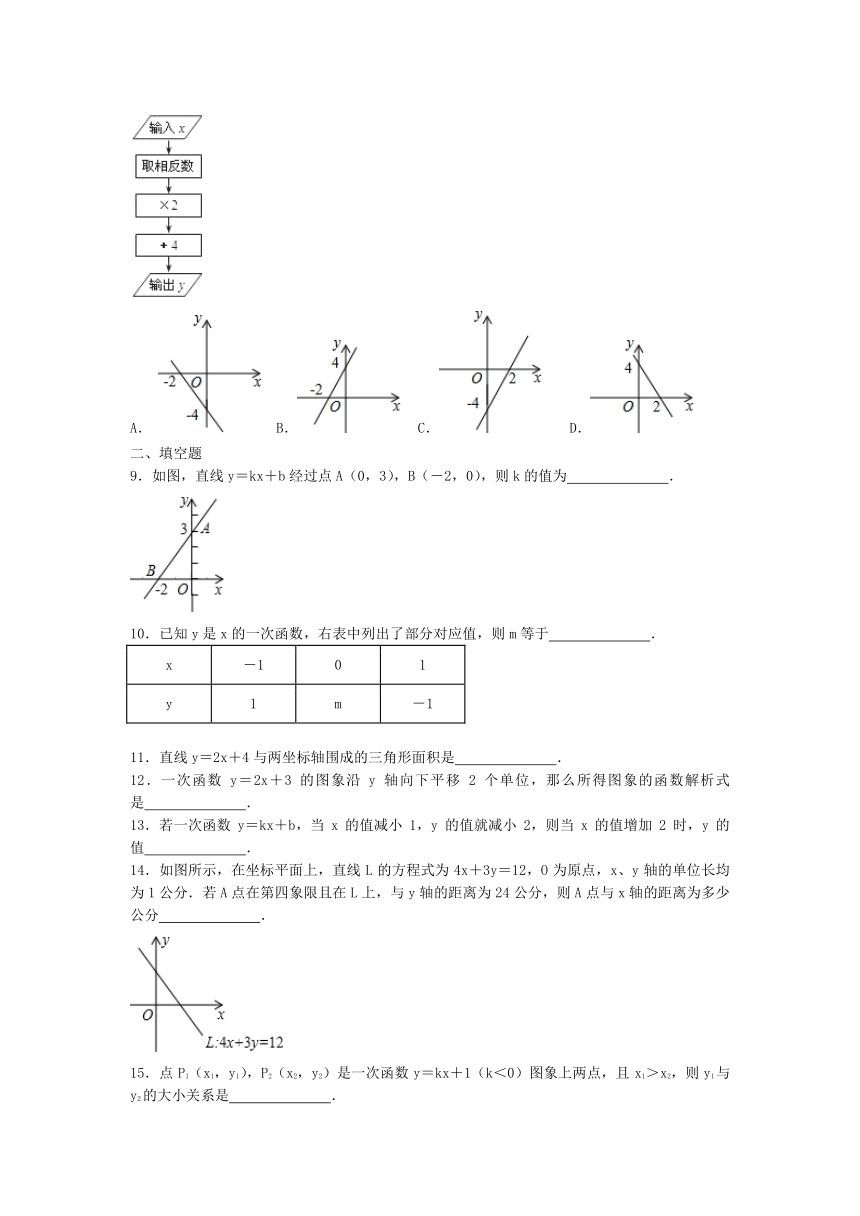
8.如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
A.
B.
C.
D.
二、填空题
9.如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为
.
10.已知y是x的一次函数,右表中列出了部分对应值,则m等于
.
x
-1
0
1
y
1
m
-1
11.直线y=2x+4与两坐标轴围成的三角形面积是
.
12.一次函数y=2x+3的图象沿y轴向下平移2个单位,那么所得图象的函数解析式是
.
13.若一次函数y=kx+b,当x的值减小1,y的值就减小2,则当x的值增加2时,y的值
.
14.如图所示,在坐标平面上,直线L的方程式为4x+3y=12,O为原点,x、y轴的单位长均为1公分.若A点在第四象限且在L上,与y轴的距离为24公分,则A点与x轴的距离为多少公分
.
15.点P1(x1,y1),P2(x2,y2)是一次函数y=kx+1(k<0)图象上两点,且x1>x2,则y1与y2的大小关系是
.
16.给出四条直线:y=kx-3、y=-1、y=3和x=1,已知它们围成的四边形的面积为12,求k的值
.
三、解答题
17.作出函数y=x-3的图象并回答:(1)当x的值增加时,y的值如何变化?(2)当x取何值时,y>0,y=0,y<0.
18.小明根据某个一次函数关系式填写了下面的这张表:其中有一格不慎被墨迹遮住了,想想看,该空格里原来填的数是多少?写出你的理由.
?x
-2
?墨水遮盖
?0
?1
?y
?3
-1
?1
?0
19.已知一次函数y=x+6-m,求:
(1)m为何值时,函数图象交y轴于正半轴?
(2)m为何值时,函数图象与y轴的交点在x轴的下方?
(3)m为何值时,图象经过原点?
20.某个一次函数y=kx+b的图象位置大致如图所示,试分别确定k、b的符号,并说出函数的性质.
21.如图所示,已知直线y=kx-2经过M点,求此直线与x轴交点坐标和直线与两坐标轴围成三角形的面积.
22.某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在第10天、第30天的需水量分别为2000千克、3000千克,在第40天后每天的需水量比前一天增加100千克.
(1)分别求出x≤40和x≥40时y与x之间的关系式;
(2)如果这些农作物每天的需水量大于或等于4000千克时需要进行人工灌溉,那么应从第几天开始进行人工灌溉?
24.已知一个一次函数的自变量的取值范围是2≤x≤6,函数值的取值范围是5≤y≤9,求这个一次函数解析式.
答案
1.
B
2.
C
3.
C
4.
C
5.
A
6.
C
7.
C
8.
D
9.
10.
0
11.
解:当x=0时,y=4;当y=0时,x=-2;所以直线y=2x+4与两坐标轴围成的三角形面积是×4×|-2|=4.
12.
y=2x+1
13.
增加4
14.
解:根据题意可设A点坐标为(24,b),b<0,
因为点A在直线4x+3y=12上,
故把A点代入得:4×24+3b=12,解得b=-28.
故A点与x轴的距离为|-28|=28.
15.
y1<y2
16.
解:如图所示,根据题意,得
A(1,3),B(1,-1),C(,-1),D(,3).
显然ABCD是梯形,且梯形的高是4,根据梯形的面积是12,则梯形的上下底的和是6,则有
①当k<0时,1-+1-=6,
∴2-=6,
∴=-4,
解得k=-2;
②当k>0时,-1+-1=6,
∴=8,
解得k=1.
综上所述,则k=-2或1.
17.
解:
当x=0时,y=-3,
当y=0时,x-3=0,
解得x=6,
∴函数图象与两坐标轴的交点为(0,-3)(6,0).
(1)由图可知,y的值随着x的增大而增大;
(2)x>6时,y>0;
x=6时,y=0;
x<6时,y<0.
18.
解:设y=kx+b,根据图中的信息得
求得:k=-1,b=1,
∴y=-x+1
当y=-1时,-1=-x+1,x=2,
所以空格里原来填的数是2.
19.
解:(1)由题意得,6-m>0,解得,m<6;
(2)由题意得,6-m<0,解得,m>6;
(3)由题意得,6-m=0,解得,m=6.
20.
解:图(1)中,∵直线y=kx+b的图象在一、二、四象限,
∴k<0,b>0;
∴y随x的增大而减小,函数从左到右逐渐下降;直线与y轴交于正半轴.
图(2)中,∵直线y=kx+b的图象在一、二、三象限,
∴k>0,b>0;
∴y随x的增大而增大,函数从左到右逐渐上升;直线与y轴交于正半轴.
21.
解:由图象可知,点M(-2,4)在直线y=kx-2上,
∴-2k-2=4,
解得:k=-3,
∴直线的解析式为y=-3x-2,
令y=0,可得x=-,
∴直线与x轴的交点坐标为:(-,0),
令x=0,可得y=-2,
∴直线与y轴的交点坐标为(0,-2),
∴直线与两坐标轴围成的三角线的面积=××|-2|=.
22.
解:(1)当x≤40时,设y=kx+b.
根据题意,得
解这个方程组,得
∴当x<40时,y与x之间的关系式是y=50x+1500;
∴当x=40时,y=50×40+1500=3500;
当x≥40时,根据题意,得y=100(x-40)+3500,即y=100x-500.
∴当x≥40时,y与x之间的关系式是y=100x-500.
(2)当y≥4000时,y与x之间的关系式是y=100x-500.
解不等式100x-500≥4000.
得x≥45.
∴应从第45天开始进行人工灌溉.
22.
解:设该一次函数的关系式是:y=kx+b(k≠0).
一次函数y=kx+b的自变量的取值范围是:2≤x≤6,相应函数值的取值范围是:5≤y≤9,则
①当k>0函数为递增函数,即x=2,y=5时,
x=6时,y=9.
根据题意列出方程组:
,
解得:,
则这个函数的解析式是:y=x+3;
②当k<0函数为递减函数时,
则,
解得,
所以该一次函数的解析式为y=-x+11,
综上所述,该一次函数的解析式是y=x+3,或y=-x+11.
一、选择题
1.下列说法中不正确的是( )
A.一次函数不一定是正比例函数
B.不是一次函数就一定不是正比例函数
C.正比例函数是特殊的一次函数
D.不是正比例函数就一定不是一次函数
2.若y=x+2-3b是正比例函数,则b的值是( )
A.0
B.-
C.
D.-
3.下列函数:①y=x;②y=;③y=;④y=2x+1,其中一次函数的个数是( )
A.1
B.2
C.3
D.4
4.函数y=(m-2)xn-1+n是一次函数,m,n应满足的条件是( )
A.m≠2且n=0
B.m=2且n=2
C.m≠2且n=2
D.m=2且n=0
5.正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=x+k的图象大致是( )
A.
B.
C.
D.
6.一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是( )
A.x>0
B.x<0
C.x>2
D.x<2
7.关于x的一次函数y=kx+k2+1的图象可能正确的是( )
A.
B.
C.
D.
8.如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
A.
B.
C.
D.
二、填空题
9.如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为
.
10.已知y是x的一次函数,右表中列出了部分对应值,则m等于
.
x
-1
0
1
y
1
m
-1
11.直线y=2x+4与两坐标轴围成的三角形面积是
.
12.一次函数y=2x+3的图象沿y轴向下平移2个单位,那么所得图象的函数解析式是
.
13.若一次函数y=kx+b,当x的值减小1,y的值就减小2,则当x的值增加2时,y的值
.
14.如图所示,在坐标平面上,直线L的方程式为4x+3y=12,O为原点,x、y轴的单位长均为1公分.若A点在第四象限且在L上,与y轴的距离为24公分,则A点与x轴的距离为多少公分
.
15.点P1(x1,y1),P2(x2,y2)是一次函数y=kx+1(k<0)图象上两点,且x1>x2,则y1与y2的大小关系是
.
16.给出四条直线:y=kx-3、y=-1、y=3和x=1,已知它们围成的四边形的面积为12,求k的值
.
三、解答题
17.作出函数y=x-3的图象并回答:(1)当x的值增加时,y的值如何变化?(2)当x取何值时,y>0,y=0,y<0.
18.小明根据某个一次函数关系式填写了下面的这张表:其中有一格不慎被墨迹遮住了,想想看,该空格里原来填的数是多少?写出你的理由.
?x
-2
?墨水遮盖
?0
?1
?y
?3
-1
?1
?0
19.已知一次函数y=x+6-m,求:
(1)m为何值时,函数图象交y轴于正半轴?
(2)m为何值时,函数图象与y轴的交点在x轴的下方?
(3)m为何值时,图象经过原点?
20.某个一次函数y=kx+b的图象位置大致如图所示,试分别确定k、b的符号,并说出函数的性质.
21.如图所示,已知直线y=kx-2经过M点,求此直线与x轴交点坐标和直线与两坐标轴围成三角形的面积.
22.某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在第10天、第30天的需水量分别为2000千克、3000千克,在第40天后每天的需水量比前一天增加100千克.
(1)分别求出x≤40和x≥40时y与x之间的关系式;
(2)如果这些农作物每天的需水量大于或等于4000千克时需要进行人工灌溉,那么应从第几天开始进行人工灌溉?
24.已知一个一次函数的自变量的取值范围是2≤x≤6,函数值的取值范围是5≤y≤9,求这个一次函数解析式.
答案
1.
B
2.
C
3.
C
4.
C
5.
A
6.
C
7.
C
8.
D
9.
10.
0
11.
解:当x=0时,y=4;当y=0时,x=-2;所以直线y=2x+4与两坐标轴围成的三角形面积是×4×|-2|=4.
12.
y=2x+1
13.
增加4
14.
解:根据题意可设A点坐标为(24,b),b<0,
因为点A在直线4x+3y=12上,
故把A点代入得:4×24+3b=12,解得b=-28.
故A点与x轴的距离为|-28|=28.
15.
y1<y2
16.
解:如图所示,根据题意,得
A(1,3),B(1,-1),C(,-1),D(,3).
显然ABCD是梯形,且梯形的高是4,根据梯形的面积是12,则梯形的上下底的和是6,则有
①当k<0时,1-+1-=6,
∴2-=6,
∴=-4,
解得k=-2;
②当k>0时,-1+-1=6,
∴=8,
解得k=1.
综上所述,则k=-2或1.
17.
解:
当x=0时,y=-3,
当y=0时,x-3=0,
解得x=6,
∴函数图象与两坐标轴的交点为(0,-3)(6,0).
(1)由图可知,y的值随着x的增大而增大;
(2)x>6时,y>0;
x=6时,y=0;
x<6时,y<0.
18.
解:设y=kx+b,根据图中的信息得
求得:k=-1,b=1,
∴y=-x+1
当y=-1时,-1=-x+1,x=2,
所以空格里原来填的数是2.
19.
解:(1)由题意得,6-m>0,解得,m<6;
(2)由题意得,6-m<0,解得,m>6;
(3)由题意得,6-m=0,解得,m=6.
20.
解:图(1)中,∵直线y=kx+b的图象在一、二、四象限,
∴k<0,b>0;
∴y随x的增大而减小,函数从左到右逐渐下降;直线与y轴交于正半轴.
图(2)中,∵直线y=kx+b的图象在一、二、三象限,
∴k>0,b>0;
∴y随x的增大而增大,函数从左到右逐渐上升;直线与y轴交于正半轴.
21.
解:由图象可知,点M(-2,4)在直线y=kx-2上,
∴-2k-2=4,
解得:k=-3,
∴直线的解析式为y=-3x-2,
令y=0,可得x=-,
∴直线与x轴的交点坐标为:(-,0),
令x=0,可得y=-2,
∴直线与y轴的交点坐标为(0,-2),
∴直线与两坐标轴围成的三角线的面积=××|-2|=.
22.
解:(1)当x≤40时,设y=kx+b.
根据题意,得
解这个方程组,得
∴当x<40时,y与x之间的关系式是y=50x+1500;
∴当x=40时,y=50×40+1500=3500;
当x≥40时,根据题意,得y=100(x-40)+3500,即y=100x-500.
∴当x≥40时,y与x之间的关系式是y=100x-500.
(2)当y≥4000时,y与x之间的关系式是y=100x-500.
解不等式100x-500≥4000.
得x≥45.
∴应从第45天开始进行人工灌溉.
22.
解:设该一次函数的关系式是:y=kx+b(k≠0).
一次函数y=kx+b的自变量的取值范围是:2≤x≤6,相应函数值的取值范围是:5≤y≤9,则
①当k>0函数为递增函数,即x=2,y=5时,
x=6时,y=9.
根据题意列出方程组:
,
解得:,
则这个函数的解析式是:y=x+3;
②当k<0函数为递减函数时,
则,
解得,
所以该一次函数的解析式为y=-x+11,
综上所述,该一次函数的解析式是y=x+3,或y=-x+11.
