人教版数学八年级下册19.2.3 一次函数与一元一次不等式教案
文档属性
| 名称 | 人教版数学八年级下册19.2.3 一次函数与一元一次不等式教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 138.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-02 00:00:00 | ||
图片预览


文档简介
19.2.3
一次函数与一元一次不等式
教学目标
知识与技能
理解一次函数与一元一次不等式之间的联系,会用函数观点得出一元一次不等式的解集
过程与方法
经历用函数图象表示不等式解集的过程,进一步体会数形结合思想.
情感态度与价值观
通过探究一次函数与一元一次不等式的联系,使学生感受数形结合思想的魅力,体会从不同角度认识事物本质的方法.
学情分析
八年级下的学生,具备了一定的推理能力和认知水平,掌握了基本的教学方法,但他们运用数学方法解决问题的能力不强,对知识的获取正处于从感性向理性转变的阶段.因此,在教学设计时,应遵循认知规律,由形象到抽象,由易到难,注重引导.
尽管学生已经掌握了方程、函数和不等式的相关知识,但这些知识是零散的,不能融会贯通,不能灵活运用知识选择最优方法来解决问题。第二,学生对数形结合方法的运用不够熟练,缺乏全面分析问题的能力。第三,不能准确的找到问题的本质特征。因此,找到一次函数与一元一次不等式之间的联系并准确的表述是本节课的难点。需要教师逐步引导.
教学重难点
重点:理解一次函数与一元一次不等式的联系
难点:把一次函数图象与一元一次不等式建立联系并能表述
突破难点:设计导学案让学生动手做一做,画一画,想一想,根据教师的引导发现并归纳结论.同时利用电子白板的写、画功能在电子白板上展示,直观形象进一步帮助学生理解.
四、教法与学法
教法:启发式教学,多媒体辅助
学法:独立思考,自主探究,合作交流
教学准备
多媒体课件
教学过程
课题引入
计算:
还有其他的方法吗?
如何利用函数图象来求解?
(设计意图)温故知新,在二元一次方程组的基础上引入新课,提出问题,引发学生思考.
(二
)
探究新知
探究一:
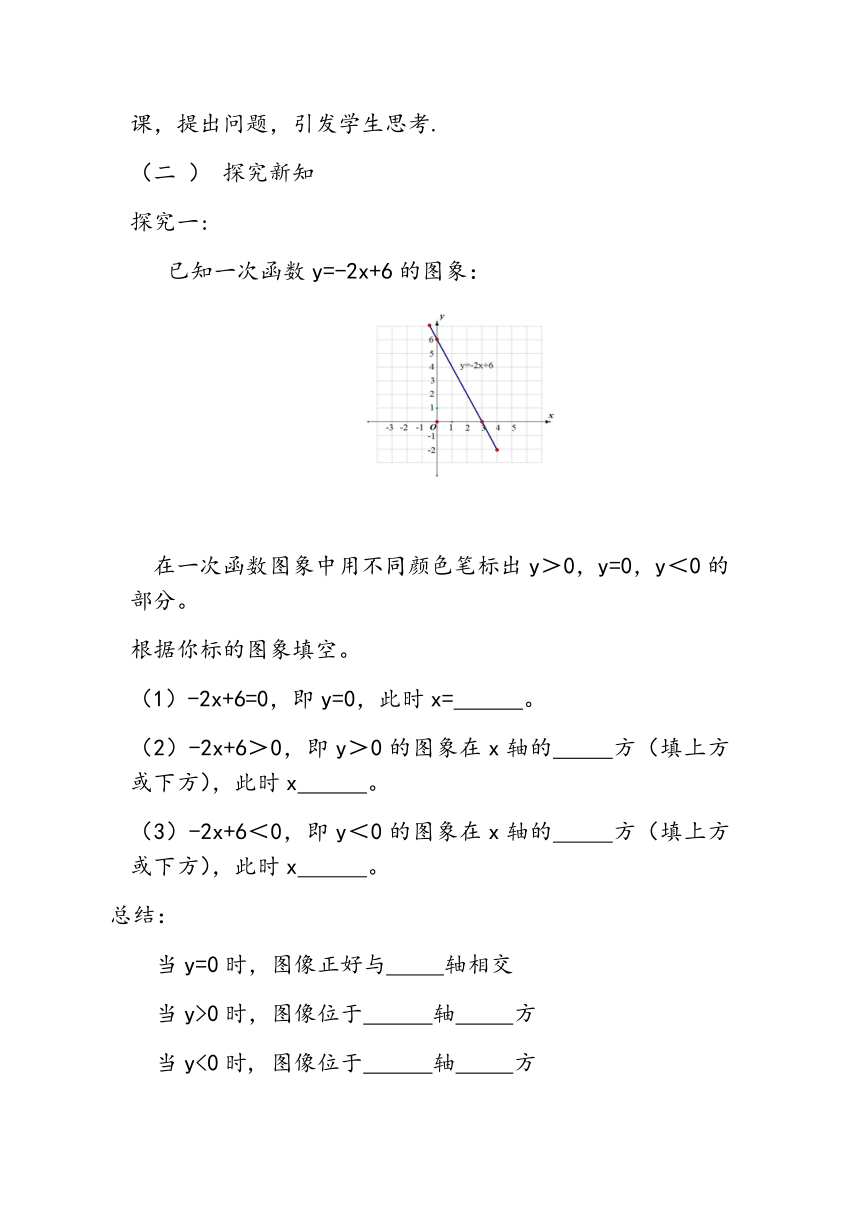
已知一次函数y=-2x+6的图象:
在一次函数图象中用不同颜色笔标出y>0,y=0,y<0的部分。
根据你标的图象填空。
(1)-2x+6=0,即y=0,此时x=
。
(2)-2x+6>0,即y>0的图象在x轴的
方(填上方或下方),此时x
。
(3)-2x+6<0,即y<0的图象在x轴的
方(填上方或下方),此时x
。
总结:
当y=0时,图像正好与
轴相交
当y>0时,图像位于
轴
方
当y<0时,
图像位于
轴
方
通过上面的探究,你能说说一次函数与一元一次不等式有什么关系吗?与同伴交流一下。
师生活动:学生四人小组讨论交流3分钟后,汇报讨论结果.
总结:
求ax+b>0(或<0)(a,b是常数,a≠0)的解集
从数的角度:函数y=ax+b的函数值大于0(或小于0)时的x的取值范围
从形的角度:直线y=ax+b在X轴上方或下方时自变量的取值范围
点拨:这里体现了数学中的一种重要思想方法——数形结合法,帮助同学们直观的理解问题并解决问题.
探究二:
已知一次函数y=-2x+6的图象:
根据图象填空:
(1)-2x+6=4,即y=4,此时x=
.
(2)-2x+6>4,即y>4的图象在y=4的
方,此时x
.
(3)-2x+6<4,即y<4的图象在y=4的
方,此时x
.
(三)
典例学习
例1:根据函数图像直接写出不等式的解集
kx+b<0的解集是
x-2>0的解集是
例2:函数y=-3x+6,当x为何值时,对应的函数值y
(1)等于0?
(2)大于0?
(3)等于3?
(4)大于3?
(5)小于3?
例3.已知在同一坐标系上有一次函数y=3x+10和y=5x+4的图像。观察图像,回答问题
当x取何值时,y
=
y?
当x取何值时,y>
y?
当x取何值时,y
<y?
(四)
课堂小结
1.本节课学习了什么内容?
2.(1)利用一个一次函数图象解一元一次不等式
(2)利用同一坐标系上的两个一次函数图象解一元一次不等式
两种题型你会了吗?请总结解题方法
课后思考:用图像法解不等式x+2>0
作业布置
必做题:P108
第12题
选做题:P109
第13题,第14题
七.
板书设计
八.教学反思
一次函数与一元一次不等式
教学目标
知识与技能
理解一次函数与一元一次不等式之间的联系,会用函数观点得出一元一次不等式的解集
过程与方法
经历用函数图象表示不等式解集的过程,进一步体会数形结合思想.
情感态度与价值观
通过探究一次函数与一元一次不等式的联系,使学生感受数形结合思想的魅力,体会从不同角度认识事物本质的方法.
学情分析
八年级下的学生,具备了一定的推理能力和认知水平,掌握了基本的教学方法,但他们运用数学方法解决问题的能力不强,对知识的获取正处于从感性向理性转变的阶段.因此,在教学设计时,应遵循认知规律,由形象到抽象,由易到难,注重引导.
尽管学生已经掌握了方程、函数和不等式的相关知识,但这些知识是零散的,不能融会贯通,不能灵活运用知识选择最优方法来解决问题。第二,学生对数形结合方法的运用不够熟练,缺乏全面分析问题的能力。第三,不能准确的找到问题的本质特征。因此,找到一次函数与一元一次不等式之间的联系并准确的表述是本节课的难点。需要教师逐步引导.
教学重难点
重点:理解一次函数与一元一次不等式的联系
难点:把一次函数图象与一元一次不等式建立联系并能表述
突破难点:设计导学案让学生动手做一做,画一画,想一想,根据教师的引导发现并归纳结论.同时利用电子白板的写、画功能在电子白板上展示,直观形象进一步帮助学生理解.
四、教法与学法
教法:启发式教学,多媒体辅助
学法:独立思考,自主探究,合作交流
教学准备
多媒体课件
教学过程
课题引入
计算:
还有其他的方法吗?
如何利用函数图象来求解?
(设计意图)温故知新,在二元一次方程组的基础上引入新课,提出问题,引发学生思考.
(二
)
探究新知
探究一:
已知一次函数y=-2x+6的图象:
在一次函数图象中用不同颜色笔标出y>0,y=0,y<0的部分。
根据你标的图象填空。
(1)-2x+6=0,即y=0,此时x=
。
(2)-2x+6>0,即y>0的图象在x轴的
方(填上方或下方),此时x
。
(3)-2x+6<0,即y<0的图象在x轴的
方(填上方或下方),此时x
。
总结:
当y=0时,图像正好与
轴相交
当y>0时,图像位于
轴
方
当y<0时,
图像位于
轴
方
通过上面的探究,你能说说一次函数与一元一次不等式有什么关系吗?与同伴交流一下。
师生活动:学生四人小组讨论交流3分钟后,汇报讨论结果.
总结:
求ax+b>0(或<0)(a,b是常数,a≠0)的解集
从数的角度:函数y=ax+b的函数值大于0(或小于0)时的x的取值范围
从形的角度:直线y=ax+b在X轴上方或下方时自变量的取值范围
点拨:这里体现了数学中的一种重要思想方法——数形结合法,帮助同学们直观的理解问题并解决问题.
探究二:
已知一次函数y=-2x+6的图象:
根据图象填空:
(1)-2x+6=4,即y=4,此时x=
.
(2)-2x+6>4,即y>4的图象在y=4的
方,此时x
.
(3)-2x+6<4,即y<4的图象在y=4的
方,此时x
.
(三)
典例学习
例1:根据函数图像直接写出不等式的解集
kx+b<0的解集是
x-2>0的解集是
例2:函数y=-3x+6,当x为何值时,对应的函数值y
(1)等于0?
(2)大于0?
(3)等于3?
(4)大于3?
(5)小于3?
例3.已知在同一坐标系上有一次函数y=3x+10和y=5x+4的图像。观察图像,回答问题
当x取何值时,y
=
y?
当x取何值时,y>
y?
当x取何值时,y
<y?
(四)
课堂小结
1.本节课学习了什么内容?
2.(1)利用一个一次函数图象解一元一次不等式
(2)利用同一坐标系上的两个一次函数图象解一元一次不等式
两种题型你会了吗?请总结解题方法
课后思考:用图像法解不等式x+2>0
作业布置
必做题:P108
第12题
选做题:P109
第13题,第14题
七.
板书设计
八.教学反思
