人教版数学七年级下册 5.3 平行线的性质 课时复习同步练习含答案
文档属性
| 名称 | 人教版数学七年级下册 5.3 平行线的性质 课时复习同步练习含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 317.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 00:00:00 | ||
图片预览




文档简介
人教版数学七年级下册
5.3 平行线的性质
课时复习同步练习
一、选择题
1.如图5-3-1,直线a∥b,直线c与直线a,b相交,若∠1=56°,则∠2等于(
)
图5-3-1
A.24°
B.34°
C.56°
D.124°
2.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上,如果∠2=44°,那么∠1的度数是(
)
A.14°
B.15°
C.16°
D.17°
3.下列命题是真命题的是(
)
A.过直线外一点可以画无数条直线与已知直线平行
B.如果甲看乙的方向是北偏东60°,那么乙看甲的方向是南偏西30°
C.3条直线交于一点,对顶角最多有6对
D.与同一条直线相交的两条直线相交
4.如图,∠1=∠2,∠3=40°,则∠4等于(
)
A.120°
B.130°
C.140°
D.40°
5.如图,从三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为(
)
A.
0
B.
1
C.
2
D.
3
6.下列说法不正确的是(
)
A.证实命题正确与否的推理过程叫做证明
B.定理是命题,而且是真命题
C.“对顶角相等”是命题,但不是定理
D.要证明一个命题是假命题只要举出一个反例即可
7.某商品的商标可以抽象为如图所示的三条线段,若AB∥CD,∠EAB=45°,则∠FDC的度数是(
)
A.30°
B.45°
C.60°
D.75°
8.将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2;②∠3=∠4;③∠2+∠4=90°;④∠4+∠5=180°.其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
9.如图5-3-17,直线a,b被直线c所截,下列说法正确的是(
)
图5-3-17
A.当∠1=∠2时,一定有a∥b
B.当a∥b时,一定有∠1=∠2
C.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180°
时,一定有a∥b
10.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF=(
)
A.60°
B.65°
C.50°
D.45°
填空题
11.如图,直线AB∥CD,BC平分∠ABD.若∠1=54°,则∠2=________°.
12.?如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东
.
13.如图AC∥DF,AB∥EF,点D,E分别在AB,AC上,若∠2=50°,则∠1的度数为
.
14.
说明命题“x>-4,则x2>16”是假命题的一个反例可以是x=____________.
15.如图,若,则与的关系是________.
?
16.请写出命题“两直线平行,同位角相等”的题设和结论:
题设: ??????????????
,
结论: ??????????????
.
??
解答题
17.如图,某次考古发掘出的一块梯形残缺玉片,工作人员从玉片上量得∠A=115°,∠D=100°,已知梯形的两底AD∥BC,请你帮助工作人员求出另外两个角的度数,并说明理由.
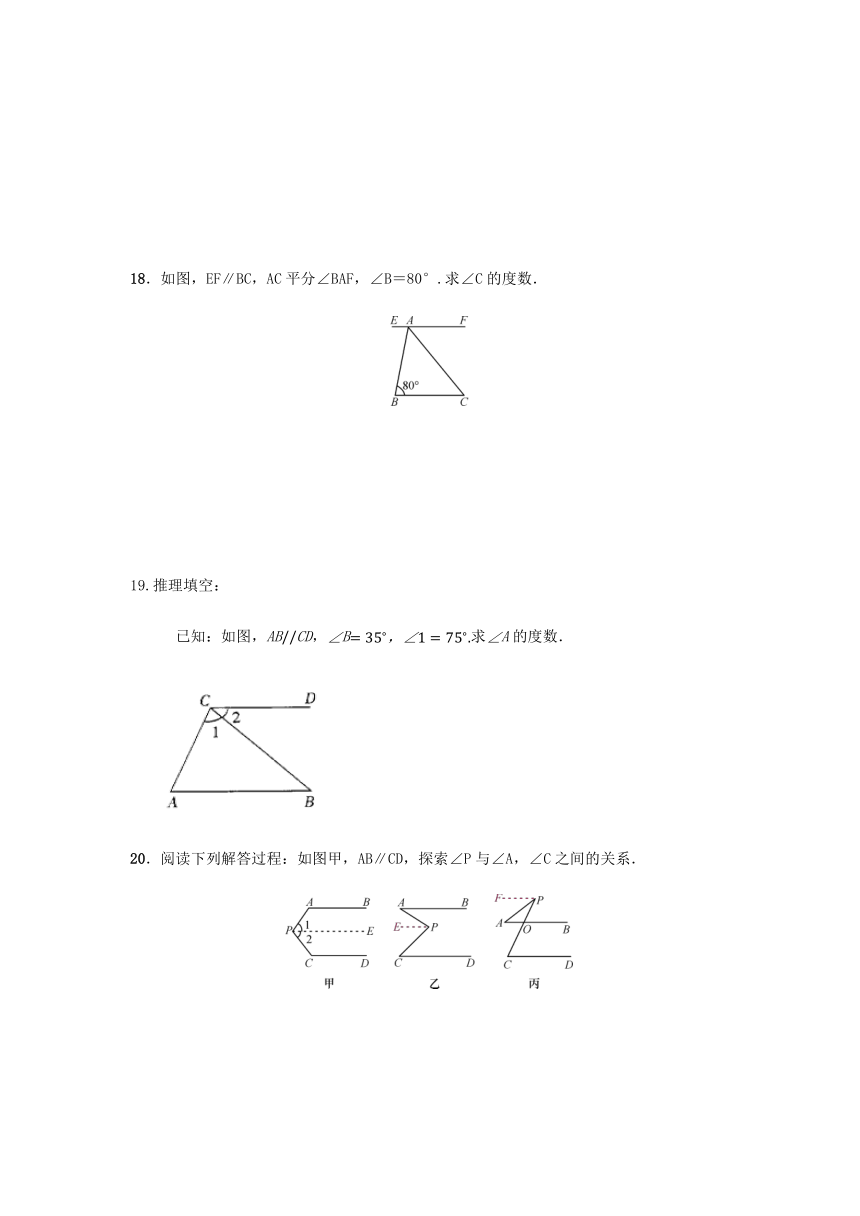
18.如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
19.推理填空:?
?已知:如图,ABCD,B求A的度数.
20.阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
参考答案:
一、选择题
1.如图5-3-1,直线a∥b,直线c与直线a,b相交,若∠1=56°,则∠2等于( C )
图5-3-1
A.24°
B.34°
C.56°
D.124°
2.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上,如果∠2=44°,那么∠1的度数是(
C
)
A.14°
B.15°
C.16°
D.17°
3.下列命题是真命题的是(
C )
A.过直线外一点可以画无数条直线与已知直线平行
B.如果甲看乙的方向是北偏东60°,那么乙看甲的方向是南偏西30°
C.3条直线交于一点,对顶角最多有6对
D.与同一条直线相交的两条直线相交
4.如图,∠1=∠2,∠3=40°,则∠4等于(
C
)
A.120°
B.130°
C.140°
D.40°
5.如图,从三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为(D)
A.
0
B.
1
C.
2
D.
3
6.下列说法不正确的是(
C
)
A.证实命题正确与否的推理过程叫做证明
B.定理是命题,而且是真命题
C.“对顶角相等”是命题,但不是定理
D.要证明一个命题是假命题只要举出一个反例即可
7.某商品的商标可以抽象为如图所示的三条线段,若AB∥CD,∠EAB=45°,则∠FDC的度数是(
B
)
A.30°
B.45°
C.60°
D.75°
8.将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2;②∠3=∠4;③∠2+∠4=90°;④∠4+∠5=180°.其中正确的有(
D
)
A.1个
B.2个
C.3个
D.4个
9.如图5-3-17,直线a,b被直线c所截,下列说法正确的是( D
)
图5-3-17
A.当∠1=∠2时,一定有a∥b
B.当a∥b时,一定有∠1=∠2
C.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180°
时,一定有a∥b
10.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF=(A
)
A.60°
B.65°
C.50°
D.45°
填空题
11.如图,直线AB∥CD,BC平分∠ABD.若∠1=54°,则∠2=________°.
【答案】72
12.?如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东
.
【答案】42°
13.如图AC∥DF,AB∥EF,点D,E分别在AB,AC上,若∠2=50°,则∠1的度数为
.
【答案】50°
14.
说明命题“x>-4,则x2>16”是假命题的一个反例可以是x=____________.
【答案】
-3(答案不唯一)
15.如图,若,则与的关系是________.
【答案】相等??
16.请写出命题“两直线平行,同位角相等”的题设和结论:
题设: ??????????????
,
结论: ??????????????
.
【答案】两直线平行;被第三条直线截得的同位角相等??
解答题
17.如图,某次考古发掘出的一块梯形残缺玉片,工作人员从玉片上量得∠A=115°,∠D=100°,已知梯形的两底AD∥BC,请你帮助工作人员求出另外两个角的度数,并说明理由.
解:∵AD∥BC,∠A=115°,∠D=100°,
∴∠B=180°-∠A=180°-115°=65°,
∠C=180°-∠D=180°-100°=80°.
18.如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
解:∵EF∥BC,
∴∠BAF=180°-∠B=100°(两直线平行,同旁内角互补).
∵AC平分∠BAF,
∴∠CAF=∠BAF=50°.
∵EF∥BC,
∴∠C=∠CAF=50°(两直线平行,内错角相等).
19.推理填空:?
?已知:如图,ABCD,B求A的度数.
解题思路分析:欲求A,只要求ACD的大小.
解:CDAB,B已知
_______________________,____________
?而ACD______.
?
CDAB,??
已知??
?
A______?
____________
,____________?
?
A_______.
解:已知
两直线平行,内错角相等
?而110.
?
??
已知??
?
ACD?
两直线平行,同旁内角互补
?
70
故答案为:B;35;两直线平行?
内错角相等;110;;
??????
两直线平行同旁内角互补;.
20.阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
解:如图乙,过点P作PE∥AB.
∵AB∥CD(已知),
∴PE∥AB∥CD(平行于同一条直线的两条直线平行).
∴∠A=∠EPA,∠EPC=∠C(两直线平行,内错角相等).
∵∠APC=∠EPA+∠EPC,
∴∠APC=∠A+∠C(等量代换).
如图丙,过点P作PF∥AB.
∴∠FPA=∠A(两直线平行,内错角相等).
∵AB∥CD(已知),
∴PF∥CD(平行于同一条直线的两条直线平行).
∴∠FPC=∠C(两直线平行,内错角相等).
∵∠FPC-∠FPA=∠APC,
∴∠C-∠A=∠APC(等量代换).
5.3 平行线的性质
课时复习同步练习
一、选择题
1.如图5-3-1,直线a∥b,直线c与直线a,b相交,若∠1=56°,则∠2等于(
)
图5-3-1
A.24°
B.34°
C.56°
D.124°
2.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上,如果∠2=44°,那么∠1的度数是(
)
A.14°
B.15°
C.16°
D.17°
3.下列命题是真命题的是(
)
A.过直线外一点可以画无数条直线与已知直线平行
B.如果甲看乙的方向是北偏东60°,那么乙看甲的方向是南偏西30°
C.3条直线交于一点,对顶角最多有6对
D.与同一条直线相交的两条直线相交
4.如图,∠1=∠2,∠3=40°,则∠4等于(
)
A.120°
B.130°
C.140°
D.40°
5.如图,从三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为(
)
A.
0
B.
1
C.
2
D.
3
6.下列说法不正确的是(
)
A.证实命题正确与否的推理过程叫做证明
B.定理是命题,而且是真命题
C.“对顶角相等”是命题,但不是定理
D.要证明一个命题是假命题只要举出一个反例即可
7.某商品的商标可以抽象为如图所示的三条线段,若AB∥CD,∠EAB=45°,则∠FDC的度数是(
)
A.30°
B.45°
C.60°
D.75°
8.将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2;②∠3=∠4;③∠2+∠4=90°;④∠4+∠5=180°.其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
9.如图5-3-17,直线a,b被直线c所截,下列说法正确的是(
)
图5-3-17
A.当∠1=∠2时,一定有a∥b
B.当a∥b时,一定有∠1=∠2
C.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180°
时,一定有a∥b
10.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF=(
)
A.60°
B.65°
C.50°
D.45°
填空题
11.如图,直线AB∥CD,BC平分∠ABD.若∠1=54°,则∠2=________°.
12.?如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东
.
13.如图AC∥DF,AB∥EF,点D,E分别在AB,AC上,若∠2=50°,则∠1的度数为
.
14.
说明命题“x>-4,则x2>16”是假命题的一个反例可以是x=____________.
15.如图,若,则与的关系是________.
?
16.请写出命题“两直线平行,同位角相等”的题设和结论:
题设: ??????????????
,
结论: ??????????????
.
??
解答题
17.如图,某次考古发掘出的一块梯形残缺玉片,工作人员从玉片上量得∠A=115°,∠D=100°,已知梯形的两底AD∥BC,请你帮助工作人员求出另外两个角的度数,并说明理由.
18.如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
19.推理填空:?
?已知:如图,ABCD,B求A的度数.
20.阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
参考答案:
一、选择题
1.如图5-3-1,直线a∥b,直线c与直线a,b相交,若∠1=56°,则∠2等于( C )
图5-3-1
A.24°
B.34°
C.56°
D.124°
2.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上,如果∠2=44°,那么∠1的度数是(
C
)
A.14°
B.15°
C.16°
D.17°
3.下列命题是真命题的是(
C )
A.过直线外一点可以画无数条直线与已知直线平行
B.如果甲看乙的方向是北偏东60°,那么乙看甲的方向是南偏西30°
C.3条直线交于一点,对顶角最多有6对
D.与同一条直线相交的两条直线相交
4.如图,∠1=∠2,∠3=40°,则∠4等于(
C
)
A.120°
B.130°
C.140°
D.40°
5.如图,从三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为(D)
A.
0
B.
1
C.
2
D.
3
6.下列说法不正确的是(
C
)
A.证实命题正确与否的推理过程叫做证明
B.定理是命题,而且是真命题
C.“对顶角相等”是命题,但不是定理
D.要证明一个命题是假命题只要举出一个反例即可
7.某商品的商标可以抽象为如图所示的三条线段,若AB∥CD,∠EAB=45°,则∠FDC的度数是(
B
)
A.30°
B.45°
C.60°
D.75°
8.将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2;②∠3=∠4;③∠2+∠4=90°;④∠4+∠5=180°.其中正确的有(
D
)
A.1个
B.2个
C.3个
D.4个
9.如图5-3-17,直线a,b被直线c所截,下列说法正确的是( D
)
图5-3-17
A.当∠1=∠2时,一定有a∥b
B.当a∥b时,一定有∠1=∠2
C.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180°
时,一定有a∥b
10.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF=(A
)
A.60°
B.65°
C.50°
D.45°
填空题
11.如图,直线AB∥CD,BC平分∠ABD.若∠1=54°,则∠2=________°.
【答案】72
12.?如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东
.
【答案】42°
13.如图AC∥DF,AB∥EF,点D,E分别在AB,AC上,若∠2=50°,则∠1的度数为
.
【答案】50°
14.
说明命题“x>-4,则x2>16”是假命题的一个反例可以是x=____________.
【答案】
-3(答案不唯一)
15.如图,若,则与的关系是________.
【答案】相等??
16.请写出命题“两直线平行,同位角相等”的题设和结论:
题设: ??????????????
,
结论: ??????????????
.
【答案】两直线平行;被第三条直线截得的同位角相等??
解答题
17.如图,某次考古发掘出的一块梯形残缺玉片,工作人员从玉片上量得∠A=115°,∠D=100°,已知梯形的两底AD∥BC,请你帮助工作人员求出另外两个角的度数,并说明理由.
解:∵AD∥BC,∠A=115°,∠D=100°,
∴∠B=180°-∠A=180°-115°=65°,
∠C=180°-∠D=180°-100°=80°.
18.如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
解:∵EF∥BC,
∴∠BAF=180°-∠B=100°(两直线平行,同旁内角互补).
∵AC平分∠BAF,
∴∠CAF=∠BAF=50°.
∵EF∥BC,
∴∠C=∠CAF=50°(两直线平行,内错角相等).
19.推理填空:?
?已知:如图,ABCD,B求A的度数.
解题思路分析:欲求A,只要求ACD的大小.
解:CDAB,B已知
_______________________,____________
?而ACD______.
?
CDAB,??
已知??
?
A______?
____________
,____________?
?
A_______.
解:已知
两直线平行,内错角相等
?而110.
?
??
已知??
?
ACD?
两直线平行,同旁内角互补
?
70
故答案为:B;35;两直线平行?
内错角相等;110;;
??????
两直线平行同旁内角互补;.
20.阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
解:如图乙,过点P作PE∥AB.
∵AB∥CD(已知),
∴PE∥AB∥CD(平行于同一条直线的两条直线平行).
∴∠A=∠EPA,∠EPC=∠C(两直线平行,内错角相等).
∵∠APC=∠EPA+∠EPC,
∴∠APC=∠A+∠C(等量代换).
如图丙,过点P作PF∥AB.
∴∠FPA=∠A(两直线平行,内错角相等).
∵AB∥CD(已知),
∴PF∥CD(平行于同一条直线的两条直线平行).
∴∠FPC=∠C(两直线平行,内错角相等).
∵∠FPC-∠FPA=∠APC,
∴∠C-∠A=∠APC(等量代换).
