沪教版高中数学高二下册:11.4点到直线的距离 课件(共17张PPT)
文档属性
| 名称 | 沪教版高中数学高二下册:11.4点到直线的距离 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 874.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第十一章 坐标平面上的直线
11.4.1
点到直线的距离
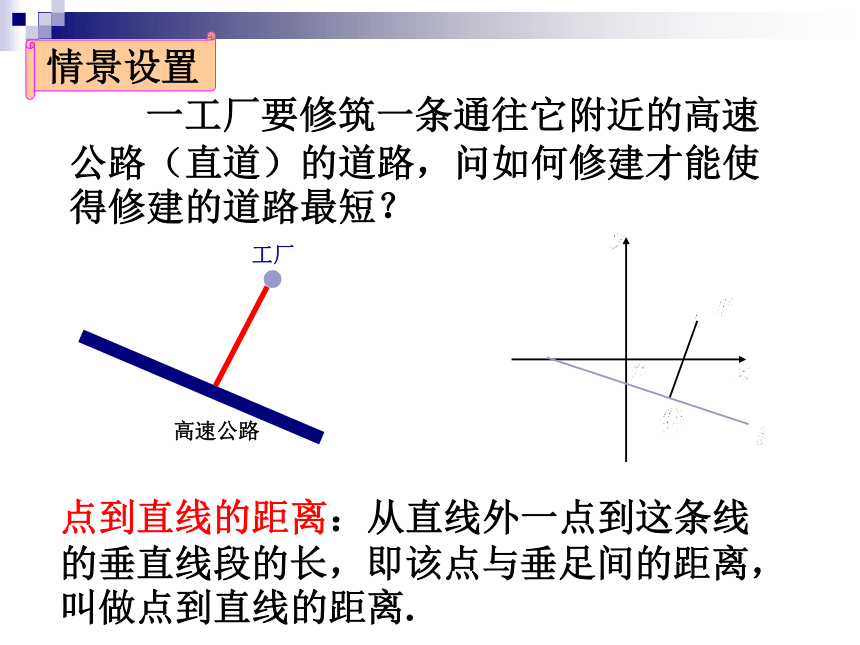
一工厂要修筑一条通往它附近的高速公路(直道)的道路,问如何修建才能使得修建的道路最短?
点到直线的距离:从直线外一点到这条线的垂直线段的长,即该点与垂足间的距离,叫做点到直线的距离.
情景设置
已知点
,直线
求点
到直线
的距离
已知点
,直线
求点
到直线
的距离
一、点到直线的距离公式
点
到直线
的距离为
此公式称为点到直线的距离公式
例1.求点
及原点到下列直线的距离:
(1)
(2)
解:
(1)由点到直线的距离公式,得
(2)直线与
轴平行,因此
例2.求平行直线
之间的距离.
分析:转化为点到直线的距离.
解:在直线
上取点
则点
到直线
的距离就是这两条
平行线间的距离.
思考
下面两条平行直线如何求距离?
二、平行直线的距离公式
平行直线
间的距离为
课堂练习
求下列平行线之间的距离:
(1)
(2)
课堂小结:
4.已知
的三个顶点坐标分别为
5.直线过原点,且点
到直线的距离为
,
求该直线的方程.
,求
边上的高的长度.
3.求与直线
平行且距离等于2的直线
的方程.
课堂练习
课堂练习
1.求点
到直线
的距离:
(1)
(2)
(3)
(4)
2.求下列平行线之间的距离:
(1)
(2)
课堂练习答案
1.(1)
(2)
(3)
(4)
2.(1)
(2)
3.解:设所求直线方程为
解得
因此所求直线为
课堂练习答案
4.解:
,因此利用向量投影
5.解:直线斜率存在时,设直线方程为
即
,根据条件有
又直线
也符合条件,因此所求直线
方程为
或
课外阅读材料
点到直线距离公式的几
种证明方法
1.利用两点距离公式
已知直线
及定点
垂足
①
②
①2+
②2
即得:
课外阅读材料
点到直线距离公式的几
种证明方法
2.利用向量投影
已知直线
及定点
垂足
设
为直线上任意一点
因为
,所以:
课外阅读材料
点到直线距离公式的几
种证明方法
3.利用直角三角形(限定
)
已知直线
及定点
垂足
构造
把
代入即得
①
①
第十一章 坐标平面上的直线
11.4.1
点到直线的距离
一工厂要修筑一条通往它附近的高速公路(直道)的道路,问如何修建才能使得修建的道路最短?
点到直线的距离:从直线外一点到这条线的垂直线段的长,即该点与垂足间的距离,叫做点到直线的距离.
情景设置
已知点
,直线
求点
到直线
的距离
已知点
,直线
求点
到直线
的距离
一、点到直线的距离公式
点
到直线
的距离为
此公式称为点到直线的距离公式
例1.求点
及原点到下列直线的距离:
(1)
(2)
解:
(1)由点到直线的距离公式,得
(2)直线与
轴平行,因此
例2.求平行直线
之间的距离.
分析:转化为点到直线的距离.
解:在直线
上取点
则点
到直线
的距离就是这两条
平行线间的距离.
思考
下面两条平行直线如何求距离?
二、平行直线的距离公式
平行直线
间的距离为
课堂练习
求下列平行线之间的距离:
(1)
(2)
课堂小结:
4.已知
的三个顶点坐标分别为
5.直线过原点,且点
到直线的距离为
,
求该直线的方程.
,求
边上的高的长度.
3.求与直线
平行且距离等于2的直线
的方程.
课堂练习
课堂练习
1.求点
到直线
的距离:
(1)
(2)
(3)
(4)
2.求下列平行线之间的距离:
(1)
(2)
课堂练习答案
1.(1)
(2)
(3)
(4)
2.(1)
(2)
3.解:设所求直线方程为
解得
因此所求直线为
课堂练习答案
4.解:
,因此利用向量投影
5.解:直线斜率存在时,设直线方程为
即
,根据条件有
又直线
也符合条件,因此所求直线
方程为
或
课外阅读材料
点到直线距离公式的几
种证明方法
1.利用两点距离公式
已知直线
及定点
垂足
①
②
①2+
②2
即得:
课外阅读材料
点到直线距离公式的几
种证明方法
2.利用向量投影
已知直线
及定点
垂足
设
为直线上任意一点
因为
,所以:
课外阅读材料
点到直线距离公式的几
种证明方法
3.利用直角三角形(限定
)
已知直线
及定点
垂足
构造
把
代入即得
①
①
