人教版数学七年级下册5.1 相交线课件(15张)
文档属性
| 名称 | 人教版数学七年级下册5.1 相交线课件(15张) |  | |
| 格式 | zip | ||
| 文件大小 | 177.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-02 22:31:00 | ||
图片预览



文档简介
(共15张PPT)
第五章
相交线与平行线
5.1
相交线
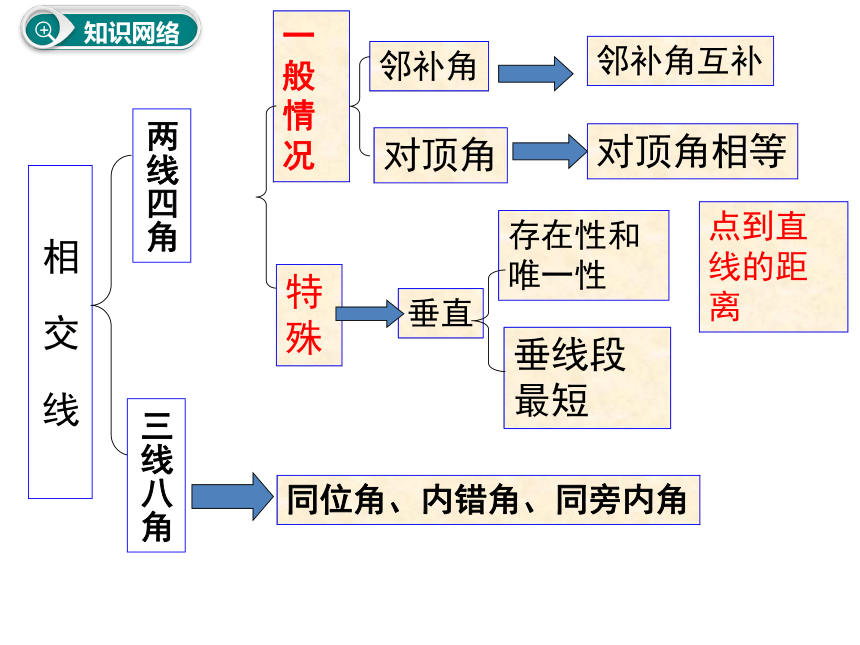
知识网络
相
交
线
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
特殊
垂直
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
三线八角
两线四角
1
2
3
A
B
C
D
O
1
邻补角:如果两个角有一条公共边,它们的另一边互为____________,那么这两个角互为邻补角.图中∠1的邻补角有___________.
反向延长线
∠2,
∠3
一、两条直线相交
2、邻补角互补
∠2+∠3=1800
1
3
A
B
C
D
O
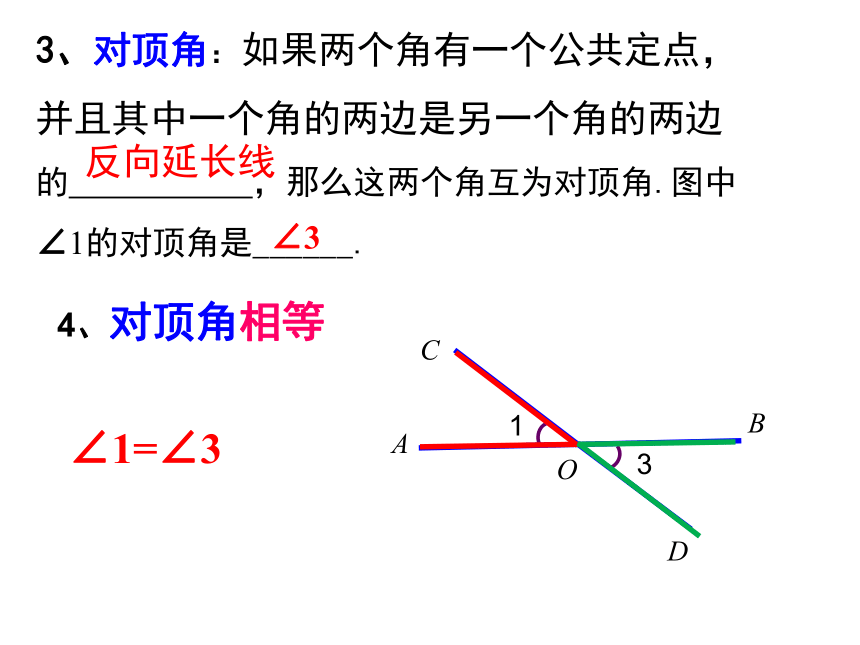
3、对顶角:如果两个角有一个公共定点,并且其中一个角的两边是另一个角的两边的
,那么这两个角互为对顶角.图中∠1的对顶角是______.
反向延长线
∠3
4、对顶角相等
∠1=∠3
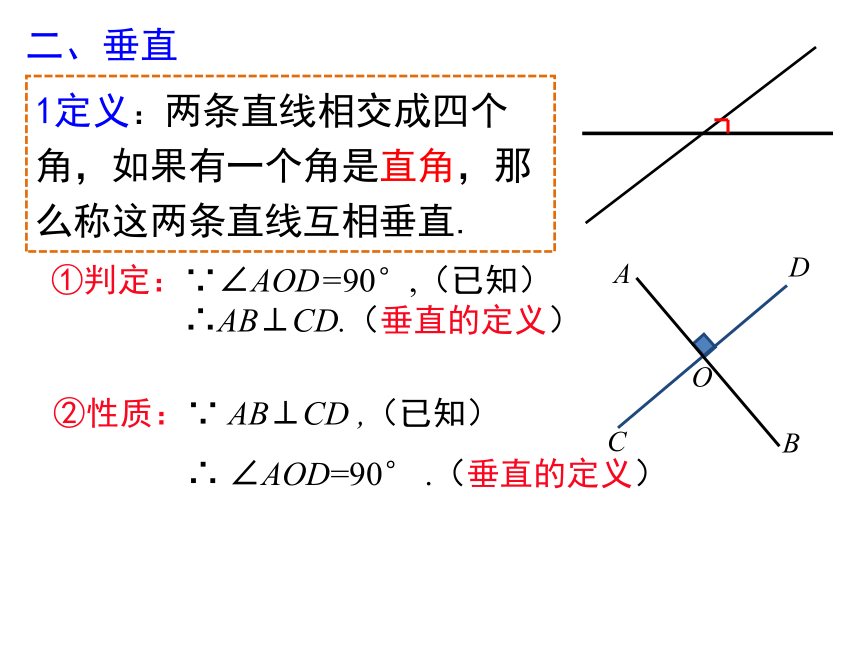
1定义:两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直.
二、垂直
①判定:∵∠AOD=90°,(已知)
∴AB⊥CD.(垂直的定义)
②性质:∵
AB⊥CD
,(已知)
∴
∠AOD=90°
.(垂直的定义)
A
B
C
D
O
1、在同一平面内,过一点有且只有一条直线与已知直线垂直.
2、连接直线外一点与直线上各点的所有线段中垂线段最短.简单说成:垂线段最短.
3、垂线的性质:
2、垂线的画法
4、
点到直线的距离
6
7
5
8
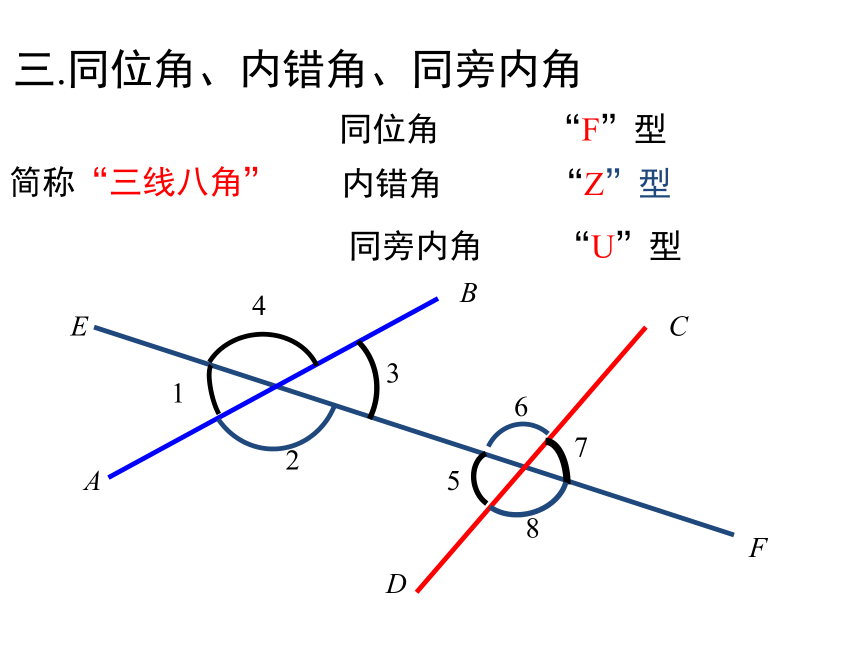
简称“三线八角”
B
A
F
E
C
D
4
3
1
2
三.同位角、内错角、同旁内角
同位角
“F”型
内错角
“Z”型
同旁内角
“U”型
1.如图,直线AB、CD、EF相交,若∠1
+∠5=180°,找出图中与∠1
相等的角.
D
B
E
O
A
C
F
解:∵
∠1=
∠3(对顶角相等)
1
2
3
4
5
6
8
7
∠5+∠8=180
°且∠1
+∠5=180°
∴∠8=
∠1
∵
∠8=
∠6(对顶角相等)
∴∠6=
∠1.
2.如图,直线AB、CD、EF、MN相交,若∠2=∠5,找出图中与∠2
互补的角.
F
N
C
E
A
B
D
M
1
2
3
4
5
8
6
7
解:∵
∠1+∠2=180°
∠2+∠3=
180°
∴∠2的补角有∠1和∠3
∵
∠5+∠8=180°,
∠5+∠6=180
°且∠2=∠5
∴∠2的补角有∠6和∠8
3(1)如图1,若直线m、n相交于点O,∠1=90°,则
;
(2)若直线AB、CD相交于点O,且AB⊥CD,则
∠BOD
=______;
(3)如图2,BO⊥AO,∠BOC与∠BOA的度数之比
为1∶5,那么∠COA=____,∠BOC的补角为
.
O
m
n
1
B
C
A
O
m⊥n
90°
72°
162°
图1
图2
4、如图,直线BC与MN相交于点O,AO⊥BC,∠BOE=∠NOE,若∠EON=20°,求∠AOM和∠NOC的度数.
解:∵∠BOE=∠NOE,
∴∠BON=2∠EON=40°,
∴∠NOC=180°-∠BON
=180°-40°=140°,
∠MOC=∠BON=40°.
∵AO⊥BC,
∴∠AOC=90°,
∴∠AOM=∠AOC-∠MOC=90°-40°=50°,
∴∠NOC=140°,∠AOM=50°.
(1)如图1,若ED,BF被AB所截,则∠1与____是同位角.
5.看图填空:
∠2
(2)如图2,若ED,BC被AF所截,则∠3与___
是内错角.
∠4
图1
图2
(3)如图3,∠1与∠3是AB和AF被_____所截构成的
角;
DE
内错
(4)如图4,∠2与∠4是
和
被BC所截构成的____角.
AB
AF
同位
图3
图4
拓展题:观察下列各图,寻找对顶角(不含平角)
⑴
如图a,图中共有
对对顶角;
⑵
如图b,图中共有
对对顶角;
⑶
如图c,图中共有
对对顶角;
⑷
研究⑴~⑶小题中直线条数与对顶角的对数之间的关系,猜测:若有n条直线相交于一点,则可形成
对对顶角;
⑸
若有10条直线相交于一点,则可形成
对对顶角.
图a
图b
图c
2
6
12
n(n-1)
90
作业:
第五章
相交线与平行线
5.1
相交线
知识网络
相
交
线
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
特殊
垂直
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
三线八角
两线四角
1
2
3
A
B
C
D
O
1
邻补角:如果两个角有一条公共边,它们的另一边互为____________,那么这两个角互为邻补角.图中∠1的邻补角有___________.
反向延长线
∠2,
∠3
一、两条直线相交
2、邻补角互补
∠2+∠3=1800
1
3
A
B
C
D
O
3、对顶角:如果两个角有一个公共定点,并且其中一个角的两边是另一个角的两边的
,那么这两个角互为对顶角.图中∠1的对顶角是______.
反向延长线
∠3
4、对顶角相等
∠1=∠3
1定义:两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直.
二、垂直
①判定:∵∠AOD=90°,(已知)
∴AB⊥CD.(垂直的定义)
②性质:∵
AB⊥CD
,(已知)
∴
∠AOD=90°
.(垂直的定义)
A
B
C
D
O
1、在同一平面内,过一点有且只有一条直线与已知直线垂直.
2、连接直线外一点与直线上各点的所有线段中垂线段最短.简单说成:垂线段最短.
3、垂线的性质:
2、垂线的画法
4、
点到直线的距离
6
7
5
8
简称“三线八角”
B
A
F
E
C
D
4
3
1
2
三.同位角、内错角、同旁内角
同位角
“F”型
内错角
“Z”型
同旁内角
“U”型
1.如图,直线AB、CD、EF相交,若∠1
+∠5=180°,找出图中与∠1
相等的角.
D
B
E
O
A
C
F
解:∵
∠1=
∠3(对顶角相等)
1
2
3
4
5
6
8
7
∠5+∠8=180
°且∠1
+∠5=180°
∴∠8=
∠1
∵
∠8=
∠6(对顶角相等)
∴∠6=
∠1.
2.如图,直线AB、CD、EF、MN相交,若∠2=∠5,找出图中与∠2
互补的角.
F
N
C
E
A
B
D
M
1
2
3
4
5
8
6
7
解:∵
∠1+∠2=180°
∠2+∠3=
180°
∴∠2的补角有∠1和∠3
∵
∠5+∠8=180°,
∠5+∠6=180
°且∠2=∠5
∴∠2的补角有∠6和∠8
3(1)如图1,若直线m、n相交于点O,∠1=90°,则
;
(2)若直线AB、CD相交于点O,且AB⊥CD,则
∠BOD
=______;
(3)如图2,BO⊥AO,∠BOC与∠BOA的度数之比
为1∶5,那么∠COA=____,∠BOC的补角为
.
O
m
n
1
B
C
A
O
m⊥n
90°
72°
162°
图1
图2
4、如图,直线BC与MN相交于点O,AO⊥BC,∠BOE=∠NOE,若∠EON=20°,求∠AOM和∠NOC的度数.
解:∵∠BOE=∠NOE,
∴∠BON=2∠EON=40°,
∴∠NOC=180°-∠BON
=180°-40°=140°,
∠MOC=∠BON=40°.
∵AO⊥BC,
∴∠AOC=90°,
∴∠AOM=∠AOC-∠MOC=90°-40°=50°,
∴∠NOC=140°,∠AOM=50°.
(1)如图1,若ED,BF被AB所截,则∠1与____是同位角.
5.看图填空:
∠2
(2)如图2,若ED,BC被AF所截,则∠3与___
是内错角.
∠4
图1
图2
(3)如图3,∠1与∠3是AB和AF被_____所截构成的
角;
DE
内错
(4)如图4,∠2与∠4是
和
被BC所截构成的____角.
AB
AF
同位
图3
图4
拓展题:观察下列各图,寻找对顶角(不含平角)
⑴
如图a,图中共有
对对顶角;
⑵
如图b,图中共有
对对顶角;
⑶
如图c,图中共有
对对顶角;
⑷
研究⑴~⑶小题中直线条数与对顶角的对数之间的关系,猜测:若有n条直线相交于一点,则可形成
对对顶角;
⑸
若有10条直线相交于一点,则可形成
对对顶角.
图a
图b
图c
2
6
12
n(n-1)
90
作业:
