人教A版高中数学必修4第二章第三节2.3.3平面向量的坐标运算(共20张PPT)
文档属性
| 名称 | 人教A版高中数学必修4第二章第三节2.3.3平面向量的坐标运算(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 655.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
2.3.3
《平面向量的坐标运算》
学习目标
掌握平面向量和、差、积的坐标运算;理解向量的坐标与端点的坐标换算,会用向量的运算求多边形在平面直角坐标系中的坐标。
教学重点
会用坐标表示平面向量的加、减及数乘的坐标运算.
教学难点
向量的坐标表示的理解及运算的准确性.
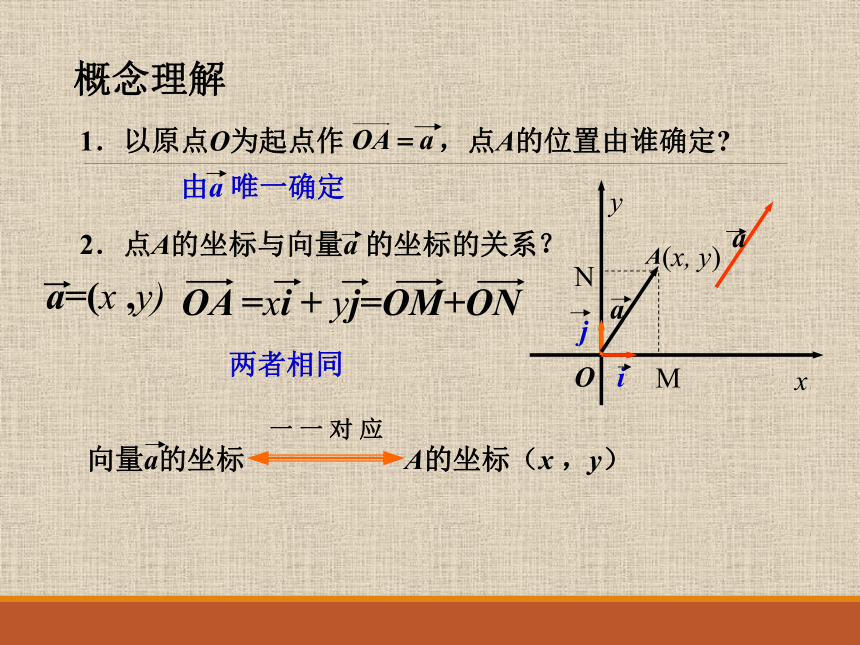
平面向量的坐标表示
有且只有一对实数x、y,使得
(x,y)叫做向量a的坐标,记作
两者相同
一
一
对
应
概念理解
(x,
y)
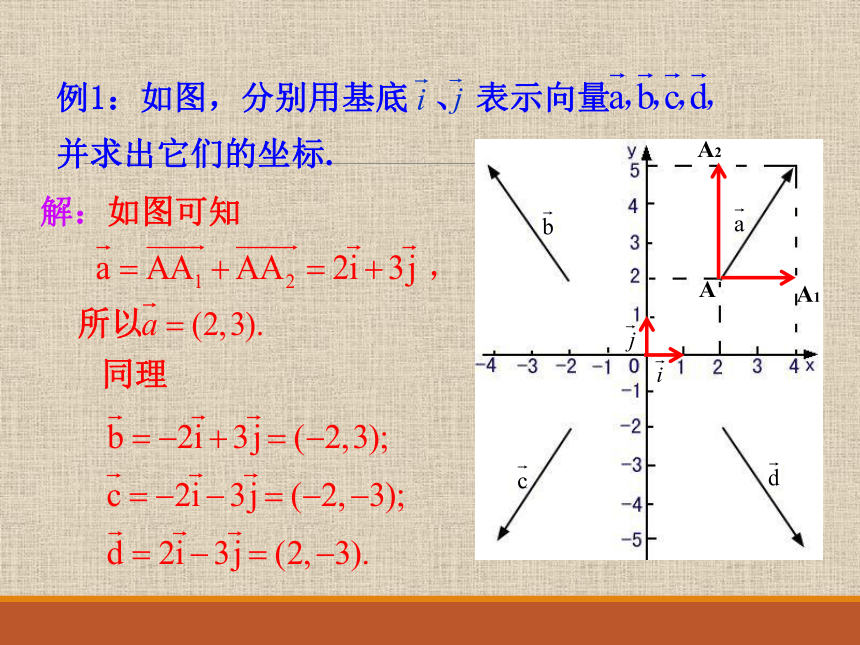
例1:如图,分别用基底
、
表示向量
并求出它们的坐标.
A
A1
A2
解:如图可知
同理
由向量线性运算的结合律和分配律可得
课堂探究
平面向量的坐标运算
两个向量和(差)的坐标分别等于这两个向量相应坐标的和(差).
实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标.
即
同理可得
这就是说,
已知a=(x,y)和实数λ,那么
这就是说,
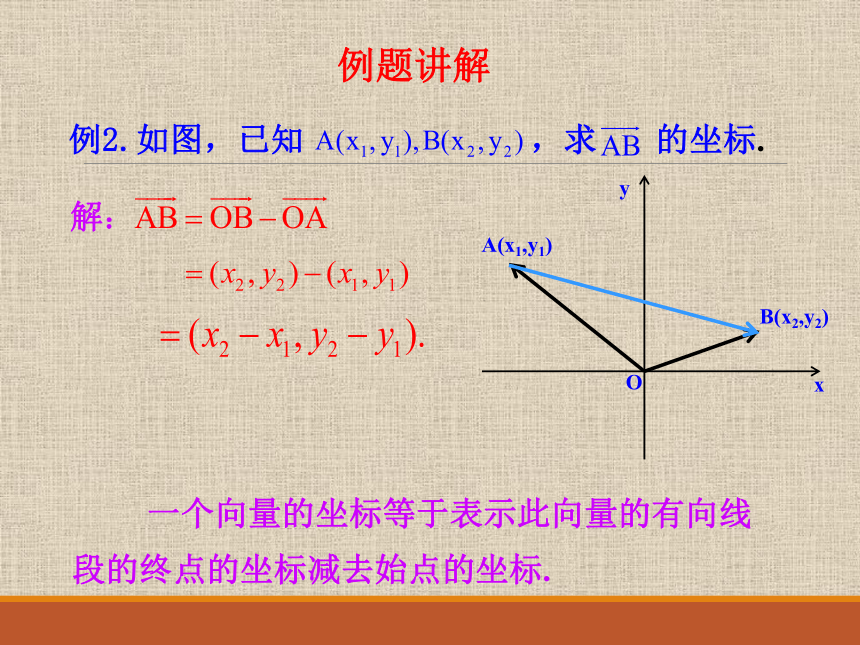
结论:
一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标。
如图,已知A(x1,y1),B(x2,y2),
根据上面的结论,有
AB=
OB
-
OA
=
(x2,y2)
-
(x1,y1)
=
(x2-x1,y2-y1)
例2.如图,已知
,求
的坐标.
x
y
O
B(x2,y2)
A(x1,y1)
解:
一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标.
例题讲解
小结:平面向量的坐标运算
例2.已知
,求
的坐标.
例3
已知平行四边形ABCD的三个定点A、B、C的坐标分别为(-2,1)、(-1,3)、(3,4),求顶点D的坐标
则点B的坐标为_________.
(5,4)
1.已知A(3,1),
,若向量
,
O为坐标原点,则x=________,y=_________.
-4
5
2.
3、已知向量a=(-2,3),b∥a,向量b
起点为A(1,2),终点B在坐标轴上,求点B的坐标。
4:下列向量组中,能作为表示它们所在平面内所有向量的基底,正确的有(
)
(1)e1=(
-1
,
2
),e2=(
5
,
7
)
(2)e1=(
3
,
5
),e2=(
6
,
10
)
(3)e1=(
2
,
-3
),e2=(
1/2
,
-3/4
)
5.已知:点A(2,3),B(5,4),C(7,10),若
,试求λ为何值时,
(1)点P在一、三象限角平分线上?
(2)点P在第三象限内?
(1)若点P在一、三象限角平分线上,
则
5+5λ=4+7λ,
(2)若点P在第三象限内,
所以λ<-1,即只要λ<-1,点P就在第三象限内.
一、知识技能
2.平面向量的坐标运算
二、思想方法
数形结合思想、分类讨论思想、方程思想.
1.平面向量的坐标表示
补充说明:
1.
向量的坐标运算是根据向量的坐标表示和向量的线性运算律得出的结论,它符合实数的运算规律,并使得向量的运算完全代数化.
2.对于两个非零向量共线的坐标表示,可借助斜率相等来理解和记忆.
3.利用向量的坐标运算,可以求点的坐标,判断点共线等问题,这是一种向量方法,体现了向量的工具作用.
2.3.3
《平面向量的坐标运算》
学习目标
掌握平面向量和、差、积的坐标运算;理解向量的坐标与端点的坐标换算,会用向量的运算求多边形在平面直角坐标系中的坐标。
教学重点
会用坐标表示平面向量的加、减及数乘的坐标运算.
教学难点
向量的坐标表示的理解及运算的准确性.
平面向量的坐标表示
有且只有一对实数x、y,使得
(x,y)叫做向量a的坐标,记作
两者相同
一
一
对
应
概念理解
(x,
y)
例1:如图,分别用基底
、
表示向量
并求出它们的坐标.
A
A1
A2
解:如图可知
同理
由向量线性运算的结合律和分配律可得
课堂探究
平面向量的坐标运算
两个向量和(差)的坐标分别等于这两个向量相应坐标的和(差).
实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标.
即
同理可得
这就是说,
已知a=(x,y)和实数λ,那么
这就是说,
结论:
一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标。
如图,已知A(x1,y1),B(x2,y2),
根据上面的结论,有
AB=
OB
-
OA
=
(x2,y2)
-
(x1,y1)
=
(x2-x1,y2-y1)
例2.如图,已知
,求
的坐标.
x
y
O
B(x2,y2)
A(x1,y1)
解:
一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标.
例题讲解
小结:平面向量的坐标运算
例2.已知
,求
的坐标.
例3
已知平行四边形ABCD的三个定点A、B、C的坐标分别为(-2,1)、(-1,3)、(3,4),求顶点D的坐标
则点B的坐标为_________.
(5,4)
1.已知A(3,1),
,若向量
,
O为坐标原点,则x=________,y=_________.
-4
5
2.
3、已知向量a=(-2,3),b∥a,向量b
起点为A(1,2),终点B在坐标轴上,求点B的坐标。
4:下列向量组中,能作为表示它们所在平面内所有向量的基底,正确的有(
)
(1)e1=(
-1
,
2
),e2=(
5
,
7
)
(2)e1=(
3
,
5
),e2=(
6
,
10
)
(3)e1=(
2
,
-3
),e2=(
1/2
,
-3/4
)
5.已知:点A(2,3),B(5,4),C(7,10),若
,试求λ为何值时,
(1)点P在一、三象限角平分线上?
(2)点P在第三象限内?
(1)若点P在一、三象限角平分线上,
则
5+5λ=4+7λ,
(2)若点P在第三象限内,
所以λ<-1,即只要λ<-1,点P就在第三象限内.
一、知识技能
2.平面向量的坐标运算
二、思想方法
数形结合思想、分类讨论思想、方程思想.
1.平面向量的坐标表示
补充说明:
1.
向量的坐标运算是根据向量的坐标表示和向量的线性运算律得出的结论,它符合实数的运算规律,并使得向量的运算完全代数化.
2.对于两个非零向量共线的坐标表示,可借助斜率相等来理解和记忆.
3.利用向量的坐标运算,可以求点的坐标,判断点共线等问题,这是一种向量方法,体现了向量的工具作用.
