2020年人教版九年级数学下册 名校入学考试数学试卷(含详细解答)
文档属性
| 名称 | 2020年人教版九年级数学下册 名校入学考试数学试卷(含详细解答) |  | |
| 格式 | zip | ||
| 文件大小 | 662.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-01 22:57:45 | ||
图片预览




文档简介
人教版九年级数学下册
名校入学考试校考卷
一、选择题:(本大题12个小题,每小题4分,共48分)每个小题都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案的代号填入答题卡上对应位置中.
1.已知△ABC中,AC=4,BC=3,AB=5,则sinA=( )
A.
B.
C.
D.
2.用配方法解方程x2+4x﹣5=0,下列配方正确的是( )
A.(x+2)2=1
B.(x+2)2=5
C.(x+2)2=9
D.(x+4)2=9
3.下列式子,正确的是( )
A.3+=3
B.(
+1)(﹣1)=1
C.2﹣1=﹣2
D.x2+2xy﹣y2=(x﹣y)2
4.在?ABCD中,若∠A:∠B=1:2,则∠A的度数是( )
A.60°
B.90°
C.120°
D.150°
5.已知一个等腰三角形的两条边长分别为3和8,则这个等腰三角形的周长为( )
A.11
B.14
C.19
D.14或19
6.二次函数y=﹣2(x﹣4)2﹣5的开口方向、对称轴分别是( )
A.开口向上、直线x=﹣4
B.开口向上、直线x=4
C.开口向下、直线x=﹣4
D.开口向下、直线x=4
7.如图,在⊙O中,∠AOB=50°,则∠ACB=( )
A.30°
B.25°
C.50°
D.40°
8.如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )
A.30°
B.45°
C.55°
D.75°
9.某校九年级(1)班有7个合作学习小组,各学习小组的人数分别为:5,6,6,x,7,8,9,已知这组数据的平均数是7,则这组数据的中位数是( )
A.6
B.7
C.8
D.9
10.下列图形都是由几个黑色和白色的正方形按一定规律组成,图①中有2个黑色正方形,图②中有5个黑色正方形,图③中有8个黑色正方形,图④中有11个黑色正方形,…,依次规律,图⑩中黑色正方形的个数是
( )
A.32
B.29
C.28
D.26
11.如图,在平面直角坐标系中,将矩形OABC沿对角线OB对折,使点A(,0)落在点A1处,已知点B的坐标是(,1),则点A1的坐标是( )
A.(,)
B.(,)
C.(,2)
D.(,)
12.如图,在平面直角坐标系系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=在第一象限内的图象交于点B,连接B0.若S△OBC=1,tan∠BOC=,则k2的值是( )
A.﹣3
B.1
C.2
D.3
二.填空(本大题6个小题,每小题4分共24分)
13.方程(x﹣2)2=4的根是 .
14.计算:2cos60°﹣tan45°= .
15.已知一个菱形的两条对角线长分别为6cm和8cm,则这个菱形的面积为 cm2.
16.在某时刻的阳光照耀下,身高160cm的阿美的影长为80cm,她身旁的旗杆影长5m,则旗杆高为 m.
17.从﹣1,0,1,2,3这五个数中,随机抽取一个数记为m,则使关于x的不等式组有解,并且使函数y=(m﹣1)x2+2mx+m+2与x轴有交点的概率为 .
18.在?ABCD中,AB<BC,已知∠B=30°,AB=2,将△ABC沿AC翻折至△AB′C,使点B′落在?ABCD所在的平面内,连接B′D.若△AB′D是直角三角形,则BC的长为 .
三.解答题(本大题2小题,每小题7分,共14分)解答时每小题必须给出必要的演算过程或推理步骤.
19.解二元一次方程组.
20.为有效开展阳光体育活动,云洱中学利用课外活动时间进行班级篮球比赛,每场比赛都要决出胜负,每队胜一场得2分,负一场得1分.已知九年级一班在8场比赛中得到13分,问九年级一班胜、负场数分别是多少?
四、解答题:(本大题4个小题,每小题10分,共40分,解答题时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线).)
21.先化简,再求值:(﹣)÷,其中x=tan60°+2.
22.2015年1月,市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价.评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查,了解他们每天在课外用于学习的时间,并绘制成如下不完整的统计图.
根据上述信息,解答下列问题:
(1)本次抽取的学生人数是 ;扇形统计图中的圆心角α等于 ;补全统计直方图;
(2)被抽取的学生还要进行一次50米跑测试,每5人一组进行.在随机分组时,小红、小花两名女生被分到同一个小组,请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率.
23.“村村通公路”工程是国家为支持新农村建设的一项重大举措,为了落实这一举措,重庆潼南县政府计划在南北方向的A、B两村之间建一条公路AB.已知公路AB的一侧有C村,在公路AB上的M处测得C村在M的南偏东37°方向上,从M向南走270米到达N处,测得C村在N的东南方向上,且C村周围800米范围内为油菜花田,那么计划修建的公路AB是否会穿过油菜花田,请说明理由(参考数据:sin37°≈0.8,cos37°≈0.8,tan37°≈0.75)
24.长宽比为(n为正整数)的矩形称为矩形.下面,我们通过折叠的方式折出一个矩形,如图①所示.
操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.
操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.
则四边形BCEF为矩形.
证明:设正方形ABCD的边长为1,则BD=.
由折叠性质可知BG=BC=1,∠AFE=∠BFE=90°,则四边形BCEF为矩形.
∴∠A=∠BFE.∴EF∥AD.
∴,即,∴.∴.
∴四边形BCEF为矩形.
阅读以上内容,回答下列问题:
(1)在图①中,所有与CH相等的线段是 ,tan∠HBC的值是 ;
(2)已知四边形BCEF为矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN为矩形;
(3)将图②中的矩形BCMN沿用(2)中的方式操作3次后,得到一个“矩形”,则n的值是 .
五、解答题(本大题2个小题,每小题12分,共24分)解答时每小题都必须写出必要的演算过程或推理步骤,请将解答过程书写在答卷中对应的位置上.
25.已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE′,连接EE′.
(1)如图1,∠AEE′= °;
(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;
(3)如图3,在(2)的条件下,如果CE=2,AE=,求ME的长.
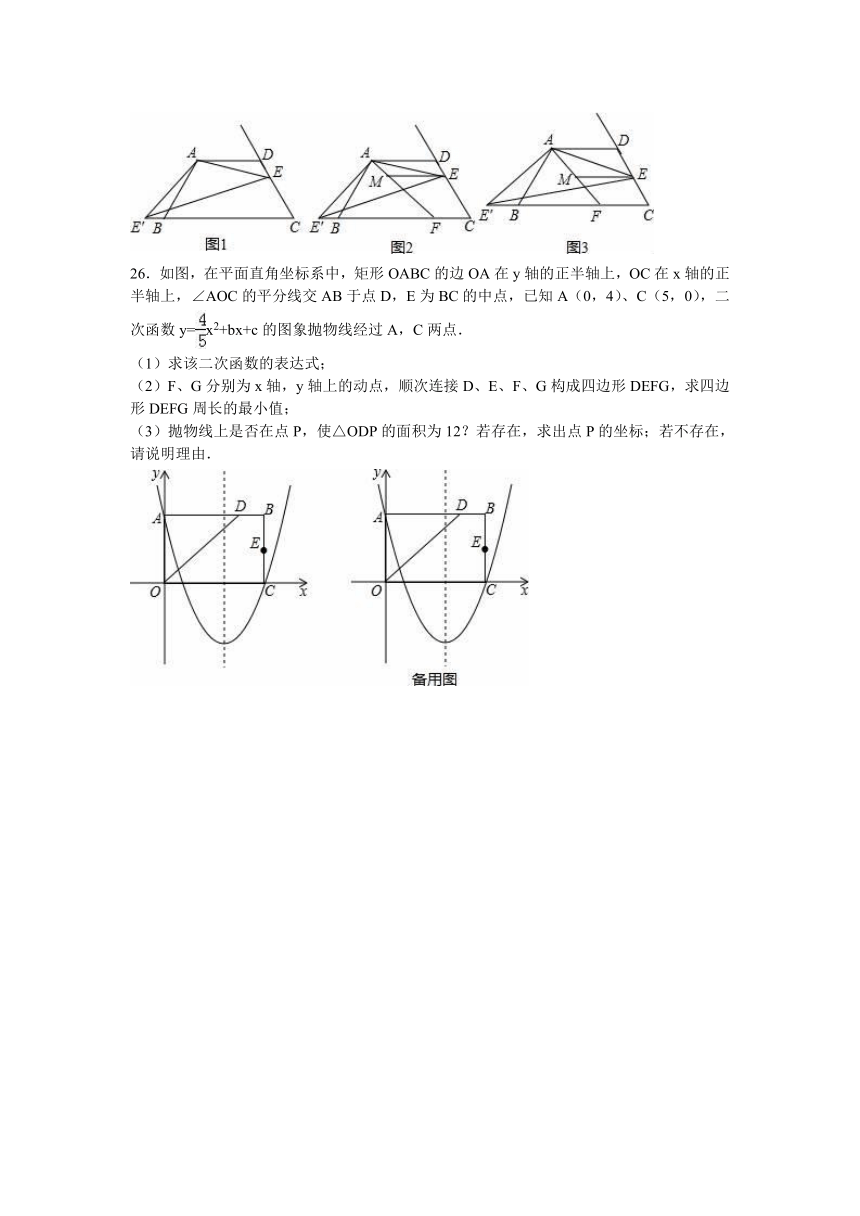
26.如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,∠AOC的平分线交AB于点D,E为BC的中点,已知A(0,4)、C(5,0),二次函数y=x2+bx+c的图象抛物线经过A,C两点.
(1)求该二次函数的表达式;
(2)F、G分别为x轴,y轴上的动点,顺次连接D、E、F、G构成四边形DEFG,求四边形DEFG周长的最小值;
(3)抛物线上是否在点P,使△ODP的面积为12?若存在,求出点P的坐标;若不存在,请说明理由.
2015-2016年九年级(下)入学考试数学试卷
参考答案与试题解析
一、选择题:(本大题12个小题,每小题4分,共48分)每个小题都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案的代号填入答题卡上对应位置中.
1.已知△ABC中,AC=4,BC=3,AB=5,则sinA=( )
A.
B.
C.
D.
【考点】锐角三角函数的定义;勾股定理的逆定理.
【分析】先根据直角三角形的三边长判断出三角形的形状,再根据锐角三角函数的定义求解即可.
【解答】解:∵△ABC中,AC=4,BC=3,AB=5,即42+32=52,
∴△ABC是直角三角形,∠C=90°.
sinA==.
故选A.
2.用配方法解方程x2+4x﹣5=0,下列配方正确的是( )
A.(x+2)2=1
B.(x+2)2=5
C.(x+2)2=9
D.(x+4)2=9
【考点】解一元二次方程-配方法.
【分析】先将原方程进行配方,然后选项进行对照,即可得到正确选项.
【解答】解:x2+4x﹣5=0,
配方,得
(x+2)2=9.
故选C.
3.下列式子,正确的是( )
A.3+=3
B.(
+1)(﹣1)=1
C.2﹣1=﹣2
D.x2+2xy﹣y2=(x﹣y)2
【考点】二次根式的乘除法;负整数指数幂.
【分析】根据二次根式的加减、负整数指数幂和完全平方公式判断.
【解答】解:A、不是同类二次根式,不能相加,故错误;
B、正确;
C、原式=,故错误;
D、与完全平方公式不符,故错误.
故选B.
4.在?ABCD中,若∠A:∠B=1:2,则∠A的度数是( )
A.60°
B.90°
C.120°
D.150°
【考点】平行四边形的性质.
【分析】根据平行四边形的基本性质可知,平行四边形的邻角互补,由已知可得,∠A、∠B是邻角,故∠A可求解.
【解答】解:∵?ABCD,
∴∠A+∠B=180°,
而∠A:∠B=1:2
∴∠A=60°,∠B=120°
∴∠A=60°.
故选A.
5.已知一个等腰三角形的两条边长分别为3和8,则这个等腰三角形的周长为( )
A.11
B.14
C.19
D.14或19
【考点】等腰三角形的性质;三角形三边关系.
【分析】分3是腰长与底边长两种情况讨论求解即可.
【解答】解:①3是腰长时,三角形的三边分别为3、3、8,
∵3+3=6<8,
∴此时不能组成三角形;
②3是底边长时,三角形的三边分别为3、8、8,
此时能组成三角形,
所以,周长=3+8+8=19,
综上所述,这个等腰三角形的周长是19.
故选C.
6.二次函数y=﹣2(x﹣4)2﹣5的开口方向、对称轴分别是( )
A.开口向上、直线x=﹣4
B.开口向上、直线x=4
C.开口向下、直线x=﹣4
D.开口向下、直线x=4
【考点】二次函数的性质.
【分析】已知抛物线解析式为顶点式,可根据顶点式求抛物线的开口方向,对称轴.
【解答】解:由y=﹣2(x﹣4)2﹣5可知,二次项系数为﹣2<0,
∴抛物线开口向下,对称轴为直线x=4,
故选D.
7.如图,在⊙O中,∠AOB=50°,则∠ACB=( )
A.30°
B.25°
C.50°
D.40°
【考点】圆周角定理.
【分析】直接根据圆周角定理求解即可.
【解答】解:∠ACB=∠AOB=×50°=25°.
故选:B.
8.如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )
A.30°
B.45°
C.55°
D.75°
【考点】线段垂直平分线的性质;等腰三角形的性质.
【分析】根据等腰三角形的性质得到∠A=∠ACB=75°,根据线段垂直平分线的性质得到BD=CD,求得∠DCE=∠B=30°,即可得到结论.
【解答】解:∵AB=BC,∠B=30°,
∴∠A=∠ACB=75°,
∵DE垂直平分BC,
∴BD=CD,
∴∠DCE=∠B=30°,
∴∠ACD=∠ACB=∠DCB=45°,
故选B.
9.某校九年级(1)班有7个合作学习小组,各学习小组的人数分别为:5,6,6,x,7,8,9,已知这组数据的平均数是7,则这组数据的中位数是( )
A.6
B.7
C.8
D.9
【考点】中位数;算术平均数.
【分析】根据题意首先求出x的值,再利用中位数的定义求出答案.
【解答】解:∵5,6,6,x,7,8,9,这组数据的平均数是7,
∴5+6+6+x+7+8+9=7×7,
解得:x=8,
故这组数据按从小到大排列:5,6,6,7,8,8,9,
则这组数据的中位数是:7.
故选:B.
10.下列图形都是由几个黑色和白色的正方形按一定规律组成,图①中有2个黑色正方形,图②中有5个黑色正方形,图③中有8个黑色正方形,图④中有11个黑色正方形,…,依次规律,图⑩中黑色正方形的个数是
( )
A.32
B.29
C.28
D.26
【考点】规律型:图形的变化类.
【分析】仔细观察图形,找到图形的个数与黑色正方形的个数的通项公式后代入n=11后即可求解.
【解答】解:观察图形发现:
图①中有2个黑色正方形,
图②中有2+3×(2﹣1)=5个黑色正方形,
图③中有2+3(3﹣1)=8个黑色正方形,
图④中有2+3(4﹣1)=11个黑色正方形,
…,
图n中有2+3(n﹣1)=3n﹣1个黑色的正方形,
当n=10时,2+3×(10﹣1)=29,
故选B.
11.如图,在平面直角坐标系中,将矩形OABC沿对角线OB对折,使点A(,0)落在点A1处,已知点B的坐标是(,1),则点A1的坐标是( )
A.(,)
B.(,)
C.(,2)
D.(,)
【考点】翻折变换(折叠问题);坐标与图形性质.
【分析】由已知可得∠AOB=30°,翻折后找到相等的角及相等的边,在直角三角形中,利用勾股定理可求得答案.
【解答】解:过A1作A1D⊥OA,
∵A(,0),B的坐标是(,1),
∴OA=,AB=1,
在Rt△OAB中,OB==2,AB=1,
∴AB=OB,
∵△AOB是直角三角形,
∴∠AOB=30°,
OB为折痕,
∴∠A1OB=∠AOB=30°,OA1=OA=,
Rt△OA1D中,∠OA1D=30°,
∴OD=×=,
A1D=×=,
∴点A1的坐标(,).
故选B.
12.如图,在平面直角坐标系系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=在第一象限内的图象交于点B,连接B0.若S△OBC=1,tan∠BOC=,则k2的值是( )
A.﹣3
B.1
C.2
D.3
【考点】反比例函数与一次函数的交点问题.
【分析】首先根据直线求得点C的坐标,然后根据△BOC的面积求得BD的长,然后利用正切函数的定义求得OD的长,从而求得点B的坐标,求得结论.
【解答】解:∵直线y=k1x+2与x轴交于点A,与y轴交于点C,
∴点C的坐标为(0,2),
∴OC=2,
∵S△OBC=1,
∴BD=1,
∵tan∠BOC=,
∴=,
∴OD=3,
∴点B的坐标为(1,3),
∵反比例函数y=在第一象限内的图象交于点B,
∴k2=1×3=3.
故选D.
二.填空(本大题6个小题,每小题4分共24分)
13.方程(x﹣2)2=4的根是 4,0 .
【考点】解一元二次方程-直接开平方法.
【分析】根据方程的特点,用直接开平方法解一元二次方程即可.
【解答】解:(x﹣2)2=4,
x﹣2=±2,
解得:x1=4,x2=0.
故答案为:4,0.
14.计算:2cos60°﹣tan45°= 0 .
【考点】特殊角的三角函数值.
【分析】将特殊角的三角函数值直接代入即可求解.
【解答】解:2cos60°﹣tan45°=2×﹣1=0.
15.已知一个菱形的两条对角线长分别为6cm和8cm,则这个菱形的面积为 24 cm2.
【考点】菱形的性质.
【分析】根据菱形的面积等于两对角线乘积的一半求得其面积即可.
【解答】解:∵一个菱形的两条对角线长分别为6cm和8cm,
∴这个菱形的面积=×6×8=24(cm2).
故答案为:24.
16.在某时刻的阳光照耀下,身高160cm的阿美的影长为80cm,她身旁的旗杆影长5m,则旗杆高为 10 m.
【考点】相似三角形的应用.
【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.
【解答】解:根据相同时刻的物高与影长成比例,设旗杆的高度为x
m,则
160:80=x:5,
解得x=10.
故答案是:10.
17.从﹣1,0,1,2,3这五个数中,随机抽取一个数记为m,则使关于x的不等式组有解,并且使函数y=(m﹣1)x2+2mx+m+2与x轴有交点的概率为 .
【考点】概率公式;解一元一次不等式组;抛物线与x轴的交点.
【分析】首先解不等式以及利用二次函数与x轴交点个数和△的关系分别得出m的取值范围,进而利用概率公式求出即可.
【解答】解:∵x+1≤m,解得;x≤m﹣1,
2﹣x≤2m,解得:x≥2﹣2m,
∴使关于x的不等式组有解,则m﹣1≥2﹣2m,
解得:m≥1,
∵使函数y=(m﹣1)x2+2mx+m+2与x轴有交点,
∴b2﹣4ac4m2﹣4(m﹣1)(m+2)=﹣4m+8≥0,
解得:m≤2,
∴m的取值范围是:1≤m≤2,
∴从﹣1,0,1,2,3这五个数中,随机抽取一个数记为m,符合题意的有1,2,
故使关于x的不等式组有解,并且使函数y=(m﹣1)x2+2mx+m+2与x轴有交点的概率为.
故答案为:.
18.在?ABCD中,AB<BC,已知∠B=30°,AB=2,将△ABC沿AC翻折至△AB′C,使点B′落在?ABCD所在的平面内,连接B′D.若△AB′D是直角三角形,则BC的长为 4或6 .
【考点】翻折变换(折叠问题);平行四边形的性质.
【分析】在?ABCD中,AB<BC,要使△AB′D是直角三角形,有两种情况:∠B′AD=90°或∠AB′D=90°,画出图形,分类讨论即可.
【解答】解:当∠B′AD=90°AB<BC时,如图1,
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AD∥BC,∠B′AD=90°,
∴∠B′GC=90°,
∵∠B=30°,AB=2,
∴∠AB′C=30°,
∴GC=
B′C=
BC,
∴G是BC的中点,
在Rt△ABG中,BG=AB=×2=3,
∴BC=6;
当∠AB′D=90°时,如图2,
∵AD=BC,BC=B′C,
∴AD=B′C,
∵由折叠的性质:∠BAC=90°,
∴AC∥B′D,
∴四边形ACDB′是等腰梯形,
∵∠AB′D=90°,
∴四边形ACDB′是矩形,
∴∠BAC=90°,
∵∠B=30°,AB=2,
∴BC=AB÷=2×=4,
∴当BC的长为4或6时,△AB′D是直角三角形.
故答案为:4或6.
三.解答题(本大题2小题,每小题7分,共14分)解答时每小题必须给出必要的演算过程或推理步骤.
19.解二元一次方程组.
【考点】解二元一次方程组.
【分析】方程组利用加减消元法求出解即可.
【解答】解:②﹣①得:5y=5,即y=1,
把y=1代入①得:x=3,
则方程组的解为.
20.为有效开展阳光体育活动,云洱中学利用课外活动时间进行班级篮球比赛,每场比赛都要决出胜负,每队胜一场得2分,负一场得1分.已知九年级一班在8场比赛中得到13分,问九年级一班胜、负场数分别是多少?
【考点】一元一次方程的应用.
【分析】设胜了x场,那么负了(8﹣x)场,根据得分为13分可列方程求解.
【解答】解:设胜了x场,那么负了(8﹣x)场,根据题意得:
2x+1?(8﹣x)=13,
x=5,
8﹣5=3.
答:九年级一班胜、负场数分别是5和3.
四、解答题:(本大题4个小题,每小题10分,共40分,解答题时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线).)
21.先化简,再求值:(﹣)÷,其中x=tan60°+2.
【考点】分式的化简求值;特殊角的三角函数值.
【分析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
【解答】解:原式=[﹣]?=?=?=,
当x=tan60°+2=+2时,原式=.
22.2015年1月,市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价.评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查,了解他们每天在课外用于学习的时间,并绘制成如下不完整的统计图.
根据上述信息,解答下列问题:
(1)本次抽取的学生人数是 30 ;扇形统计图中的圆心角α等于 144° ;补全统计直方图;
(2)被抽取的学生还要进行一次50米跑测试,每5人一组进行.在随机分组时,小红、小花两名女生被分到同一个小组,请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率.
【考点】列表法与树状图法;扇形统计图;利用频率估计概率.
【分析】(1)根据题意列式求值,根据相应数据画图即可;
(2)根据题意列表,然后根据表中数据求出概率即可.
【解答】解:(1)6÷20%=30,(30﹣3﹣7﹣6﹣2)÷30×360=12÷30×26=144°,
答:本次抽取的学生人数是30人;扇形统计图中的圆心角α等于144°;
故答案为:30,144°;
补全统计图如图所示:
(2)根据题意列表如下:
设竖列为小红抽取的跑道,横排为小花抽取的跑道,
小红
小花
1
2
3
4
5
1
(2,1)
(3,1)
(4,1)
(5,1)
2
(1,2)
(3,2)
(4,2)
(5,2)
3
(1,3)
(2,3)
(4,3)
(5,3)
4
(1,4)
(2,4)
(3,4)
(5,4)
5
(1,5)
(2,5)
(3,5)
(4,5)
记小红和小花抽在相邻两道这个事件为A,
∴.
23.“村村通公路”工程是国家为支持新农村建设的一项重大举措,为了落实这一举措,重庆潼南县政府计划在南北方向的A、B两村之间建一条公路AB.已知公路AB的一侧有C村,在公路AB上的M处测得C村在M的南偏东37°方向上,从M向南走270米到达N处,测得C村在N的东南方向上,且C村周围800米范围内为油菜花田,那么计划修建的公路AB是否会穿过油菜花田,请说明理由(参考数据:sin37°≈0.8,cos37°≈0.8,tan37°≈0.75)
【考点】解直角三角形的应用-方向角问题.
【分析】本题要求的实际上是C到AB的距离,过C点作CD⊥AB,CD就是所求的线段,由于CD是条公共直角边,可用CD表示出MD,ND,然后根据MN的长,来求出CD的长.
【解答】解:如图,过C点作CD⊥AB于D,
由题可知:∠CND=45°,∠CMD=37°.
设CD=x千米,tan∠CMD=,
则MD=.
tan∠CND=,
则ND==x,
∵MN=270米,
∴MD﹣ND=MN,即tan37°x﹣x=270,
∴﹣x=270,
解得
x=810.
∵810米>800米,
∴计划修建的公路AB是不会穿过油菜花田.
答:计划修建的公路AB是不会穿过油菜花田.
24.长宽比为(n为正整数)的矩形称为矩形.下面,我们通过折叠的方式折出一个矩形,如图①所示.
操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.
操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.
则四边形BCEF为矩形.
证明:设正方形ABCD的边长为1,则BD=.
由折叠性质可知BG=BC=1,∠AFE=∠BFE=90°,则四边形BCEF为矩形.
∴∠A=∠BFE.∴EF∥AD.
∴,即,∴.∴.
∴四边形BCEF为矩形.
阅读以上内容,回答下列问题:
(1)在图①中,所有与CH相等的线段是 GH、DG ,tan∠HBC的值是 ﹣1 ;
(2)已知四边形BCEF为矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN为矩形;
(3)将图②中的矩形BCMN沿用(2)中的方式操作3次后,得到一个“矩形”,则n的值是 6 .
【考点】几何变换综合题.
【分析】(1)设CH=GH=DG=x,根据DC=DH+CH=1,列出方程即可求出HC,然后运用三角函数的定义求出tan∠HBC的值.
(2)只需借鉴阅读中证明“四边形BCEF为矩形”的方法就可解决问题.
(3)利用(2)中结论,寻找规律可得到n的值.
【解答】解:(1)如图①中,由折叠可得:
DG=HG,GH=CH,
∴DG=GH=CH.
设HC=x,则DG=GH=x.
∵∠DGH=90°,
∴DH=x,
∴DC=DH+CH=x+x=1,
解得x=﹣1.
∴tan∠HBC===﹣1.
故答案为:GH、DG,;
(2)如图②中,∵BC=1,EC=BF=,
∴BE==
由折叠可得BP=BC=1,∠FNM=∠BNM=90°,∠EMN=∠CMN=90°.
∵四边形BCEF是矩形,
∴∠F=∠FEC=∠C=∠FBC=90°,
∴四边形BCMN是矩形,∠BNM=∠F=90°,
∴MN∥EF,
∴=,
即BP?BF=BE?BN,
∴1×=BN,
∴BN=,
∴BC:BN=1:
=:1,
∴四边形BCMN是的矩形;
(3)同理可得:
将矩形沿用(2)中的方式操作1次后,得到一个“矩形”,
将矩形沿用(2)中的方式操作1次后,得到一个“矩形”,
将矩形沿用(2)中的方式操作1次后,得到一个“矩形”,
所以将图②中的矩形BCMN沿用(2)中的方式操作3次后,得到一个“矩形”.
故答案为6.
五、解答题(本大题2个小题,每小题12分,共24分)解答时每小题都必须写出必要的演算过程或推理步骤,请将解答过程书写在答卷中对应的位置上.
25.已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE′,连接EE′.
(1)如图1,∠AEE′= 30 °;
(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;
(3)如图3,在(2)的条件下,如果CE=2,AE=,求ME的长.
【考点】几何变换综合题.
【分析】(1)根据旋转性质以及三角形内角和定理即可解决.
(2)根据EM∥FE′可以得==,再根据AN=NE,BE′=DE即可得到线段DE、BF、ME之间的关系.
(3)通过辅助线求出线段E′F=7,E′Q=9,再由(2)的结论得到ME的长.
【解答】解:(1)∵△ABE′是由△ADE绕点A顺时针旋转120°得到,
∴∠EAE′=120°,AE=AE′,
∴∠E′=∠AEE′==30°,
故答案为30°.
(2)①当点E在CD上时,DE+BF=2ME,理由如下:
如图1,当点E在线段CD上,AF交EE′于N,
∵∠EAF=30°,∠EAE′=120,
∴∠E′AN=90°,
∴E′N=2AN,
∵∠NAE=∠NEA=30°,
∴NA=NE,E′N=2EN,
∵EM∥FE′,
∴==,
∵BE′=DE,
∴E′F=2ME,
∴DE+BF=2ME.
②当点E在CD延长线上,0°<∠EAD∠30°时,BF﹣DE=2ME,理由如下:
如图2,∵∠EAF=30°,∠EAE′=120,
∴∠E′AN=90°,
∴E′N=2AN,
∵∠NAE=∠NEA=30°,
∴NA=NE,E′N=2EN,
∵EM∥FE′,
∴==,
∵BE′=DE,
∴E′F=2ME,
∴BF﹣DE=2ME.
③当30°<∠EAD∠90°时,DE+BF=2ME,理由如下:
如图3,∵∠EAM=30°,∠EAE′=120,
∴∠E′AN=90°,
∴E′N=2AN,
∵∠NAE=∠NEA=30°,
∴NA=NE,E′N=2EN,
∵EM∥FE′,
∴==,
∵BE′=DE,
∴E′F=2ME,
∴BF+DE=2ME.
④当90°<∠EAD<120°时,DE﹣BF=2ME,理由如下:
如图4,∵∠EAM=30°,∠EAE′=120,
∴∠E′AN=90°,
∴E′N=2AN,
∵∠NAE=∠NEA=30°,
∴NA=NE,E′N=2EN,
∵EM∥FE′,
∴==,
∵BE′=DE,
∴E′F=2ME,
∴DE﹣BF=2ME.
(3)如图5,作AG⊥BC于点G,DH⊥BC于H,AP⊥EE′于P,EQ⊥BC于Q,
∵AD∥BC,AD=AB=CD,∠BAD=120°,易知四边形AGHD是矩形,
在△AGB和△DHC中,
,
∴△AGB≌△DHC,
∴BG=HC,AD=GH,
∵∠ABE′=∠ADC=120°,
∴点E′、B、C共线,设AD=AB=CD=x,则GH=x,BG=CH=x,
在RT△EQC中,CE=2,∠ECQ=60°,
∴CQ=EC=1,EQ=,
∴E′Q=BC+BE′﹣CQ=3x﹣3,
在RT△APE中,AE=2,∠AEP=30°,
∴AP=,PE=,
∵AE=AE′,AP⊥EE′,
∴PE=PE′=,
∴EE′=2,
在RT△E′EQ中,E′Q==9,
∴3x﹣3=9,
∴x=4,
∴DE=BE′=2,BC=8,BG=2,
∴E′G=4,
∵∠AE′G=′AE′F,∠AGE′=∠FAE′,
∴△AGE′∽△FAE′,
∴,
∴,
∴E′F=7,
∴BF=E′F﹣E′B=7﹣2=5,
∵DE+BF=2ME
∴ME=.
26.如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,∠AOC的平分线交AB于点D,E为BC的中点,已知A(0,4)、C(5,0),二次函数y=x2+bx+c的图象抛物线经过A,C两点.
(1)求该二次函数的表达式;
(2)F、G分别为x轴,y轴上的动点,顺次连接D、E、F、G构成四边形DEFG,求四边形DEFG周长的最小值;
(3)抛物线上是否在点P,使△ODP的面积为12?若存在,求出点P的坐标;若不存在,请说明理由.
【考点】二次函数综合题.
【分析】(1)根据待定系数法,可得函数解析式;
(2)延长EC至E′,使E′C=EC,延长DA至D′,使D′A=DA,连接D′E′,交x轴于F点,交y轴于G点,则有:GD=GD′,EF=E′F,从而得:(DG+GF+EF+ED)的最小值=D′E′+DE,求出D′E′与DE的长即可得到答案.
(3)根据三角形的面积,首先求得点P到OD的距离,然后过点O作OF⊥OD,使OF等于点P到OD的距离,过点F作FG∥OD,求得FG的解析式,然后再求直线FG与抛物线交点的坐标即可得到点P的坐标.
【解答】解:(1)将A(0,4)、C(5,0)代入二次函数y=x2+bx+c,得
,
解得.
故二次函数的表达式y=x2﹣x+4;
(2)如图:
延长EC至E′,使E′C=EC,延长DA至D′,使D′A=DA,连接D′E′,交x轴于F点,交y轴于G点,
GD=GD′EF=E′F,
(DG+GF+EF+ED)最小=D′E′+DE,
由E点坐标为(5,2),BC的中点;D(4,4),直角的角平分线上的点;得D′(﹣4,4),E(5,﹣2).
由勾股定理,得
DE==,D′E′==,
(DG+GF+EF+ED)最小=D′E′+DE=+;
(3)如下图:
OD=.
∵S△ODP的面积=12,
∴点P到OD的距离==3.
过点O作OF⊥OD,取OF=3,过点F作直线FG∥OD,交抛物线与点P1,P2,
在Rt△OGF中,OG===6,
∴直线GF的解析式为y=x﹣6.
将y=x﹣6代入y=得:x﹣6=,
解得:,,
将x1、x2的值代入y=x﹣6得:y1=,y2=
∴点P1(,),P2(,)
如下图所示:
过点O作OF⊥OD,取OF=3,过点F作直线FG交抛物线与P3,P4,
在Rt△PFO中,OG==6
∴直线FG的解析式为y=x+6,
将y=x+6代入y=得:x+6=
解得:,
y1=x1+6=,y2=x2+6=
∴p3(,),p4(,)
综上所述:点P的坐标为:(,)或(,)或(,)或(,).
名校入学考试校考卷
一、选择题:(本大题12个小题,每小题4分,共48分)每个小题都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案的代号填入答题卡上对应位置中.
1.已知△ABC中,AC=4,BC=3,AB=5,则sinA=( )
A.
B.
C.
D.
2.用配方法解方程x2+4x﹣5=0,下列配方正确的是( )
A.(x+2)2=1
B.(x+2)2=5
C.(x+2)2=9
D.(x+4)2=9
3.下列式子,正确的是( )
A.3+=3
B.(
+1)(﹣1)=1
C.2﹣1=﹣2
D.x2+2xy﹣y2=(x﹣y)2
4.在?ABCD中,若∠A:∠B=1:2,则∠A的度数是( )
A.60°
B.90°
C.120°
D.150°
5.已知一个等腰三角形的两条边长分别为3和8,则这个等腰三角形的周长为( )
A.11
B.14
C.19
D.14或19
6.二次函数y=﹣2(x﹣4)2﹣5的开口方向、对称轴分别是( )
A.开口向上、直线x=﹣4
B.开口向上、直线x=4
C.开口向下、直线x=﹣4
D.开口向下、直线x=4
7.如图,在⊙O中,∠AOB=50°,则∠ACB=( )
A.30°
B.25°
C.50°
D.40°
8.如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )
A.30°
B.45°
C.55°
D.75°
9.某校九年级(1)班有7个合作学习小组,各学习小组的人数分别为:5,6,6,x,7,8,9,已知这组数据的平均数是7,则这组数据的中位数是( )
A.6
B.7
C.8
D.9
10.下列图形都是由几个黑色和白色的正方形按一定规律组成,图①中有2个黑色正方形,图②中有5个黑色正方形,图③中有8个黑色正方形,图④中有11个黑色正方形,…,依次规律,图⑩中黑色正方形的个数是
( )
A.32
B.29
C.28
D.26
11.如图,在平面直角坐标系中,将矩形OABC沿对角线OB对折,使点A(,0)落在点A1处,已知点B的坐标是(,1),则点A1的坐标是( )
A.(,)
B.(,)
C.(,2)
D.(,)
12.如图,在平面直角坐标系系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=在第一象限内的图象交于点B,连接B0.若S△OBC=1,tan∠BOC=,则k2的值是( )
A.﹣3
B.1
C.2
D.3
二.填空(本大题6个小题,每小题4分共24分)
13.方程(x﹣2)2=4的根是 .
14.计算:2cos60°﹣tan45°= .
15.已知一个菱形的两条对角线长分别为6cm和8cm,则这个菱形的面积为 cm2.
16.在某时刻的阳光照耀下,身高160cm的阿美的影长为80cm,她身旁的旗杆影长5m,则旗杆高为 m.
17.从﹣1,0,1,2,3这五个数中,随机抽取一个数记为m,则使关于x的不等式组有解,并且使函数y=(m﹣1)x2+2mx+m+2与x轴有交点的概率为 .
18.在?ABCD中,AB<BC,已知∠B=30°,AB=2,将△ABC沿AC翻折至△AB′C,使点B′落在?ABCD所在的平面内,连接B′D.若△AB′D是直角三角形,则BC的长为 .
三.解答题(本大题2小题,每小题7分,共14分)解答时每小题必须给出必要的演算过程或推理步骤.
19.解二元一次方程组.
20.为有效开展阳光体育活动,云洱中学利用课外活动时间进行班级篮球比赛,每场比赛都要决出胜负,每队胜一场得2分,负一场得1分.已知九年级一班在8场比赛中得到13分,问九年级一班胜、负场数分别是多少?
四、解答题:(本大题4个小题,每小题10分,共40分,解答题时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线).)
21.先化简,再求值:(﹣)÷,其中x=tan60°+2.
22.2015年1月,市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价.评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查,了解他们每天在课外用于学习的时间,并绘制成如下不完整的统计图.
根据上述信息,解答下列问题:
(1)本次抽取的学生人数是 ;扇形统计图中的圆心角α等于 ;补全统计直方图;
(2)被抽取的学生还要进行一次50米跑测试,每5人一组进行.在随机分组时,小红、小花两名女生被分到同一个小组,请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率.
23.“村村通公路”工程是国家为支持新农村建设的一项重大举措,为了落实这一举措,重庆潼南县政府计划在南北方向的A、B两村之间建一条公路AB.已知公路AB的一侧有C村,在公路AB上的M处测得C村在M的南偏东37°方向上,从M向南走270米到达N处,测得C村在N的东南方向上,且C村周围800米范围内为油菜花田,那么计划修建的公路AB是否会穿过油菜花田,请说明理由(参考数据:sin37°≈0.8,cos37°≈0.8,tan37°≈0.75)
24.长宽比为(n为正整数)的矩形称为矩形.下面,我们通过折叠的方式折出一个矩形,如图①所示.
操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.
操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.
则四边形BCEF为矩形.
证明:设正方形ABCD的边长为1,则BD=.
由折叠性质可知BG=BC=1,∠AFE=∠BFE=90°,则四边形BCEF为矩形.
∴∠A=∠BFE.∴EF∥AD.
∴,即,∴.∴.
∴四边形BCEF为矩形.
阅读以上内容,回答下列问题:
(1)在图①中,所有与CH相等的线段是 ,tan∠HBC的值是 ;
(2)已知四边形BCEF为矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN为矩形;
(3)将图②中的矩形BCMN沿用(2)中的方式操作3次后,得到一个“矩形”,则n的值是 .
五、解答题(本大题2个小题,每小题12分,共24分)解答时每小题都必须写出必要的演算过程或推理步骤,请将解答过程书写在答卷中对应的位置上.
25.已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE′,连接EE′.
(1)如图1,∠AEE′= °;
(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;
(3)如图3,在(2)的条件下,如果CE=2,AE=,求ME的长.
26.如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,∠AOC的平分线交AB于点D,E为BC的中点,已知A(0,4)、C(5,0),二次函数y=x2+bx+c的图象抛物线经过A,C两点.
(1)求该二次函数的表达式;
(2)F、G分别为x轴,y轴上的动点,顺次连接D、E、F、G构成四边形DEFG,求四边形DEFG周长的最小值;
(3)抛物线上是否在点P,使△ODP的面积为12?若存在,求出点P的坐标;若不存在,请说明理由.
2015-2016年九年级(下)入学考试数学试卷
参考答案与试题解析
一、选择题:(本大题12个小题,每小题4分,共48分)每个小题都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案的代号填入答题卡上对应位置中.
1.已知△ABC中,AC=4,BC=3,AB=5,则sinA=( )
A.
B.
C.
D.
【考点】锐角三角函数的定义;勾股定理的逆定理.
【分析】先根据直角三角形的三边长判断出三角形的形状,再根据锐角三角函数的定义求解即可.
【解答】解:∵△ABC中,AC=4,BC=3,AB=5,即42+32=52,
∴△ABC是直角三角形,∠C=90°.
sinA==.
故选A.
2.用配方法解方程x2+4x﹣5=0,下列配方正确的是( )
A.(x+2)2=1
B.(x+2)2=5
C.(x+2)2=9
D.(x+4)2=9
【考点】解一元二次方程-配方法.
【分析】先将原方程进行配方,然后选项进行对照,即可得到正确选项.
【解答】解:x2+4x﹣5=0,
配方,得
(x+2)2=9.
故选C.
3.下列式子,正确的是( )
A.3+=3
B.(
+1)(﹣1)=1
C.2﹣1=﹣2
D.x2+2xy﹣y2=(x﹣y)2
【考点】二次根式的乘除法;负整数指数幂.
【分析】根据二次根式的加减、负整数指数幂和完全平方公式判断.
【解答】解:A、不是同类二次根式,不能相加,故错误;
B、正确;
C、原式=,故错误;
D、与完全平方公式不符,故错误.
故选B.
4.在?ABCD中,若∠A:∠B=1:2,则∠A的度数是( )
A.60°
B.90°
C.120°
D.150°
【考点】平行四边形的性质.
【分析】根据平行四边形的基本性质可知,平行四边形的邻角互补,由已知可得,∠A、∠B是邻角,故∠A可求解.
【解答】解:∵?ABCD,
∴∠A+∠B=180°,
而∠A:∠B=1:2
∴∠A=60°,∠B=120°
∴∠A=60°.
故选A.
5.已知一个等腰三角形的两条边长分别为3和8,则这个等腰三角形的周长为( )
A.11
B.14
C.19
D.14或19
【考点】等腰三角形的性质;三角形三边关系.
【分析】分3是腰长与底边长两种情况讨论求解即可.
【解答】解:①3是腰长时,三角形的三边分别为3、3、8,
∵3+3=6<8,
∴此时不能组成三角形;
②3是底边长时,三角形的三边分别为3、8、8,
此时能组成三角形,
所以,周长=3+8+8=19,
综上所述,这个等腰三角形的周长是19.
故选C.
6.二次函数y=﹣2(x﹣4)2﹣5的开口方向、对称轴分别是( )
A.开口向上、直线x=﹣4
B.开口向上、直线x=4
C.开口向下、直线x=﹣4
D.开口向下、直线x=4
【考点】二次函数的性质.
【分析】已知抛物线解析式为顶点式,可根据顶点式求抛物线的开口方向,对称轴.
【解答】解:由y=﹣2(x﹣4)2﹣5可知,二次项系数为﹣2<0,
∴抛物线开口向下,对称轴为直线x=4,
故选D.
7.如图,在⊙O中,∠AOB=50°,则∠ACB=( )
A.30°
B.25°
C.50°
D.40°
【考点】圆周角定理.
【分析】直接根据圆周角定理求解即可.
【解答】解:∠ACB=∠AOB=×50°=25°.
故选:B.
8.如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )
A.30°
B.45°
C.55°
D.75°
【考点】线段垂直平分线的性质;等腰三角形的性质.
【分析】根据等腰三角形的性质得到∠A=∠ACB=75°,根据线段垂直平分线的性质得到BD=CD,求得∠DCE=∠B=30°,即可得到结论.
【解答】解:∵AB=BC,∠B=30°,
∴∠A=∠ACB=75°,
∵DE垂直平分BC,
∴BD=CD,
∴∠DCE=∠B=30°,
∴∠ACD=∠ACB=∠DCB=45°,
故选B.
9.某校九年级(1)班有7个合作学习小组,各学习小组的人数分别为:5,6,6,x,7,8,9,已知这组数据的平均数是7,则这组数据的中位数是( )
A.6
B.7
C.8
D.9
【考点】中位数;算术平均数.
【分析】根据题意首先求出x的值,再利用中位数的定义求出答案.
【解答】解:∵5,6,6,x,7,8,9,这组数据的平均数是7,
∴5+6+6+x+7+8+9=7×7,
解得:x=8,
故这组数据按从小到大排列:5,6,6,7,8,8,9,
则这组数据的中位数是:7.
故选:B.
10.下列图形都是由几个黑色和白色的正方形按一定规律组成,图①中有2个黑色正方形,图②中有5个黑色正方形,图③中有8个黑色正方形,图④中有11个黑色正方形,…,依次规律,图⑩中黑色正方形的个数是
( )
A.32
B.29
C.28
D.26
【考点】规律型:图形的变化类.
【分析】仔细观察图形,找到图形的个数与黑色正方形的个数的通项公式后代入n=11后即可求解.
【解答】解:观察图形发现:
图①中有2个黑色正方形,
图②中有2+3×(2﹣1)=5个黑色正方形,
图③中有2+3(3﹣1)=8个黑色正方形,
图④中有2+3(4﹣1)=11个黑色正方形,
…,
图n中有2+3(n﹣1)=3n﹣1个黑色的正方形,
当n=10时,2+3×(10﹣1)=29,
故选B.
11.如图,在平面直角坐标系中,将矩形OABC沿对角线OB对折,使点A(,0)落在点A1处,已知点B的坐标是(,1),则点A1的坐标是( )
A.(,)
B.(,)
C.(,2)
D.(,)
【考点】翻折变换(折叠问题);坐标与图形性质.
【分析】由已知可得∠AOB=30°,翻折后找到相等的角及相等的边,在直角三角形中,利用勾股定理可求得答案.
【解答】解:过A1作A1D⊥OA,
∵A(,0),B的坐标是(,1),
∴OA=,AB=1,
在Rt△OAB中,OB==2,AB=1,
∴AB=OB,
∵△AOB是直角三角形,
∴∠AOB=30°,
OB为折痕,
∴∠A1OB=∠AOB=30°,OA1=OA=,
Rt△OA1D中,∠OA1D=30°,
∴OD=×=,
A1D=×=,
∴点A1的坐标(,).
故选B.
12.如图,在平面直角坐标系系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=在第一象限内的图象交于点B,连接B0.若S△OBC=1,tan∠BOC=,则k2的值是( )
A.﹣3
B.1
C.2
D.3
【考点】反比例函数与一次函数的交点问题.
【分析】首先根据直线求得点C的坐标,然后根据△BOC的面积求得BD的长,然后利用正切函数的定义求得OD的长,从而求得点B的坐标,求得结论.
【解答】解:∵直线y=k1x+2与x轴交于点A,与y轴交于点C,
∴点C的坐标为(0,2),
∴OC=2,
∵S△OBC=1,
∴BD=1,
∵tan∠BOC=,
∴=,
∴OD=3,
∴点B的坐标为(1,3),
∵反比例函数y=在第一象限内的图象交于点B,
∴k2=1×3=3.
故选D.
二.填空(本大题6个小题,每小题4分共24分)
13.方程(x﹣2)2=4的根是 4,0 .
【考点】解一元二次方程-直接开平方法.
【分析】根据方程的特点,用直接开平方法解一元二次方程即可.
【解答】解:(x﹣2)2=4,
x﹣2=±2,
解得:x1=4,x2=0.
故答案为:4,0.
14.计算:2cos60°﹣tan45°= 0 .
【考点】特殊角的三角函数值.
【分析】将特殊角的三角函数值直接代入即可求解.
【解答】解:2cos60°﹣tan45°=2×﹣1=0.
15.已知一个菱形的两条对角线长分别为6cm和8cm,则这个菱形的面积为 24 cm2.
【考点】菱形的性质.
【分析】根据菱形的面积等于两对角线乘积的一半求得其面积即可.
【解答】解:∵一个菱形的两条对角线长分别为6cm和8cm,
∴这个菱形的面积=×6×8=24(cm2).
故答案为:24.
16.在某时刻的阳光照耀下,身高160cm的阿美的影长为80cm,她身旁的旗杆影长5m,则旗杆高为 10 m.
【考点】相似三角形的应用.
【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.
【解答】解:根据相同时刻的物高与影长成比例,设旗杆的高度为x
m,则
160:80=x:5,
解得x=10.
故答案是:10.
17.从﹣1,0,1,2,3这五个数中,随机抽取一个数记为m,则使关于x的不等式组有解,并且使函数y=(m﹣1)x2+2mx+m+2与x轴有交点的概率为 .
【考点】概率公式;解一元一次不等式组;抛物线与x轴的交点.
【分析】首先解不等式以及利用二次函数与x轴交点个数和△的关系分别得出m的取值范围,进而利用概率公式求出即可.
【解答】解:∵x+1≤m,解得;x≤m﹣1,
2﹣x≤2m,解得:x≥2﹣2m,
∴使关于x的不等式组有解,则m﹣1≥2﹣2m,
解得:m≥1,
∵使函数y=(m﹣1)x2+2mx+m+2与x轴有交点,
∴b2﹣4ac4m2﹣4(m﹣1)(m+2)=﹣4m+8≥0,
解得:m≤2,
∴m的取值范围是:1≤m≤2,
∴从﹣1,0,1,2,3这五个数中,随机抽取一个数记为m,符合题意的有1,2,
故使关于x的不等式组有解,并且使函数y=(m﹣1)x2+2mx+m+2与x轴有交点的概率为.
故答案为:.
18.在?ABCD中,AB<BC,已知∠B=30°,AB=2,将△ABC沿AC翻折至△AB′C,使点B′落在?ABCD所在的平面内,连接B′D.若△AB′D是直角三角形,则BC的长为 4或6 .
【考点】翻折变换(折叠问题);平行四边形的性质.
【分析】在?ABCD中,AB<BC,要使△AB′D是直角三角形,有两种情况:∠B′AD=90°或∠AB′D=90°,画出图形,分类讨论即可.
【解答】解:当∠B′AD=90°AB<BC时,如图1,
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AD∥BC,∠B′AD=90°,
∴∠B′GC=90°,
∵∠B=30°,AB=2,
∴∠AB′C=30°,
∴GC=
B′C=
BC,
∴G是BC的中点,
在Rt△ABG中,BG=AB=×2=3,
∴BC=6;
当∠AB′D=90°时,如图2,
∵AD=BC,BC=B′C,
∴AD=B′C,
∵由折叠的性质:∠BAC=90°,
∴AC∥B′D,
∴四边形ACDB′是等腰梯形,
∵∠AB′D=90°,
∴四边形ACDB′是矩形,
∴∠BAC=90°,
∵∠B=30°,AB=2,
∴BC=AB÷=2×=4,
∴当BC的长为4或6时,△AB′D是直角三角形.
故答案为:4或6.
三.解答题(本大题2小题,每小题7分,共14分)解答时每小题必须给出必要的演算过程或推理步骤.
19.解二元一次方程组.
【考点】解二元一次方程组.
【分析】方程组利用加减消元法求出解即可.
【解答】解:②﹣①得:5y=5,即y=1,
把y=1代入①得:x=3,
则方程组的解为.
20.为有效开展阳光体育活动,云洱中学利用课外活动时间进行班级篮球比赛,每场比赛都要决出胜负,每队胜一场得2分,负一场得1分.已知九年级一班在8场比赛中得到13分,问九年级一班胜、负场数分别是多少?
【考点】一元一次方程的应用.
【分析】设胜了x场,那么负了(8﹣x)场,根据得分为13分可列方程求解.
【解答】解:设胜了x场,那么负了(8﹣x)场,根据题意得:
2x+1?(8﹣x)=13,
x=5,
8﹣5=3.
答:九年级一班胜、负场数分别是5和3.
四、解答题:(本大题4个小题,每小题10分,共40分,解答题时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线).)
21.先化简,再求值:(﹣)÷,其中x=tan60°+2.
【考点】分式的化简求值;特殊角的三角函数值.
【分析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
【解答】解:原式=[﹣]?=?=?=,
当x=tan60°+2=+2时,原式=.
22.2015年1月,市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价.评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查,了解他们每天在课外用于学习的时间,并绘制成如下不完整的统计图.
根据上述信息,解答下列问题:
(1)本次抽取的学生人数是 30 ;扇形统计图中的圆心角α等于 144° ;补全统计直方图;
(2)被抽取的学生还要进行一次50米跑测试,每5人一组进行.在随机分组时,小红、小花两名女生被分到同一个小组,请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率.
【考点】列表法与树状图法;扇形统计图;利用频率估计概率.
【分析】(1)根据题意列式求值,根据相应数据画图即可;
(2)根据题意列表,然后根据表中数据求出概率即可.
【解答】解:(1)6÷20%=30,(30﹣3﹣7﹣6﹣2)÷30×360=12÷30×26=144°,
答:本次抽取的学生人数是30人;扇形统计图中的圆心角α等于144°;
故答案为:30,144°;
补全统计图如图所示:
(2)根据题意列表如下:
设竖列为小红抽取的跑道,横排为小花抽取的跑道,
小红
小花
1
2
3
4
5
1
(2,1)
(3,1)
(4,1)
(5,1)
2
(1,2)
(3,2)
(4,2)
(5,2)
3
(1,3)
(2,3)
(4,3)
(5,3)
4
(1,4)
(2,4)
(3,4)
(5,4)
5
(1,5)
(2,5)
(3,5)
(4,5)
记小红和小花抽在相邻两道这个事件为A,
∴.
23.“村村通公路”工程是国家为支持新农村建设的一项重大举措,为了落实这一举措,重庆潼南县政府计划在南北方向的A、B两村之间建一条公路AB.已知公路AB的一侧有C村,在公路AB上的M处测得C村在M的南偏东37°方向上,从M向南走270米到达N处,测得C村在N的东南方向上,且C村周围800米范围内为油菜花田,那么计划修建的公路AB是否会穿过油菜花田,请说明理由(参考数据:sin37°≈0.8,cos37°≈0.8,tan37°≈0.75)
【考点】解直角三角形的应用-方向角问题.
【分析】本题要求的实际上是C到AB的距离,过C点作CD⊥AB,CD就是所求的线段,由于CD是条公共直角边,可用CD表示出MD,ND,然后根据MN的长,来求出CD的长.
【解答】解:如图,过C点作CD⊥AB于D,
由题可知:∠CND=45°,∠CMD=37°.
设CD=x千米,tan∠CMD=,
则MD=.
tan∠CND=,
则ND==x,
∵MN=270米,
∴MD﹣ND=MN,即tan37°x﹣x=270,
∴﹣x=270,
解得
x=810.
∵810米>800米,
∴计划修建的公路AB是不会穿过油菜花田.
答:计划修建的公路AB是不会穿过油菜花田.
24.长宽比为(n为正整数)的矩形称为矩形.下面,我们通过折叠的方式折出一个矩形,如图①所示.
操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.
操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.
则四边形BCEF为矩形.
证明:设正方形ABCD的边长为1,则BD=.
由折叠性质可知BG=BC=1,∠AFE=∠BFE=90°,则四边形BCEF为矩形.
∴∠A=∠BFE.∴EF∥AD.
∴,即,∴.∴.
∴四边形BCEF为矩形.
阅读以上内容,回答下列问题:
(1)在图①中,所有与CH相等的线段是 GH、DG ,tan∠HBC的值是 ﹣1 ;
(2)已知四边形BCEF为矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN为矩形;
(3)将图②中的矩形BCMN沿用(2)中的方式操作3次后,得到一个“矩形”,则n的值是 6 .
【考点】几何变换综合题.
【分析】(1)设CH=GH=DG=x,根据DC=DH+CH=1,列出方程即可求出HC,然后运用三角函数的定义求出tan∠HBC的值.
(2)只需借鉴阅读中证明“四边形BCEF为矩形”的方法就可解决问题.
(3)利用(2)中结论,寻找规律可得到n的值.
【解答】解:(1)如图①中,由折叠可得:
DG=HG,GH=CH,
∴DG=GH=CH.
设HC=x,则DG=GH=x.
∵∠DGH=90°,
∴DH=x,
∴DC=DH+CH=x+x=1,
解得x=﹣1.
∴tan∠HBC===﹣1.
故答案为:GH、DG,;
(2)如图②中,∵BC=1,EC=BF=,
∴BE==
由折叠可得BP=BC=1,∠FNM=∠BNM=90°,∠EMN=∠CMN=90°.
∵四边形BCEF是矩形,
∴∠F=∠FEC=∠C=∠FBC=90°,
∴四边形BCMN是矩形,∠BNM=∠F=90°,
∴MN∥EF,
∴=,
即BP?BF=BE?BN,
∴1×=BN,
∴BN=,
∴BC:BN=1:
=:1,
∴四边形BCMN是的矩形;
(3)同理可得:
将矩形沿用(2)中的方式操作1次后,得到一个“矩形”,
将矩形沿用(2)中的方式操作1次后,得到一个“矩形”,
将矩形沿用(2)中的方式操作1次后,得到一个“矩形”,
所以将图②中的矩形BCMN沿用(2)中的方式操作3次后,得到一个“矩形”.
故答案为6.
五、解答题(本大题2个小题,每小题12分,共24分)解答时每小题都必须写出必要的演算过程或推理步骤,请将解答过程书写在答卷中对应的位置上.
25.已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE′,连接EE′.
(1)如图1,∠AEE′= 30 °;
(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;
(3)如图3,在(2)的条件下,如果CE=2,AE=,求ME的长.
【考点】几何变换综合题.
【分析】(1)根据旋转性质以及三角形内角和定理即可解决.
(2)根据EM∥FE′可以得==,再根据AN=NE,BE′=DE即可得到线段DE、BF、ME之间的关系.
(3)通过辅助线求出线段E′F=7,E′Q=9,再由(2)的结论得到ME的长.
【解答】解:(1)∵△ABE′是由△ADE绕点A顺时针旋转120°得到,
∴∠EAE′=120°,AE=AE′,
∴∠E′=∠AEE′==30°,
故答案为30°.
(2)①当点E在CD上时,DE+BF=2ME,理由如下:
如图1,当点E在线段CD上,AF交EE′于N,
∵∠EAF=30°,∠EAE′=120,
∴∠E′AN=90°,
∴E′N=2AN,
∵∠NAE=∠NEA=30°,
∴NA=NE,E′N=2EN,
∵EM∥FE′,
∴==,
∵BE′=DE,
∴E′F=2ME,
∴DE+BF=2ME.
②当点E在CD延长线上,0°<∠EAD∠30°时,BF﹣DE=2ME,理由如下:
如图2,∵∠EAF=30°,∠EAE′=120,
∴∠E′AN=90°,
∴E′N=2AN,
∵∠NAE=∠NEA=30°,
∴NA=NE,E′N=2EN,
∵EM∥FE′,
∴==,
∵BE′=DE,
∴E′F=2ME,
∴BF﹣DE=2ME.
③当30°<∠EAD∠90°时,DE+BF=2ME,理由如下:
如图3,∵∠EAM=30°,∠EAE′=120,
∴∠E′AN=90°,
∴E′N=2AN,
∵∠NAE=∠NEA=30°,
∴NA=NE,E′N=2EN,
∵EM∥FE′,
∴==,
∵BE′=DE,
∴E′F=2ME,
∴BF+DE=2ME.
④当90°<∠EAD<120°时,DE﹣BF=2ME,理由如下:
如图4,∵∠EAM=30°,∠EAE′=120,
∴∠E′AN=90°,
∴E′N=2AN,
∵∠NAE=∠NEA=30°,
∴NA=NE,E′N=2EN,
∵EM∥FE′,
∴==,
∵BE′=DE,
∴E′F=2ME,
∴DE﹣BF=2ME.
(3)如图5,作AG⊥BC于点G,DH⊥BC于H,AP⊥EE′于P,EQ⊥BC于Q,
∵AD∥BC,AD=AB=CD,∠BAD=120°,易知四边形AGHD是矩形,
在△AGB和△DHC中,
,
∴△AGB≌△DHC,
∴BG=HC,AD=GH,
∵∠ABE′=∠ADC=120°,
∴点E′、B、C共线,设AD=AB=CD=x,则GH=x,BG=CH=x,
在RT△EQC中,CE=2,∠ECQ=60°,
∴CQ=EC=1,EQ=,
∴E′Q=BC+BE′﹣CQ=3x﹣3,
在RT△APE中,AE=2,∠AEP=30°,
∴AP=,PE=,
∵AE=AE′,AP⊥EE′,
∴PE=PE′=,
∴EE′=2,
在RT△E′EQ中,E′Q==9,
∴3x﹣3=9,
∴x=4,
∴DE=BE′=2,BC=8,BG=2,
∴E′G=4,
∵∠AE′G=′AE′F,∠AGE′=∠FAE′,
∴△AGE′∽△FAE′,
∴,
∴,
∴E′F=7,
∴BF=E′F﹣E′B=7﹣2=5,
∵DE+BF=2ME
∴ME=.
26.如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,∠AOC的平分线交AB于点D,E为BC的中点,已知A(0,4)、C(5,0),二次函数y=x2+bx+c的图象抛物线经过A,C两点.
(1)求该二次函数的表达式;
(2)F、G分别为x轴,y轴上的动点,顺次连接D、E、F、G构成四边形DEFG,求四边形DEFG周长的最小值;
(3)抛物线上是否在点P,使△ODP的面积为12?若存在,求出点P的坐标;若不存在,请说明理由.
【考点】二次函数综合题.
【分析】(1)根据待定系数法,可得函数解析式;
(2)延长EC至E′,使E′C=EC,延长DA至D′,使D′A=DA,连接D′E′,交x轴于F点,交y轴于G点,则有:GD=GD′,EF=E′F,从而得:(DG+GF+EF+ED)的最小值=D′E′+DE,求出D′E′与DE的长即可得到答案.
(3)根据三角形的面积,首先求得点P到OD的距离,然后过点O作OF⊥OD,使OF等于点P到OD的距离,过点F作FG∥OD,求得FG的解析式,然后再求直线FG与抛物线交点的坐标即可得到点P的坐标.
【解答】解:(1)将A(0,4)、C(5,0)代入二次函数y=x2+bx+c,得
,
解得.
故二次函数的表达式y=x2﹣x+4;
(2)如图:
延长EC至E′,使E′C=EC,延长DA至D′,使D′A=DA,连接D′E′,交x轴于F点,交y轴于G点,
GD=GD′EF=E′F,
(DG+GF+EF+ED)最小=D′E′+DE,
由E点坐标为(5,2),BC的中点;D(4,4),直角的角平分线上的点;得D′(﹣4,4),E(5,﹣2).
由勾股定理,得
DE==,D′E′==,
(DG+GF+EF+ED)最小=D′E′+DE=+;
(3)如下图:
OD=.
∵S△ODP的面积=12,
∴点P到OD的距离==3.
过点O作OF⊥OD,取OF=3,过点F作直线FG∥OD,交抛物线与点P1,P2,
在Rt△OGF中,OG===6,
∴直线GF的解析式为y=x﹣6.
将y=x﹣6代入y=得:x﹣6=,
解得:,,
将x1、x2的值代入y=x﹣6得:y1=,y2=
∴点P1(,),P2(,)
如下图所示:
过点O作OF⊥OD,取OF=3,过点F作直线FG交抛物线与P3,P4,
在Rt△PFO中,OG==6
∴直线FG的解析式为y=x+6,
将y=x+6代入y=得:x+6=
解得:,
y1=x1+6=,y2=x2+6=
∴p3(,),p4(,)
综上所述:点P的坐标为:(,)或(,)或(,)或(,).
同课章节目录
