北师大版八年级下册数学 1.2 直角三角形 同步练习(含答案)
文档属性
| 名称 | 北师大版八年级下册数学 1.2 直角三角形 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-02 00:00:00 | ||
图片预览

文档简介
1.2
直角三角形
同步练习
一、选择题:
1.
两个直角三角形全等的条件是(
)
A.一锐角对应相等?;
B.两锐角对应相等;
C.一条边对应相等;
?D.两条边对应相等
2.
如图,∠B=∠D=90°,BC=CD,∠1=30°,则∠2的度数为(
)
A.
30°
B.
60°
C.
30°和60°之间
D.
以上都不对
3.
如果两个直角三角形的两条直角边对应相等,那么两个直角三角形全等的
依据是(
)
?
A.
AAS?
B.SAS?
C.HL?
D.SSS
?4.
已知在△ABC和△DEF中,∠A=∠D=90°,则下列条件中不能判定△ABC和
△DEF全等的是(
)
A.AB=DE,AC=DF?
B.AC=EF,BC=DF
?
C.AB=DE,BC=EF?
D.∠C=∠F,BC=EF
?5.
如图,AB∥EF∥DC,∠ABC=90°,AB=DC,那么图中有全等三角形(
)
?
A.5对;
B.4对;
C.3对;
D.2对
?6.
要判定两个直角三角形全等,下列说法正确的有(?
)
?
①有两条直角边对应相等;
②有两个锐角对应相等;
③有斜边和一条直角边对应相等;
④有一条直角边和一个锐角相等;
⑤有斜边和一个锐角对应相等;
⑥有两条边相等.
?
A.6个?
B.5个?
C.4个?
D.3个
?
第2题图
第5题图
第7题图
第8题图
7.
如图,已知那么添加下列一个条件后,仍无法判定的是(
)
A. B.
C.
D.
8.
如图,已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是( )
A.
AB=AC
B.
∠BAC=90°
C.
BD=AC
D.
∠B=45°
二、填空题:
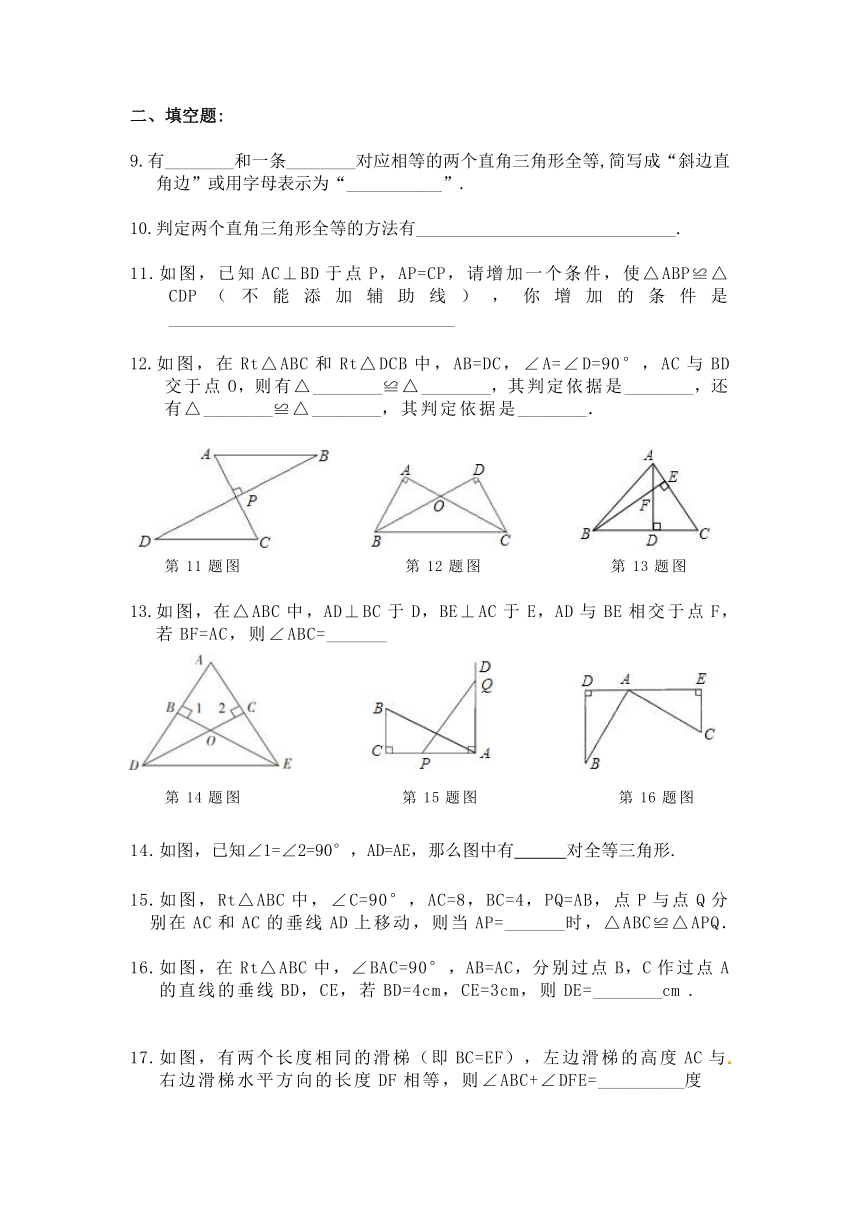
9.有________和一条________对应相等的两个直角三角形全等,简写成“斜边直角边”或用字母表示为“___________”.
10.判定两个直角三角形全等的方法有______________________________.
11.如图,已知AC⊥BD于点P,AP=CP,请增加一个条件,使△ABP≌△CDP(不能添加辅助线),你增加的条件是_________________________________
12.如图,在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△________≌△________,其判定依据是________,还有△________≌△________,其判定依据是________.
第11题图
第12题图
第13题图
13.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC=_______
第14题图
第15题图
第16题图
14.如图,已知∠1=∠2=90°,AD=AE,那么图中有
对全等三角形.
15.如图,Rt△ABC中,∠C=90°,AC=8,BC=4,PQ=AB,点P与点Q分别在AC和AC的垂线AD上移动,则当AP=_______时,△ABC≌△APQ.
16.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE=________cm
.
17.如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=__________度
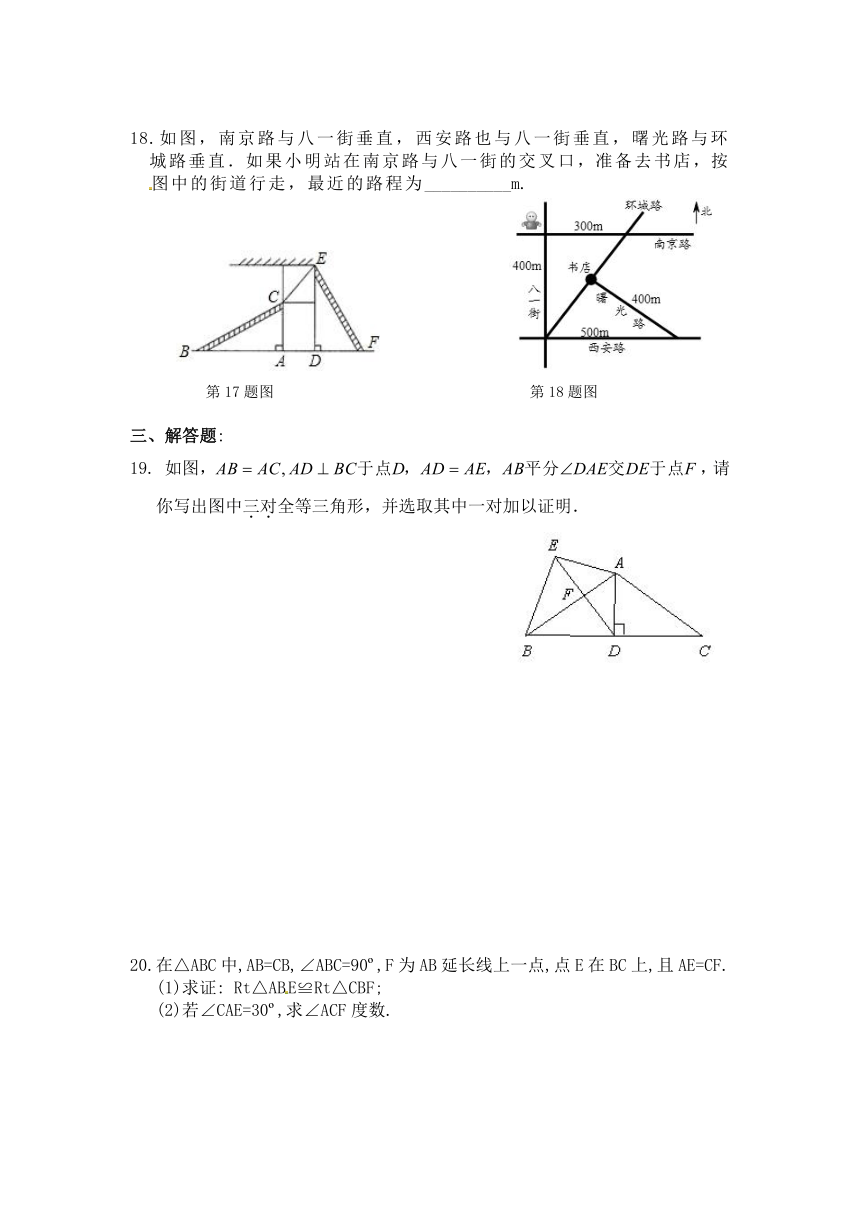
18.如图,南京路与八一街垂直,西安路也与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程为__________m.
第17题图
第18题图
三、解答题:
19.
如图,,请你写出图中三对全等三角形,并选取其中一对加以证明.
20.在△ABC中,AB=CB,∠ABC=90?,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:
Rt△ABE≌Rt△CBF;
(2)若∠CAE=30?,求∠ACF度数.
21.
如图
AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
?
?22.
已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.
??23.
如图,在△ABC中,以AB、AC为直角边,
分别向外作等腰直角三角形ABE、ACF,连结EF,过点A作AD⊥BC,垂足为D,反向延长DA交EF于点M.
?
(1)用圆规比较EM与FM的大小.
?
(2)你能说明由(1)中所得结论的道理吗?
?
参考答案
一、选择题
1.D
2.B
3.B
4.B
5.C
6.C
7.C
8.A
二、填空题
9.
斜边,直角边,HL
10.
SSS、ASA、AAS、SAS、HL
11.
BP=DP或AB=CD或∠A=∠C或∠B=∠D.
12.ABC,DCB,HL,AOB,DOC,AAS.
`13.
45°
14.
3
15.
4或8
16.
7
17.
90°
18.
500
三、解答题
19.解:(1)、、、、
(写出其中的三对即可).
(2)以为例证明.
证明:
在Rt和Rt中,
Rt≌Rt.
20.解:(1)∵∠ABC=90°,∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中,
∵AE=CF,
AB=BC,
∴Rt△ABE≌Rt△CBF(HL)
(2)
∵AB=BC,
∠ABC=90°,
∴
∠CAB=∠ACB=45°.
∵∠BAE=∠CAB-∠CAE=45°-30°=15°.
由(1)知
Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°,
∴∠ACF=∠BCF+∠ACB=45°+15°=60°.
21.(1)证明:在△ACD与△ABE中,
∵∠A=∠A,∠ADC=∠AEB=90°,AB=AC,
∴△ACD≌△ABE,
∴AD=AE.
(2)互相垂直,
在Rt△ADO与△AEO中,
∵OA=OA,AD=AE,
∴△ADO≌△AEO,
∴∠DAO=∠EAO,
即OA是∠BAC的平分线,
又∵AB=AC,
∴OA⊥BC.
?22.证明:∵BD⊥AE于D,CE⊥AE于E
?∴∠ADB=∠AEC=90°
?∵∠BAC=90°
?∴∠ABD+∠BAD=∠CAE+∠BAD
?∴∠ABD=∠CAE
?在△ABD和△CAE中
?∴△ABD≌△CAE(AAS)
?∴BD=AE,AD=CE
?∵AE=AD+DE
?∴BD=CE+DE
?
?23.
解:(1)EM=FM
?(2)作EH⊥AM,垂足为H,FK⊥AM,垂足为K
?先说明Rt△EHA≌Rt△ADB
得EH=AD
?Rt△FKA≌Rt△ADC
得FK=AD
得EH=FK
?在Rt△EHK与Rt△FKM中,Rt△EHM≌Rt△FKM
?得EM=FM.
直角三角形
同步练习
一、选择题:
1.
两个直角三角形全等的条件是(
)
A.一锐角对应相等?;
B.两锐角对应相等;
C.一条边对应相等;
?D.两条边对应相等
2.
如图,∠B=∠D=90°,BC=CD,∠1=30°,则∠2的度数为(
)
A.
30°
B.
60°
C.
30°和60°之间
D.
以上都不对
3.
如果两个直角三角形的两条直角边对应相等,那么两个直角三角形全等的
依据是(
)
?
A.
AAS?
B.SAS?
C.HL?
D.SSS
?4.
已知在△ABC和△DEF中,∠A=∠D=90°,则下列条件中不能判定△ABC和
△DEF全等的是(
)
A.AB=DE,AC=DF?
B.AC=EF,BC=DF
?
C.AB=DE,BC=EF?
D.∠C=∠F,BC=EF
?5.
如图,AB∥EF∥DC,∠ABC=90°,AB=DC,那么图中有全等三角形(
)
?
A.5对;
B.4对;
C.3对;
D.2对
?6.
要判定两个直角三角形全等,下列说法正确的有(?
)
?
①有两条直角边对应相等;
②有两个锐角对应相等;
③有斜边和一条直角边对应相等;
④有一条直角边和一个锐角相等;
⑤有斜边和一个锐角对应相等;
⑥有两条边相等.
?
A.6个?
B.5个?
C.4个?
D.3个
?
第2题图
第5题图
第7题图
第8题图
7.
如图,已知那么添加下列一个条件后,仍无法判定的是(
)
A. B.
C.
D.
8.
如图,已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是( )
A.
AB=AC
B.
∠BAC=90°
C.
BD=AC
D.
∠B=45°
二、填空题:
9.有________和一条________对应相等的两个直角三角形全等,简写成“斜边直角边”或用字母表示为“___________”.
10.判定两个直角三角形全等的方法有______________________________.
11.如图,已知AC⊥BD于点P,AP=CP,请增加一个条件,使△ABP≌△CDP(不能添加辅助线),你增加的条件是_________________________________
12.如图,在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△________≌△________,其判定依据是________,还有△________≌△________,其判定依据是________.
第11题图
第12题图
第13题图
13.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC=_______
第14题图
第15题图
第16题图
14.如图,已知∠1=∠2=90°,AD=AE,那么图中有
对全等三角形.
15.如图,Rt△ABC中,∠C=90°,AC=8,BC=4,PQ=AB,点P与点Q分别在AC和AC的垂线AD上移动,则当AP=_______时,△ABC≌△APQ.
16.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE=________cm
.
17.如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=__________度
18.如图,南京路与八一街垂直,西安路也与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程为__________m.
第17题图
第18题图
三、解答题:
19.
如图,,请你写出图中三对全等三角形,并选取其中一对加以证明.
20.在△ABC中,AB=CB,∠ABC=90?,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:
Rt△ABE≌Rt△CBF;
(2)若∠CAE=30?,求∠ACF度数.
21.
如图
AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
?
?22.
已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.
??23.
如图,在△ABC中,以AB、AC为直角边,
分别向外作等腰直角三角形ABE、ACF,连结EF,过点A作AD⊥BC,垂足为D,反向延长DA交EF于点M.
?
(1)用圆规比较EM与FM的大小.
?
(2)你能说明由(1)中所得结论的道理吗?
?
参考答案
一、选择题
1.D
2.B
3.B
4.B
5.C
6.C
7.C
8.A
二、填空题
9.
斜边,直角边,HL
10.
SSS、ASA、AAS、SAS、HL
11.
BP=DP或AB=CD或∠A=∠C或∠B=∠D.
12.ABC,DCB,HL,AOB,DOC,AAS.
`13.
45°
14.
3
15.
4或8
16.
7
17.
90°
18.
500
三、解答题
19.解:(1)、、、、
(写出其中的三对即可).
(2)以为例证明.
证明:
在Rt和Rt中,
Rt≌Rt.
20.解:(1)∵∠ABC=90°,∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中,
∵AE=CF,
AB=BC,
∴Rt△ABE≌Rt△CBF(HL)
(2)
∵AB=BC,
∠ABC=90°,
∴
∠CAB=∠ACB=45°.
∵∠BAE=∠CAB-∠CAE=45°-30°=15°.
由(1)知
Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°,
∴∠ACF=∠BCF+∠ACB=45°+15°=60°.
21.(1)证明:在△ACD与△ABE中,
∵∠A=∠A,∠ADC=∠AEB=90°,AB=AC,
∴△ACD≌△ABE,
∴AD=AE.
(2)互相垂直,
在Rt△ADO与△AEO中,
∵OA=OA,AD=AE,
∴△ADO≌△AEO,
∴∠DAO=∠EAO,
即OA是∠BAC的平分线,
又∵AB=AC,
∴OA⊥BC.
?22.证明:∵BD⊥AE于D,CE⊥AE于E
?∴∠ADB=∠AEC=90°
?∵∠BAC=90°
?∴∠ABD+∠BAD=∠CAE+∠BAD
?∴∠ABD=∠CAE
?在△ABD和△CAE中
?∴△ABD≌△CAE(AAS)
?∴BD=AE,AD=CE
?∵AE=AD+DE
?∴BD=CE+DE
?
?23.
解:(1)EM=FM
?(2)作EH⊥AM,垂足为H,FK⊥AM,垂足为K
?先说明Rt△EHA≌Rt△ADB
得EH=AD
?Rt△FKA≌Rt△ADC
得FK=AD
得EH=FK
?在Rt△EHK与Rt△FKM中,Rt△EHM≌Rt△FKM
?得EM=FM.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
