湘教版九年级数学上册 第3章图形的相似达标测试卷(含答案)
文档属性
| 名称 | 湘教版九年级数学上册 第3章图形的相似达标测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 435.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-02 10:38:25 | ||
图片预览



文档简介
第3章达标测试卷
一、选择题(每题3分,共30分)
1.若△ABC∽△A′B′C′,∠A=40°,∠B=60°,则∠C′等于( )
A.20°
B.40°
C.60°
D.80°
2.如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若=,则等于( )
A.
B.
C.
D.1
3.下列四组线段中,不是成比例线段的为( )
A.3,6,2,4
B.4,6,5,10
C.1,,,
D.2,,2
,
4.下列各组图形中有可能不相似的是( )
A.各有一个角是45°的两个等腰三角形
B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形
D.两个等腰直角三角形
5.如图,在平面直角坐标系中,有点A(6,3),B(6,0),以原点O为位似中心,位似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1)
B.(2,0)
C.(3,3)
D.(3,1)
6.下列说法:①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三角形斜边上的中线与斜边的比为1:2;④两个相似多边形的面积比为4:9,则周长的比为16:81.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
7.如图,为计算河的宽度(河两岸平行),在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一直线上,若测得BE=20
m,CE=10
m,CD=20
m,则河的宽度AB为( )
A.60
m
B.40
m
C.30
m
D.20
m
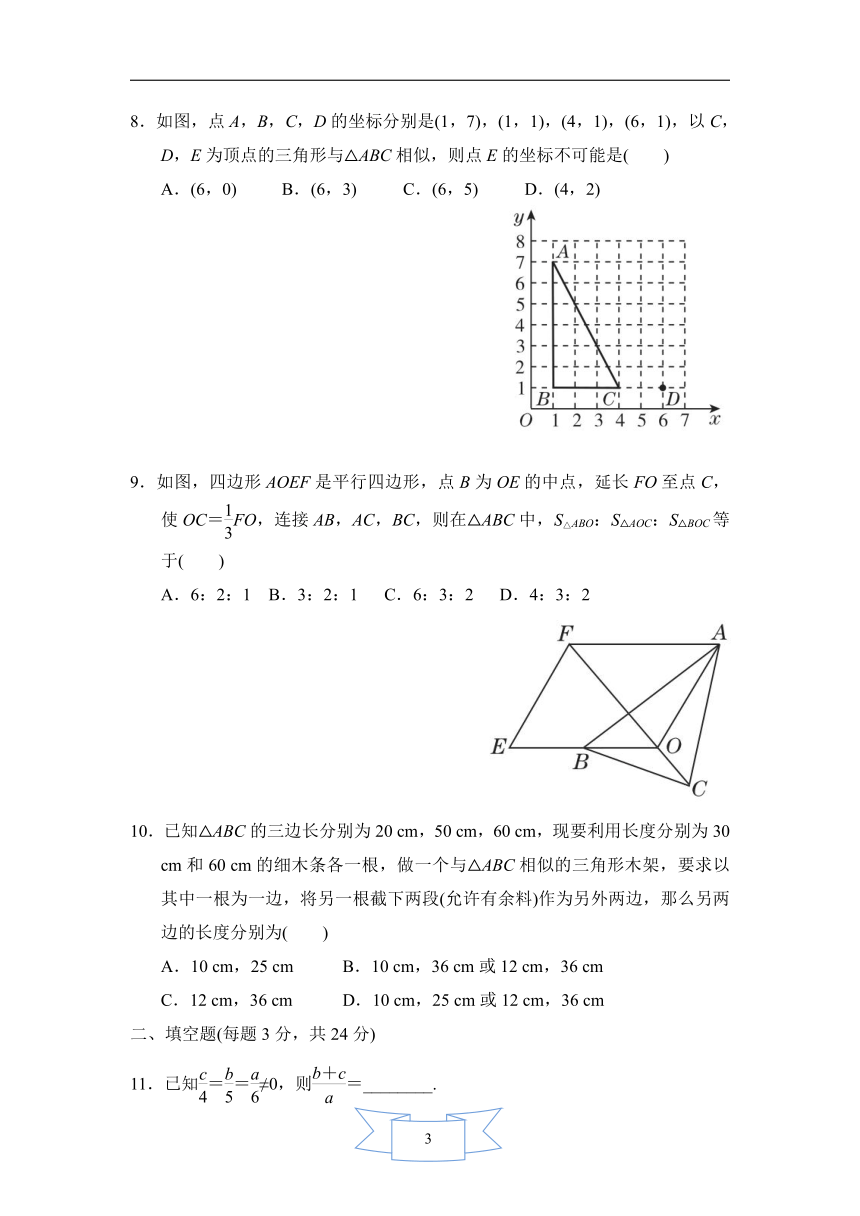
8.如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(6,0)
B.(6,3)
C.(6,5)
D.(4,2)
9.如图,四边形AOEF是平行四边形,点B为OE的中点,延长FO至点C,使OC=FO,连接AB,AC,BC,则在△ABC中,S△ABO:S△AOC:S△BOC等于( )
A.6:2:1
B.3:2:1
C.6:3:2
D.4:3:2
10.已知△ABC的三边长分别为20
cm,50
cm,60
cm,现要利用长度分别为30
cm和60
cm的细木条各一根,做一个与△ABC相似的三角形木架,要求以其中一根为一边,将另一根截下两段(允许有余料)作为另外两边,那么另两边的长度分别为( )
A.10
cm,25
cm
B.10
cm,36
cm或12
cm,36
cm
C.12
cm,36
cm
D.10
cm,25
cm或12
cm,36
cm
二、填空题(每题3分,共24分)
11.已知==≠0,则=________.
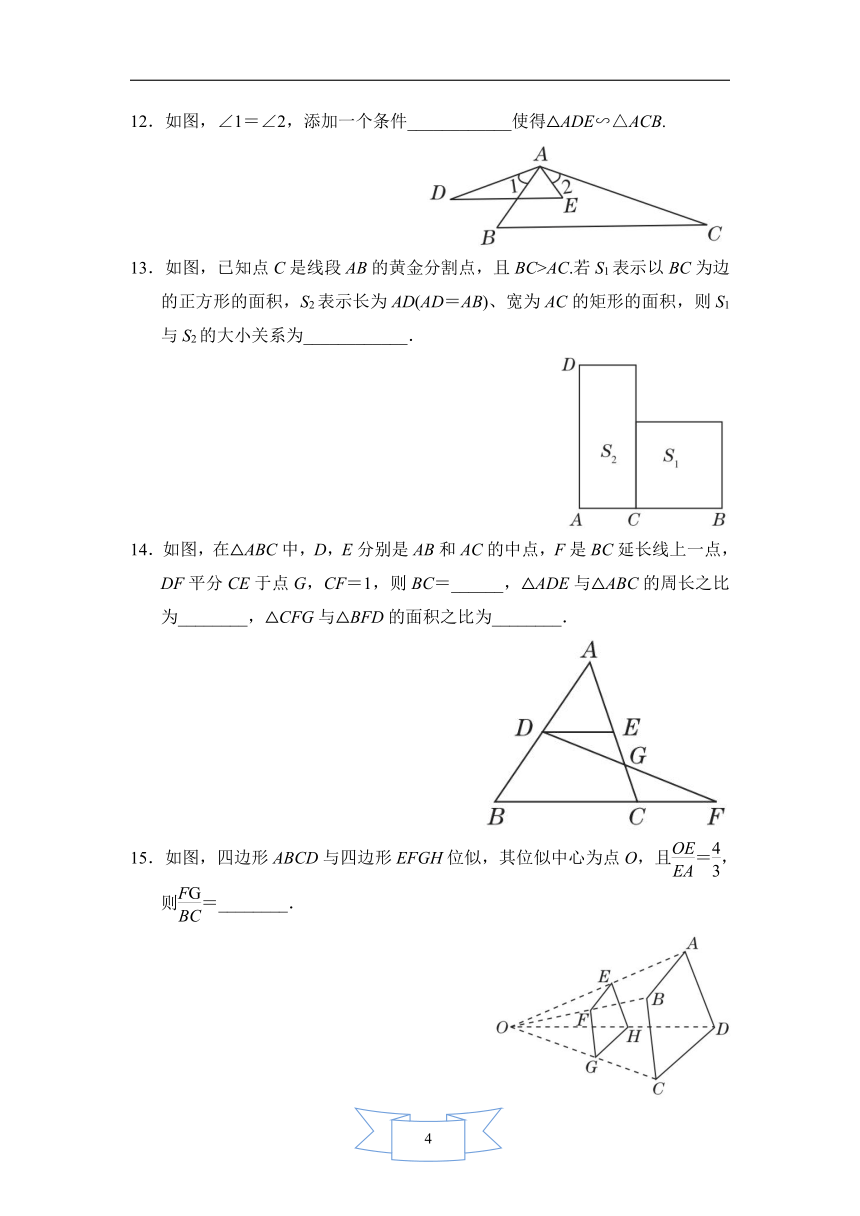
12.如图,∠1=∠2,添加一个条件____________使得△ADE∽△ACB.
13.如图,已知点C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形的面积,S2表示长为AD(AD=AB)、宽为AC的矩形的面积,则S1与S2的大小关系为____________.
14.如图,在△ABC中,D,E分别是AB和AC的中点,F是BC延长线上一点,DF平分CE于点G,CF=1,则BC=______,△ADE与△ABC的周长之比为________,△CFG与△BFD的面积之比为________.
15.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且=,则=________.
16.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形(如图),勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是________步.
17.矩形ABCD中,AB=6,BC=8,点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为____________.
18.如图,正三角形ABC的边长为2,以BC边上的高AB1为边作正三角形AB1C1,△ABC与△AB1C1公共部分的面积记为S1,再以正三角形AB1C1的边B1C1上的高AB2为边作正三角形AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2,……,以此类推,则Sn=______________(用含n的式子表示,n为正整数).
三、解答题(19~22题每题10分,23题12分,24题14分,共66分)
19.如图,四边形ABCD∽四边形EFGH,试求出x及∠α的大小.
20.如图,△ABC三个顶点的坐标分别为A(1,2),B(3,1),C(2,3),以原点O为位似中心,将△ABC放大为原来的2倍得△A′B′C′.
(1)在图中第一象限内画出符合要求的△A′B′C′(不要求写画法);
(2)计算△A′B′C′的面积.
21.如图,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.
(1)求证:△BDE∽△CAD;
(2)若AB=13,BC=10,求线段DE的长.
22.如图,竖立在B处的标杆AB=2.4米,在F处的观测者从E处看到标杆顶端A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8米,FB=2.5米,EF=1.5米,求树高CD.
23.如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上的某一点D处,折痕为EF(点E,F分别在边AC,BC上).
(1)若△CEF与△ABC相似.
①当AC=BC=2时,AD的长为________.
②当AC=3,BC=4时,AD的长为__________.
(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.
24.如图①,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE.
将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)当α=0°和α=180°时,求的值.
(2)试判断当0°≤α<360°时,的大小有无变化?请仅就图②的情况给出证明.
(3)当△EDC旋转至A,D,E三点共线时,求线段BD的长.
答案
一、1.D 2.B 3.B 4.A 5.A 6.B
7.B 点拨:∵AB⊥BC,CD⊥BC,∴∠ABE=∠DCE=90°.
∵∠AEB=∠DEC,
∴△ABE∽△DCE.
∴=,即=.
∴AB=40
m.
8.B
9.B 点拨:设AB与OF相交于点M,
∵AF∥OB,
∴△FAM∽△OBM,
∴
=
=
=.
设S△BOM=S,则S△AOM=2S,
∵OC=FO,OM=FM,
∴OM=OC.
∴S△AOC=S△AOM=2S,
S△BOC=S△BOM=S.
∴S△ABO:S△AOC:S△BOC=3:2:1.
10.D 点拨:如果从30
cm长的一根中截,那么60
cm长的一根只能作为最长边,而△ABC的最长边也为60
cm,且另两边长之和大于30
cm,所以不符合题意.如果从60
cm长的一根中截,设截得的短边和长边的长分别为x
cm,y
cm,那么有三种情况,即20:30=50:x=60:y或20:x=50:30=60:y或20:x=50:y=60:30,解得x=75,y=90(x+y>60,不符合题意,舍去)或x=12,y=36或x=10,y=25.故选D.
二、11.
12.∠D=∠C(答案不唯一)
13.S1=S2 点拨:∵点C是线段AB的黄金分割点,且BC>AC,
∴BC2=AC·AB.
又∵S1=BC2,
S2=AC·AD=AC·AB,
∴S1=S2.
14.2;1:2;1:6
15.
16. 点拨:∵四边形CDEF是正方形,
∴CD=ED,DE∥CF,
设ED=x步,则CD=x步,AD=(12-x)步,
∵DE∥CF,
∴△ADE∽△ACB,
∴=,
∴=,∴x=.
∴该直角三角形能容纳的正方形边长最大是步.
17.或3 点拨:如图.
∵四边形ABCD为矩形,
?∴∠BAD=90°,
∴BD==10,
当PD=AD=8时,BP=BD-PD=2,
∵△PBE∽△DBC,
∴=,即=,
解得PE=,
当P′D=P′A时,点P′为BD的中点,∴P′E′=CD=3,
当PA=AD时,显然不成立.
故答案为或3.
18.× 点拨:在正三角形ABC中,AB1⊥BC,∴BB1=BC=1.
在Rt△ABB1中,AB1===,
根据题意可得△AB2B1∽△AB1B,记△AB1B的面积为S,
∴=.∴S1=S.
同理可得S2=S1,S3=S2,S4=S3,….
∵S=×1×=,
∴S1=S=×,
S2=S1=×,S3=S2=×,S4=S3=×,…,Sn=×.
三、19.解:∵四边形ABCD∽四边形EFGH,∴∠H=∠D=95°.
∴∠α=360°-95°-118°-67°=80°.
∵四边形ABCD∽四边形EFGH,
∴=,
∴x∶7=12∶6,解得x=14.
20.解:(1)如图.
(2)S△A′B′C′=4×4-×2×2-×2×4-×2×4=6.
21.(1)证明:∵AB=AC,∴∠B=∠C,
又∵AD为BC边上的中线,
∴AD⊥BC.
∵DE⊥AB,
∴∠BED=∠ADC=90°.
∴△BDE∽△CAD.
(2)解:∵BC=10,AD为BC边上的中线,
∴BD=CD=5.
∵AC=AB=13,
∴由勾股定理可知
AD==12.
由(1)中△BDE∽△CAD可知=,得=,故DE=.
22.解:过点E作EH⊥CD交CD于点H,交AB于点G,如图所示.
由题意得,EF⊥FD,AB⊥FD,
CD⊥FD.
∵EH⊥CD,EH⊥AB,
∴四边形EFDH为矩形,
∴EF=GB=DH=1.5米,EG=FB=2.5米,GH=BD=8米,
∴AG=AB-GB=2.4-1.5=0.9(米).
∵EH⊥CD,EH⊥AB,∴AG∥CH,
∴△AEG∽△CEH,∴=,
∴=,
解得CH=3.78米,
∴CD=CH+DH=3.78+1.5=5.28(米).
答:树高CD为5.28米.
23.解:(1)① ②或
(2)相似.理由:连接CD交EF于点O.
∵CD是Rt△ABC的中线,
∴CD=DB=AB,
∴∠DCB=∠B,
由折叠知∠COF=∠DOF=90°,
∴∠DCB+∠CFE=90°,
∴∠B+∠CFE=90°.
∵∠CEF+∠CFE=90°,
∴∠B=∠CEF.
在△CEF和△CBA中,∠ECF=∠BCA,∠CEF=∠B,
∴△CEF∽△CBA.
24.解:(1)当α=0°时,∵BC=2AB=8,∴AB=4.
∵点D,E分别是边BC,AC的中点,
∴BD=4,AE=EC=AC.
∵∠B=90°,
∴AC==4
,
∴AE=CE=2
,
∴==.
当α=180°时,如图①,
易得AC=4
,CE=2
,CD=4,
∴===.
(2)无变化.
证明:在题图①中,∵DE是△ABC的中位线,
∴DE∥AB,
∴=,∠EDC=∠B=90°.
在题图②中,∵△EDC在旋转过程中形状大小不变,
∴=仍然成立.
∵∠ACE=∠BCD=α,
∴△ACE∽△BCD.∴=.
由(1)可知AC=4
.
∴==.∴=.
∴的大小不变.
(3)当△EDC在BC上方,且A,D,E三点共线时,四边形ABCD为矩形,如图②,∴BD=AC=4
;当△EDC在BC下方,且A,E,D三点共线时,△ADC为直角三角形,如图③,由勾股定理可得AD==8.又知DE=2,∴AE=6.
∵=,∴BD=.
综上,BD的长为4
或.
一、选择题(每题3分,共30分)
1.若△ABC∽△A′B′C′,∠A=40°,∠B=60°,则∠C′等于( )
A.20°
B.40°
C.60°
D.80°
2.如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若=,则等于( )
A.
B.
C.
D.1
3.下列四组线段中,不是成比例线段的为( )
A.3,6,2,4
B.4,6,5,10
C.1,,,
D.2,,2
,
4.下列各组图形中有可能不相似的是( )
A.各有一个角是45°的两个等腰三角形
B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形
D.两个等腰直角三角形
5.如图,在平面直角坐标系中,有点A(6,3),B(6,0),以原点O为位似中心,位似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1)
B.(2,0)
C.(3,3)
D.(3,1)
6.下列说法:①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三角形斜边上的中线与斜边的比为1:2;④两个相似多边形的面积比为4:9,则周长的比为16:81.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
7.如图,为计算河的宽度(河两岸平行),在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一直线上,若测得BE=20
m,CE=10
m,CD=20
m,则河的宽度AB为( )
A.60
m
B.40
m
C.30
m
D.20
m
8.如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(6,0)
B.(6,3)
C.(6,5)
D.(4,2)
9.如图,四边形AOEF是平行四边形,点B为OE的中点,延长FO至点C,使OC=FO,连接AB,AC,BC,则在△ABC中,S△ABO:S△AOC:S△BOC等于( )
A.6:2:1
B.3:2:1
C.6:3:2
D.4:3:2
10.已知△ABC的三边长分别为20
cm,50
cm,60
cm,现要利用长度分别为30
cm和60
cm的细木条各一根,做一个与△ABC相似的三角形木架,要求以其中一根为一边,将另一根截下两段(允许有余料)作为另外两边,那么另两边的长度分别为( )
A.10
cm,25
cm
B.10
cm,36
cm或12
cm,36
cm
C.12
cm,36
cm
D.10
cm,25
cm或12
cm,36
cm
二、填空题(每题3分,共24分)
11.已知==≠0,则=________.
12.如图,∠1=∠2,添加一个条件____________使得△ADE∽△ACB.
13.如图,已知点C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形的面积,S2表示长为AD(AD=AB)、宽为AC的矩形的面积,则S1与S2的大小关系为____________.
14.如图,在△ABC中,D,E分别是AB和AC的中点,F是BC延长线上一点,DF平分CE于点G,CF=1,则BC=______,△ADE与△ABC的周长之比为________,△CFG与△BFD的面积之比为________.
15.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且=,则=________.
16.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形(如图),勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是________步.
17.矩形ABCD中,AB=6,BC=8,点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为____________.
18.如图,正三角形ABC的边长为2,以BC边上的高AB1为边作正三角形AB1C1,△ABC与△AB1C1公共部分的面积记为S1,再以正三角形AB1C1的边B1C1上的高AB2为边作正三角形AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2,……,以此类推,则Sn=______________(用含n的式子表示,n为正整数).
三、解答题(19~22题每题10分,23题12分,24题14分,共66分)
19.如图,四边形ABCD∽四边形EFGH,试求出x及∠α的大小.
20.如图,△ABC三个顶点的坐标分别为A(1,2),B(3,1),C(2,3),以原点O为位似中心,将△ABC放大为原来的2倍得△A′B′C′.
(1)在图中第一象限内画出符合要求的△A′B′C′(不要求写画法);
(2)计算△A′B′C′的面积.
21.如图,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.
(1)求证:△BDE∽△CAD;
(2)若AB=13,BC=10,求线段DE的长.
22.如图,竖立在B处的标杆AB=2.4米,在F处的观测者从E处看到标杆顶端A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8米,FB=2.5米,EF=1.5米,求树高CD.
23.如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上的某一点D处,折痕为EF(点E,F分别在边AC,BC上).
(1)若△CEF与△ABC相似.
①当AC=BC=2时,AD的长为________.
②当AC=3,BC=4时,AD的长为__________.
(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.
24.如图①,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE.
将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)当α=0°和α=180°时,求的值.
(2)试判断当0°≤α<360°时,的大小有无变化?请仅就图②的情况给出证明.
(3)当△EDC旋转至A,D,E三点共线时,求线段BD的长.
答案
一、1.D 2.B 3.B 4.A 5.A 6.B
7.B 点拨:∵AB⊥BC,CD⊥BC,∴∠ABE=∠DCE=90°.
∵∠AEB=∠DEC,
∴△ABE∽△DCE.
∴=,即=.
∴AB=40
m.
8.B
9.B 点拨:设AB与OF相交于点M,
∵AF∥OB,
∴△FAM∽△OBM,
∴
=
=
=.
设S△BOM=S,则S△AOM=2S,
∵OC=FO,OM=FM,
∴OM=OC.
∴S△AOC=S△AOM=2S,
S△BOC=S△BOM=S.
∴S△ABO:S△AOC:S△BOC=3:2:1.
10.D 点拨:如果从30
cm长的一根中截,那么60
cm长的一根只能作为最长边,而△ABC的最长边也为60
cm,且另两边长之和大于30
cm,所以不符合题意.如果从60
cm长的一根中截,设截得的短边和长边的长分别为x
cm,y
cm,那么有三种情况,即20:30=50:x=60:y或20:x=50:30=60:y或20:x=50:y=60:30,解得x=75,y=90(x+y>60,不符合题意,舍去)或x=12,y=36或x=10,y=25.故选D.
二、11.
12.∠D=∠C(答案不唯一)
13.S1=S2 点拨:∵点C是线段AB的黄金分割点,且BC>AC,
∴BC2=AC·AB.
又∵S1=BC2,
S2=AC·AD=AC·AB,
∴S1=S2.
14.2;1:2;1:6
15.
16. 点拨:∵四边形CDEF是正方形,
∴CD=ED,DE∥CF,
设ED=x步,则CD=x步,AD=(12-x)步,
∵DE∥CF,
∴△ADE∽△ACB,
∴=,
∴=,∴x=.
∴该直角三角形能容纳的正方形边长最大是步.
17.或3 点拨:如图.
∵四边形ABCD为矩形,
?∴∠BAD=90°,
∴BD==10,
当PD=AD=8时,BP=BD-PD=2,
∵△PBE∽△DBC,
∴=,即=,
解得PE=,
当P′D=P′A时,点P′为BD的中点,∴P′E′=CD=3,
当PA=AD时,显然不成立.
故答案为或3.
18.× 点拨:在正三角形ABC中,AB1⊥BC,∴BB1=BC=1.
在Rt△ABB1中,AB1===,
根据题意可得△AB2B1∽△AB1B,记△AB1B的面积为S,
∴=.∴S1=S.
同理可得S2=S1,S3=S2,S4=S3,….
∵S=×1×=,
∴S1=S=×,
S2=S1=×,S3=S2=×,S4=S3=×,…,Sn=×.
三、19.解:∵四边形ABCD∽四边形EFGH,∴∠H=∠D=95°.
∴∠α=360°-95°-118°-67°=80°.
∵四边形ABCD∽四边形EFGH,
∴=,
∴x∶7=12∶6,解得x=14.
20.解:(1)如图.
(2)S△A′B′C′=4×4-×2×2-×2×4-×2×4=6.
21.(1)证明:∵AB=AC,∴∠B=∠C,
又∵AD为BC边上的中线,
∴AD⊥BC.
∵DE⊥AB,
∴∠BED=∠ADC=90°.
∴△BDE∽△CAD.
(2)解:∵BC=10,AD为BC边上的中线,
∴BD=CD=5.
∵AC=AB=13,
∴由勾股定理可知
AD==12.
由(1)中△BDE∽△CAD可知=,得=,故DE=.
22.解:过点E作EH⊥CD交CD于点H,交AB于点G,如图所示.
由题意得,EF⊥FD,AB⊥FD,
CD⊥FD.
∵EH⊥CD,EH⊥AB,
∴四边形EFDH为矩形,
∴EF=GB=DH=1.5米,EG=FB=2.5米,GH=BD=8米,
∴AG=AB-GB=2.4-1.5=0.9(米).
∵EH⊥CD,EH⊥AB,∴AG∥CH,
∴△AEG∽△CEH,∴=,
∴=,
解得CH=3.78米,
∴CD=CH+DH=3.78+1.5=5.28(米).
答:树高CD为5.28米.
23.解:(1)① ②或
(2)相似.理由:连接CD交EF于点O.
∵CD是Rt△ABC的中线,
∴CD=DB=AB,
∴∠DCB=∠B,
由折叠知∠COF=∠DOF=90°,
∴∠DCB+∠CFE=90°,
∴∠B+∠CFE=90°.
∵∠CEF+∠CFE=90°,
∴∠B=∠CEF.
在△CEF和△CBA中,∠ECF=∠BCA,∠CEF=∠B,
∴△CEF∽△CBA.
24.解:(1)当α=0°时,∵BC=2AB=8,∴AB=4.
∵点D,E分别是边BC,AC的中点,
∴BD=4,AE=EC=AC.
∵∠B=90°,
∴AC==4
,
∴AE=CE=2
,
∴==.
当α=180°时,如图①,
易得AC=4
,CE=2
,CD=4,
∴===.
(2)无变化.
证明:在题图①中,∵DE是△ABC的中位线,
∴DE∥AB,
∴=,∠EDC=∠B=90°.
在题图②中,∵△EDC在旋转过程中形状大小不变,
∴=仍然成立.
∵∠ACE=∠BCD=α,
∴△ACE∽△BCD.∴=.
由(1)可知AC=4
.
∴==.∴=.
∴的大小不变.
(3)当△EDC在BC上方,且A,D,E三点共线时,四边形ABCD为矩形,如图②,∴BD=AC=4
;当△EDC在BC下方,且A,E,D三点共线时,△ADC为直角三角形,如图③,由勾股定理可得AD==8.又知DE=2,∴AE=6.
∵=,∴BD=.
综上,BD的长为4
或.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
