冀教版数学九年级上册 25.1 比例线段 课件(39张ppt)
文档属性
| 名称 | 冀教版数学九年级上册 25.1 比例线段 课件(39张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-02 00:00:00 | ||
图片预览










文档简介
(共39张PPT)
第25章
图形的相似
25.1
比例线段
1
课堂讲解
2
课时流程
逐点
导讲练
课堂小结
作业提升
两条线段的比
成比例线段
比例的性质
黄金分割
为了研究相似图形,我们先来探究成比例线段的
有关概念及性质.
1
知识点
两条线段的比
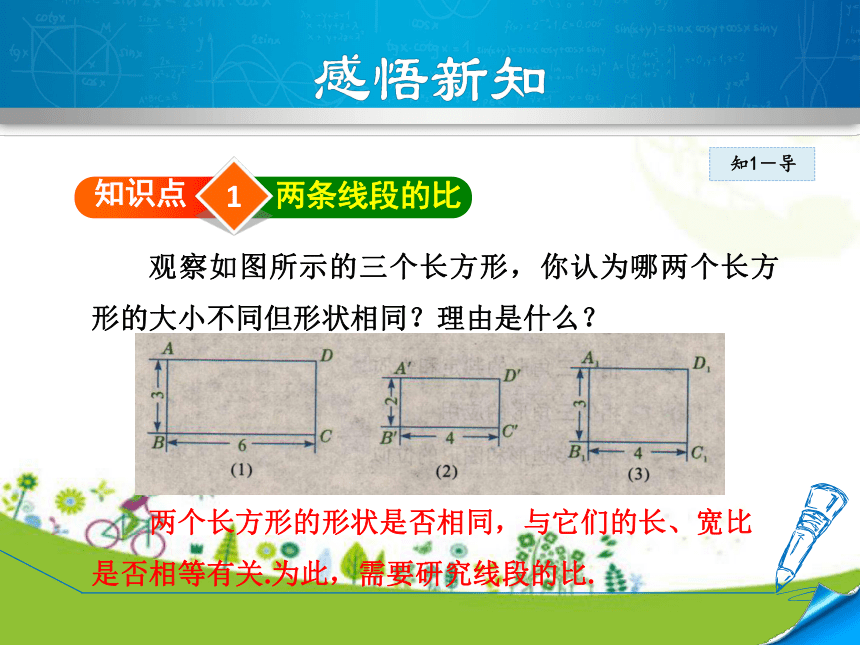
观察如图所示的三个长方形,你认为哪两个长方形的大小不同但形状相同?理由是什么?
知1-导
两个长方形的形状是否相同,与它们的长、宽比
是否相等有关.为此,需要研究线段的比.
知1-导
如果选用同一度量单位,量得线段a和b的长度分
别为m和n,我们就把m和n的比叫做线段a和b的比,记
作a∶b=m
∶
n,或
例如,如果
a=2
cm,b=3
cm,那么,a∶
b=2∶3.
知1-讲
1.线段的比没有单位;
2.线段的比是一个正数;
3.线段的比与所采用的长度单位无关;
4.线段的比必须是在同一长度单位下进行的.
知1-讲
若a=0.2
m,b=8
cm,则a∶
b=________.
例1
导引:
a=0.2
m=20
cm,a∶b=20∶8=5∶2.
5∶2
知1-讲
求线段的比时,两条线段的长度单位应该统一.
知1-练
1 在比例尺为1
∶
5
000的地图上,量得甲、乙两地的距离为25
cm,则甲、乙两地间的实际距离是( )
A.1
250
km
B.125
km
C.12.5
km
D.1.25
km
知1-练
2 正方形的对角线的长与它的边长之比是( )
A.2∶1
B.1∶2
C.1∶
D.
∶1
3 已知线段AB=20
cm,AC=10
dm,则AB∶AC=_____
2
知识点
成比例线段
知2-导
观察如图所示的三个长方形,你认为哪两个长方形的大小不同但形状相同?理由是什么?
两个长方形的形状是否相同,与它们的长、宽比
是否相等有关.为此,需要研究成比例线段.
知2-讲
1.定义:在四条线段a,b,c,d中,如果a与b的比等于
c与d的比,即
我们就把这四条线段叫做成比
例线段,简称比例线段.此时也称这四条线段成比例.
2.要点精析:定义中四条线段a,b,c,d是有先后顺序的.
3.易错提示:计算线段的比时切记不要忽略统一单位.
知2-讲
下列各组线段中,能成比例线段的是(
)
A.1
cm,3
cm,4
cm,6
cm
B.30
cm,12
cm,0.8
cm,0.2
cm
C.0.1
cm,0.2
cm,0.3
cm,0.4
cm
D.12
cm,16
cm,45
cm,60
cm
例2
D
知2-讲
导引:
从比例线段的概念入手.作为选择题,可逐个排查.
为了能迅速找到比例关系,可首先对数据按大小排
序,以减少试验的次数.
A中的
它们不成比例;
B中的
它们不成比例;
C中的
它们不成比例;
D中的
它们成比例.故选D.
知2-讲
方法技巧:
如果说四条线段a、b、c、d是成比例线段,则
这四条线段的顺序就确定了,也就是说,只能写成
这一种形式,而不能写成其他的形式.
知2-讲
判断四条线段是否是成比例线段的方法:先将线段的长度单位统一并按长度的大小排序,然后,判断前两条线段的比是否与后两条线段的比相等,或判断最长的线段与最短的线段的乘积是否与另外两条线段的乘积相等.若相等,则这四条线段为成比例线段;若不相等,则这四条线段不是成比例线段
知2-练
1 下列四组不同长度的线段中,不是成比例线段的一组是( )
A.1
cm,2
cm,3
cm,6
cm
B.2
cm,3
cm,4
cm,6
cm
C.1
cm,
D.1
cm,2
cm,3
cm,5
cm
知2-练
2 下列各组线段(单位:cm)中,是成比例线段的是( )
A.1,2,3,4
B.1,2,2,4
C.3,5,9,13
D.1,2,2,3
知2-练
3 四条线段a,b,c,d成比例,其中a=3
cm,d=4
cm,c=6
cm,则b等于( )
A.8
cm
B.
cm
C.
cm
D.2
cm
3
知识点
比例的性质
知3-导
如果线段a,b
,c,d成比例,那么ad和bc相等吗?
为什么?
反之,如果线段a,b
,c,d满足ad=bc,那么这四条线段成比例吗?
为什么?
知3-导
比例的基本性质
即b2=ac,就把b叫做a,c的比例中项.
知3-讲
问题
我们知道,由
可以得到
类
似地,如果
你认为
会有怎样的结果?
请说明理由.
知3-讲
事实上,若设
则有a=kb,c=
kd,···,m=kn.
所以a+c+···+m=kb+kd+···kn+=k(b+d+···+n).
因为b+d+···+n≠0,所以
即
知3-讲
若5x-4y=0,则
例3
从比例线段的性质入手.
根据比例的基本性质把5x-
4y=0变形为:
然后利用合比性质变形即得.
也可使用“设参数”的方式,代入后约分即可.
分析:
知3-讲
∵5x-4y=0,
∴
∴
令x=4k,y=5k,
则
解:
知3-讲
当有连等式时常用设参数的方法,实际上,当出
现比例时,设参数也是非常奏效的方法.
知3-练
1 若
,则
等于( )
A.
B.
C.
D.
2 【中考·东营】若
=
的值为( )
A.1
B.
C.
D.
知3-练
知3-练
3
已知△ABC中,BC∶AC∶AB=3∶5∶7,且AC+BC-AB=6,则△ABC的周长
为_______.
4
知识点
黄金分割
知4-导
如图,已知线段AB=a,点C在AB上.
当
时,线段AC的长是多少?
在上述问题中,设AC=x,建立关于x的方程x2+ax
—a2=0,可解得x=
取其正根,得
知4-讲
1.在线段AB上有一点C,如果点C把AB分成的两条线段
AC和BC满足
,那么称线段AB被点C黄金
分割,点C称为线段AB的黄金分割点,
称为黄
金比.其比值是
近似值是0.618.
2.每条线段上的黄金分割点都有两个.
知4-讲
已知线段AB=6
cm,点P为线段AB的黄金分割点,则线段AP的长为___________________________.
例4
一条线段有两个黄金分割点,∴要分两种情况计算.
当AP>PB时,
∵AB=6cm,
∴AP=
当AP<PB时,PB=
∴AP=AB-PB=(9-3
)cm.
错误答案:
错解分析:
知4-讲
本题运用了分类讨论思想,分AP是较短线段和较
长线段两种情况计算.
知4-练
1 如图,AB=2,点C是AB的黄金分割点,点D在AB上,且AD2=BD·AB,求
的值.
知4-练
2 如图所示,点C把线段AB分成两条线段AC,BC,且AC>BC,下列说法错误的是( )
A.如果
那么线段AB被点C黄金分割
B.如果AC2=AB·BC,那么线段AB被点C黄金分割
C.如果线段AB被点C黄金分割,则线段AC与AB的比叫做黄金比
D.如果线段AB被点C黄金分割,则
≈0.618
判断四条线段是否是成比例线段的方法:先将线
段长度统一单位并按长度的大小排序,然后,方法1,
判断前两条线段的比是否与后两条线段的比相等;方
法2,判断最长的线段与最短的线段的乘积是否与另外
两条线段的乘积相等.若相等,则这四条线段为成比
例线段;若不相等,则这四条线段为不成比例线
段.可简记为“一排(排顺序)、二算(算比值或乘积)、
三判(判断是否是成比例线段)”.
1.比例的基本性质:如果
那么ad=bc.
比例的基本性质反过来也成立,即:如果ad=bc,那
么
(b,d≠0),也可推得
(c,d≠0).
2.比例中项:如果
即b2=ac,我们就把b叫做a,
c的比例中项.
3.比例还有以下常用性质:
(1)合比性质:如果
那么
(2)分比性质:如果
那么
(3)合分比性质:如果
那么
(a≠b,
c≠d);
(4)等比性质:如果
(b+d+…+n≠0),
那么
完成教材P60练习T1-T3,
P61习题A组T1-T3,T14-T17
第25章
图形的相似
25.1
比例线段
1
课堂讲解
2
课时流程
逐点
导讲练
课堂小结
作业提升
两条线段的比
成比例线段
比例的性质
黄金分割
为了研究相似图形,我们先来探究成比例线段的
有关概念及性质.
1
知识点
两条线段的比
观察如图所示的三个长方形,你认为哪两个长方形的大小不同但形状相同?理由是什么?
知1-导
两个长方形的形状是否相同,与它们的长、宽比
是否相等有关.为此,需要研究线段的比.
知1-导
如果选用同一度量单位,量得线段a和b的长度分
别为m和n,我们就把m和n的比叫做线段a和b的比,记
作a∶b=m
∶
n,或
例如,如果
a=2
cm,b=3
cm,那么,a∶
b=2∶3.
知1-讲
1.线段的比没有单位;
2.线段的比是一个正数;
3.线段的比与所采用的长度单位无关;
4.线段的比必须是在同一长度单位下进行的.
知1-讲
若a=0.2
m,b=8
cm,则a∶
b=________.
例1
导引:
a=0.2
m=20
cm,a∶b=20∶8=5∶2.
5∶2
知1-讲
求线段的比时,两条线段的长度单位应该统一.
知1-练
1 在比例尺为1
∶
5
000的地图上,量得甲、乙两地的距离为25
cm,则甲、乙两地间的实际距离是( )
A.1
250
km
B.125
km
C.12.5
km
D.1.25
km
知1-练
2 正方形的对角线的长与它的边长之比是( )
A.2∶1
B.1∶2
C.1∶
D.
∶1
3 已知线段AB=20
cm,AC=10
dm,则AB∶AC=_____
2
知识点
成比例线段
知2-导
观察如图所示的三个长方形,你认为哪两个长方形的大小不同但形状相同?理由是什么?
两个长方形的形状是否相同,与它们的长、宽比
是否相等有关.为此,需要研究成比例线段.
知2-讲
1.定义:在四条线段a,b,c,d中,如果a与b的比等于
c与d的比,即
我们就把这四条线段叫做成比
例线段,简称比例线段.此时也称这四条线段成比例.
2.要点精析:定义中四条线段a,b,c,d是有先后顺序的.
3.易错提示:计算线段的比时切记不要忽略统一单位.
知2-讲
下列各组线段中,能成比例线段的是(
)
A.1
cm,3
cm,4
cm,6
cm
B.30
cm,12
cm,0.8
cm,0.2
cm
C.0.1
cm,0.2
cm,0.3
cm,0.4
cm
D.12
cm,16
cm,45
cm,60
cm
例2
D
知2-讲
导引:
从比例线段的概念入手.作为选择题,可逐个排查.
为了能迅速找到比例关系,可首先对数据按大小排
序,以减少试验的次数.
A中的
它们不成比例;
B中的
它们不成比例;
C中的
它们不成比例;
D中的
它们成比例.故选D.
知2-讲
方法技巧:
如果说四条线段a、b、c、d是成比例线段,则
这四条线段的顺序就确定了,也就是说,只能写成
这一种形式,而不能写成其他的形式.
知2-讲
判断四条线段是否是成比例线段的方法:先将线段的长度单位统一并按长度的大小排序,然后,判断前两条线段的比是否与后两条线段的比相等,或判断最长的线段与最短的线段的乘积是否与另外两条线段的乘积相等.若相等,则这四条线段为成比例线段;若不相等,则这四条线段不是成比例线段
知2-练
1 下列四组不同长度的线段中,不是成比例线段的一组是( )
A.1
cm,2
cm,3
cm,6
cm
B.2
cm,3
cm,4
cm,6
cm
C.1
cm,
D.1
cm,2
cm,3
cm,5
cm
知2-练
2 下列各组线段(单位:cm)中,是成比例线段的是( )
A.1,2,3,4
B.1,2,2,4
C.3,5,9,13
D.1,2,2,3
知2-练
3 四条线段a,b,c,d成比例,其中a=3
cm,d=4
cm,c=6
cm,则b等于( )
A.8
cm
B.
cm
C.
cm
D.2
cm
3
知识点
比例的性质
知3-导
如果线段a,b
,c,d成比例,那么ad和bc相等吗?
为什么?
反之,如果线段a,b
,c,d满足ad=bc,那么这四条线段成比例吗?
为什么?
知3-导
比例的基本性质
即b2=ac,就把b叫做a,c的比例中项.
知3-讲
问题
我们知道,由
可以得到
类
似地,如果
你认为
会有怎样的结果?
请说明理由.
知3-讲
事实上,若设
则有a=kb,c=
kd,···,m=kn.
所以a+c+···+m=kb+kd+···kn+=k(b+d+···+n).
因为b+d+···+n≠0,所以
即
知3-讲
若5x-4y=0,则
例3
从比例线段的性质入手.
根据比例的基本性质把5x-
4y=0变形为:
然后利用合比性质变形即得.
也可使用“设参数”的方式,代入后约分即可.
分析:
知3-讲
∵5x-4y=0,
∴
∴
令x=4k,y=5k,
则
解:
知3-讲
当有连等式时常用设参数的方法,实际上,当出
现比例时,设参数也是非常奏效的方法.
知3-练
1 若
,则
等于( )
A.
B.
C.
D.
2 【中考·东营】若
=
的值为( )
A.1
B.
C.
D.
知3-练
知3-练
3
已知△ABC中,BC∶AC∶AB=3∶5∶7,且AC+BC-AB=6,则△ABC的周长
为_______.
4
知识点
黄金分割
知4-导
如图,已知线段AB=a,点C在AB上.
当
时,线段AC的长是多少?
在上述问题中,设AC=x,建立关于x的方程x2+ax
—a2=0,可解得x=
取其正根,得
知4-讲
1.在线段AB上有一点C,如果点C把AB分成的两条线段
AC和BC满足
,那么称线段AB被点C黄金
分割,点C称为线段AB的黄金分割点,
称为黄
金比.其比值是
近似值是0.618.
2.每条线段上的黄金分割点都有两个.
知4-讲
已知线段AB=6
cm,点P为线段AB的黄金分割点,则线段AP的长为___________________________.
例4
一条线段有两个黄金分割点,∴要分两种情况计算.
当AP>PB时,
∵AB=6cm,
∴AP=
当AP<PB时,PB=
∴AP=AB-PB=(9-3
)cm.
错误答案:
错解分析:
知4-讲
本题运用了分类讨论思想,分AP是较短线段和较
长线段两种情况计算.
知4-练
1 如图,AB=2,点C是AB的黄金分割点,点D在AB上,且AD2=BD·AB,求
的值.
知4-练
2 如图所示,点C把线段AB分成两条线段AC,BC,且AC>BC,下列说法错误的是( )
A.如果
那么线段AB被点C黄金分割
B.如果AC2=AB·BC,那么线段AB被点C黄金分割
C.如果线段AB被点C黄金分割,则线段AC与AB的比叫做黄金比
D.如果线段AB被点C黄金分割,则
≈0.618
判断四条线段是否是成比例线段的方法:先将线
段长度统一单位并按长度的大小排序,然后,方法1,
判断前两条线段的比是否与后两条线段的比相等;方
法2,判断最长的线段与最短的线段的乘积是否与另外
两条线段的乘积相等.若相等,则这四条线段为成比
例线段;若不相等,则这四条线段为不成比例线
段.可简记为“一排(排顺序)、二算(算比值或乘积)、
三判(判断是否是成比例线段)”.
1.比例的基本性质:如果
那么ad=bc.
比例的基本性质反过来也成立,即:如果ad=bc,那
么
(b,d≠0),也可推得
(c,d≠0).
2.比例中项:如果
即b2=ac,我们就把b叫做a,
c的比例中项.
3.比例还有以下常用性质:
(1)合比性质:如果
那么
(2)分比性质:如果
那么
(3)合分比性质:如果
那么
(a≠b,
c≠d);
(4)等比性质:如果
(b+d+…+n≠0),
那么
完成教材P60练习T1-T3,
P61习题A组T1-T3,T14-T17
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
