冀教版数学九年级上册25.3 相似三角形 课件(35张ppt)
文档属性
| 名称 | 冀教版数学九年级上册25.3 相似三角形 课件(35张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-02 14:30:54 | ||
图片预览







文档简介
(共35张PPT)
第25章
图形的相似
25.3
相似三角形
1
课堂讲解
2
课时流程
逐点
导讲练
课堂小结
作业提升
相似三角形
平行线判定三角形相似
相似三角形性质的应用
对应角相等、对应边也相等的两个三角形为全等三
角形.相仿地,我们来学习相似三角形的有关知识.
1
知识点
相似三角形
知1-导
知1-导
对应角相等、对应边成比例的两个三角形叫做相似
三角形(similar
triangles).相似三角形对应边的比叫做
它们的相似比(similar
ratio)
.
知1-导
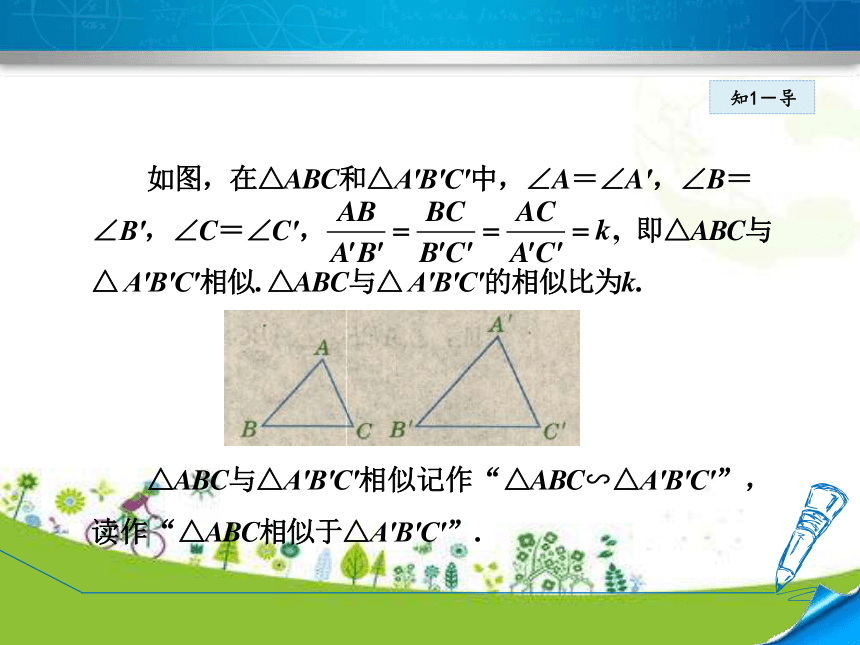
如图,在△ABC和△A′B′C′中,∠A=∠A′,∠B=
∠B′,∠C=∠C′,
即△ABC与
△
A′B′C′相似.
△ABC与△
A′B′C′的相似比为k.
△ABC与△A′B′C′相似记作“△ABC∽△A′B′C′”,
读作“△ABC相似于△A′B′C′”.
知1-讲
1.要点精析:
(1)若两个三角形相似,则三个角分别相等,三条边成
比例;
(2)相似三角形具有传递性:即
若△ABC∽△A′B′C′,△A′B′C′∽△A″B″C″,
则△ABC∽△A″B″C″;
(3)相似比为1的两个相似三角形全等,反过来两个全等
三角形是相似比为1的相似三角形.
知1-讲
2.易错警示:
(1)对应性:表示两三角形相似时,要注意对应性,即
要把对应顶点的字母写在对应位置上.
(2)顺序性:求两相似三角形的相似比时,要注意顺序
性.若当△ABC∽△A′B′C′时,
则△A′B′C′∽△ABC时,
知1-讲
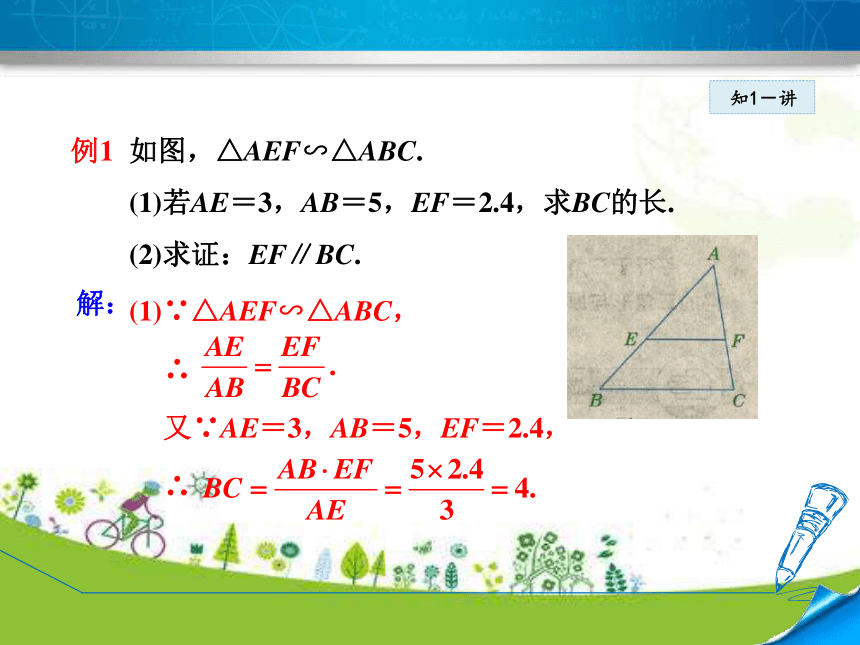
如图,△AEF∽△ABC.
(1)若AE=3,AB=5,EF=2.4,求BC的长.
(2)求证:EF∥BC.
(1)∵△AEF∽△ABC,
∴
又∵AE=3,AB=5,EF=2.4,
∴
例1
解:
知1-讲
(2)∵△AEF∽△ABC,
∴∠AEF=∠B.
∴BF∥BC.
知1-讲
根据相似三角形的定义进行判断,即证出三个角
分别相等,三条边成比例即可.
知1-练
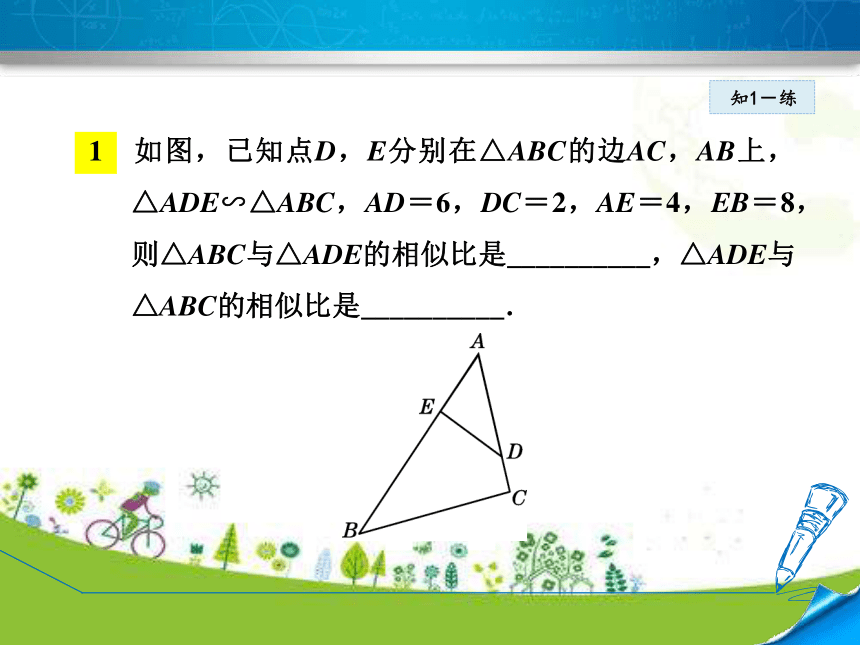
1 如图,已知点D,E分别在△ABC的边AC,AB上,△ADE∽△ABC,AD=6,DC=2,AE=4,EB=8,则△ABC与△ADE的相似比是__________,△ADE与△ABC的相似比是__________.
知1-练
2 如图,△ABC∽△AED,∠ADE=80°,∠A=60°,则∠C等于( )
A.40°
B.60°
C.80°
D.100°
知1-练
3 如图,△ABC∽△DEF,相似比为1∶2.若BC=1,则EF的长是( )
A.1
B.2
C.3
D.4
2
知识点
平行线判定三角形相似
知2-导
思考
如图,在△ABC中,DE∥BC,且DE分别交AB,AC于点D,E,△ADE与△ABC有什么关系?
知2-讲
我们知道,平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边成比例.进而可知,这样截得的三角形与原三角形相似.
已知:如图,
EF∥BC,与AB,AC(或它们的延长线)相交于点E,
F.
求证:△AEF∽△ABC.
知2-导
证明:
如图(1),在△AEF和△ABC中,
∵EF∥BC,
∴∠AEF=∠B,
∠AFE=∠C,
且
又∵∠A=∠A,
∴△AEF∽△ABC.
同理可证其他情况.
知2-导
平行于三角形一边的直线和其他两边(或它们的延
长线)相交,所截得的三角形与原三角形相似.
知2-讲
如图,在 ABCD中,F是AD边上的任意一点,连接BF并延长交CD的延长线于点E,连接AC,则图中与△DEF相似的三角形共有( )
A.1个
B.2个
C.3个
D.4个
例2
B
知2-讲
证明:
由于四边形ABCD是平行四边形,因此FD∥BC,
DE∥AB.于是可从图中找出符合“A”型相似的△DEF
与△CEB,符合“X”型相似的△DEF与△ABF.
故选B.
知2-讲
利用平行线寻找相似三角形的方法:在线段较多
的图形中寻找相似三角形,如果图中有线段平行的条
件,则集中精力在图形中寻找符合“A”型或“X”型的
基本图形,这不但是解本题的首要之选,也是今后解
本类题目的首要之选.
知2-练
1 如图,四边形ABCD的边AB,CD都平行于EF,BD交EF于点G,CG的延长线交AD于点H,则图中相似三角形有______对.
知2-练
2
【中考·河南】如图,在△ABC中,点D,E分别是AB,AC的中点,则下列结论:
①BC=2DE;②△ADE∽△ABC;③
其中正确的有( )
A.3个
B.2个
C.1个
D.0个
知2-练
3 如图,已知AB∥CD∥EF,则图中相似三角形有( )
A.0对
B.3对
C.2对
D.1对
3
知识点
相似三角形性质的应用
知3-导
如图所示,要测量一个池塘的
长是多少,不能直接测量的距离,
小明做了△ABC,取池塘的两个点
D,E,使DE∥BC,测出BC,AD,
AB的长就可以算出DE的长,你知道为什么吗?
原来由DE∥BC可以得到△ABC∽△ADE,
所以AD∶AB=DE∶BC
知3-导
通过建立相似三角形数学模型
可以解决实际问题
知3-讲
【中考·宁德】如图,在
ABCD中,AE=EB,AF=2,则FC=________.
例3
4
知3-讲
导引:
有平行四边形,就提供了平行线,就有三角形相
似,就有对应边的比相等,就能求出FC的长.
在
ABCD中,∵AB∥CD,AB=CD,
∴△AEF∽△CDF.
∴
∵AE=EB,∴
∴FC=2AF=4
知3-讲
求线段的长的方法:对于三角形被平行线所截形
成“A”型或“X”型的图形,当所求的线段或已知线段
在平行的边上时,通常考虑通过找三角形相似,再利
用相似三角形的对应边的比相等构建包含已知与未知
线段的比例式,即可求出线段的长;当所求的线段或
已知线段不在平行的边上时,则考虑直接用平行线截
线段成比例求线段的长.
知3-练
1
【中考·株洲】如图,已知AB,CD,EF都与BD垂直,垂足分别是B,D,F,且AB=1,CD=3,那么EF的长是( )
A.
B.
C.
D.
2 如图,AB∥CD,AD与BC相交于点O,那么在下列比例式中,正确的是( )
A.
B.
C.
D.
知3-练
3 【中考·毕节】如图,在△ABC中,DE∥BC,AE
∶
EC=2
∶
3,DE=4,则BC等于( )
A.10
B.8
C.9
D.6
知3-练
1.相似三角形的定义具有两种功能:判定和性质,即对
应边成比例、对应角相等?两个三角形相似,注意相
似比具有顺序性.
2.平行线截三角形相似的定理:
平行于三角形一边的直线和其他两边(或它们的延长线)
相交,所截得的三角形与原三角形相似.
数学表达式:如图,∵DE∥BC,
∴△ABC∽△ADE.
知3-讲
要点精析:根据定
理得到的相似三角
形的三个基本图形
中都有BC∥DE,图(1)(2)很像大写字母A,故我们称
之为“A”型相似;图(3)很像大写字母X,故我们称之
为“X”型相似(也像阿拉伯数字“8”).
3.作用:本定理是相似三角形判定定理的预备定理:它
通过平行证三角形相似,再由相似证对应角相等、对
应边成比例.
完成教材P71练习T1-T3
,习题A组T1-T3,
B组T1-T2
第25章
图形的相似
25.3
相似三角形
1
课堂讲解
2
课时流程
逐点
导讲练
课堂小结
作业提升
相似三角形
平行线判定三角形相似
相似三角形性质的应用
对应角相等、对应边也相等的两个三角形为全等三
角形.相仿地,我们来学习相似三角形的有关知识.
1
知识点
相似三角形
知1-导
知1-导
对应角相等、对应边成比例的两个三角形叫做相似
三角形(similar
triangles).相似三角形对应边的比叫做
它们的相似比(similar
ratio)
.
知1-导
如图,在△ABC和△A′B′C′中,∠A=∠A′,∠B=
∠B′,∠C=∠C′,
即△ABC与
△
A′B′C′相似.
△ABC与△
A′B′C′的相似比为k.
△ABC与△A′B′C′相似记作“△ABC∽△A′B′C′”,
读作“△ABC相似于△A′B′C′”.
知1-讲
1.要点精析:
(1)若两个三角形相似,则三个角分别相等,三条边成
比例;
(2)相似三角形具有传递性:即
若△ABC∽△A′B′C′,△A′B′C′∽△A″B″C″,
则△ABC∽△A″B″C″;
(3)相似比为1的两个相似三角形全等,反过来两个全等
三角形是相似比为1的相似三角形.
知1-讲
2.易错警示:
(1)对应性:表示两三角形相似时,要注意对应性,即
要把对应顶点的字母写在对应位置上.
(2)顺序性:求两相似三角形的相似比时,要注意顺序
性.若当△ABC∽△A′B′C′时,
则△A′B′C′∽△ABC时,
知1-讲
如图,△AEF∽△ABC.
(1)若AE=3,AB=5,EF=2.4,求BC的长.
(2)求证:EF∥BC.
(1)∵△AEF∽△ABC,
∴
又∵AE=3,AB=5,EF=2.4,
∴
例1
解:
知1-讲
(2)∵△AEF∽△ABC,
∴∠AEF=∠B.
∴BF∥BC.
知1-讲
根据相似三角形的定义进行判断,即证出三个角
分别相等,三条边成比例即可.
知1-练
1 如图,已知点D,E分别在△ABC的边AC,AB上,△ADE∽△ABC,AD=6,DC=2,AE=4,EB=8,则△ABC与△ADE的相似比是__________,△ADE与△ABC的相似比是__________.
知1-练
2 如图,△ABC∽△AED,∠ADE=80°,∠A=60°,则∠C等于( )
A.40°
B.60°
C.80°
D.100°
知1-练
3 如图,△ABC∽△DEF,相似比为1∶2.若BC=1,则EF的长是( )
A.1
B.2
C.3
D.4
2
知识点
平行线判定三角形相似
知2-导
思考
如图,在△ABC中,DE∥BC,且DE分别交AB,AC于点D,E,△ADE与△ABC有什么关系?
知2-讲
我们知道,平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边成比例.进而可知,这样截得的三角形与原三角形相似.
已知:如图,
EF∥BC,与AB,AC(或它们的延长线)相交于点E,
F.
求证:△AEF∽△ABC.
知2-导
证明:
如图(1),在△AEF和△ABC中,
∵EF∥BC,
∴∠AEF=∠B,
∠AFE=∠C,
且
又∵∠A=∠A,
∴△AEF∽△ABC.
同理可证其他情况.
知2-导
平行于三角形一边的直线和其他两边(或它们的延
长线)相交,所截得的三角形与原三角形相似.
知2-讲
如图,在 ABCD中,F是AD边上的任意一点,连接BF并延长交CD的延长线于点E,连接AC,则图中与△DEF相似的三角形共有( )
A.1个
B.2个
C.3个
D.4个
例2
B
知2-讲
证明:
由于四边形ABCD是平行四边形,因此FD∥BC,
DE∥AB.于是可从图中找出符合“A”型相似的△DEF
与△CEB,符合“X”型相似的△DEF与△ABF.
故选B.
知2-讲
利用平行线寻找相似三角形的方法:在线段较多
的图形中寻找相似三角形,如果图中有线段平行的条
件,则集中精力在图形中寻找符合“A”型或“X”型的
基本图形,这不但是解本题的首要之选,也是今后解
本类题目的首要之选.
知2-练
1 如图,四边形ABCD的边AB,CD都平行于EF,BD交EF于点G,CG的延长线交AD于点H,则图中相似三角形有______对.
知2-练
2
【中考·河南】如图,在△ABC中,点D,E分别是AB,AC的中点,则下列结论:
①BC=2DE;②△ADE∽△ABC;③
其中正确的有( )
A.3个
B.2个
C.1个
D.0个
知2-练
3 如图,已知AB∥CD∥EF,则图中相似三角形有( )
A.0对
B.3对
C.2对
D.1对
3
知识点
相似三角形性质的应用
知3-导
如图所示,要测量一个池塘的
长是多少,不能直接测量的距离,
小明做了△ABC,取池塘的两个点
D,E,使DE∥BC,测出BC,AD,
AB的长就可以算出DE的长,你知道为什么吗?
原来由DE∥BC可以得到△ABC∽△ADE,
所以AD∶AB=DE∶BC
知3-导
通过建立相似三角形数学模型
可以解决实际问题
知3-讲
【中考·宁德】如图,在
ABCD中,AE=EB,AF=2,则FC=________.
例3
4
知3-讲
导引:
有平行四边形,就提供了平行线,就有三角形相
似,就有对应边的比相等,就能求出FC的长.
在
ABCD中,∵AB∥CD,AB=CD,
∴△AEF∽△CDF.
∴
∵AE=EB,∴
∴FC=2AF=4
知3-讲
求线段的长的方法:对于三角形被平行线所截形
成“A”型或“X”型的图形,当所求的线段或已知线段
在平行的边上时,通常考虑通过找三角形相似,再利
用相似三角形的对应边的比相等构建包含已知与未知
线段的比例式,即可求出线段的长;当所求的线段或
已知线段不在平行的边上时,则考虑直接用平行线截
线段成比例求线段的长.
知3-练
1
【中考·株洲】如图,已知AB,CD,EF都与BD垂直,垂足分别是B,D,F,且AB=1,CD=3,那么EF的长是( )
A.
B.
C.
D.
2 如图,AB∥CD,AD与BC相交于点O,那么在下列比例式中,正确的是( )
A.
B.
C.
D.
知3-练
3 【中考·毕节】如图,在△ABC中,DE∥BC,AE
∶
EC=2
∶
3,DE=4,则BC等于( )
A.10
B.8
C.9
D.6
知3-练
1.相似三角形的定义具有两种功能:判定和性质,即对
应边成比例、对应角相等?两个三角形相似,注意相
似比具有顺序性.
2.平行线截三角形相似的定理:
平行于三角形一边的直线和其他两边(或它们的延长线)
相交,所截得的三角形与原三角形相似.
数学表达式:如图,∵DE∥BC,
∴△ABC∽△ADE.
知3-讲
要点精析:根据定
理得到的相似三角
形的三个基本图形
中都有BC∥DE,图(1)(2)很像大写字母A,故我们称
之为“A”型相似;图(3)很像大写字母X,故我们称之
为“X”型相似(也像阿拉伯数字“8”).
3.作用:本定理是相似三角形判定定理的预备定理:它
通过平行证三角形相似,再由相似证对应角相等、对
应边成比例.
完成教材P71练习T1-T3
,习题A组T1-T3,
B组T1-T2
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
