25.5相似三角形的性质课件(37张ppt)
文档属性
| 名称 | 25.5相似三角形的性质课件(37张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-03 09:19:20 | ||
图片预览








文档简介
(共37张PPT)
第25章
图形的相似
25.5
相似三角形的性质
1
课堂讲解
2
课时流程
逐点
导讲练
课堂小结
作业提升
相似三角形对应线段的比
相似三角形周长的比
相似三角形面积的比
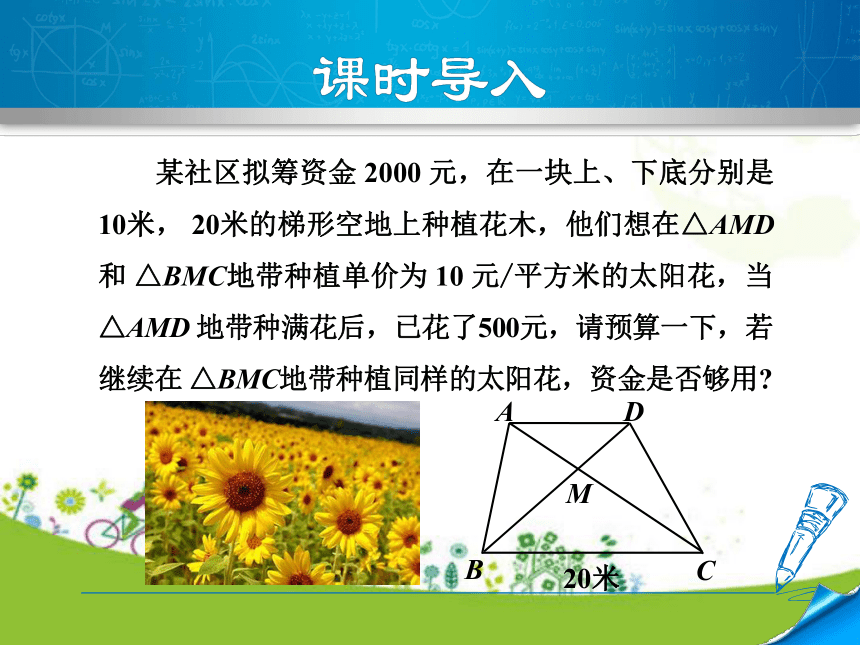
某社区拟筹资金
2000
元,在一块上、下底分别是
10米,
20米的梯形空地上种植花木,他们想在△AMD
和
△BMC地带种植单价为
10
元/平方米的太阳花,当
△AMD
地带种满花后,已花了500元,请预算一下,若
继续在
△BMC地带种植同样的太阳花,资金是否够用?
1
知识点
相似三角形对应线段的比
知1-讲
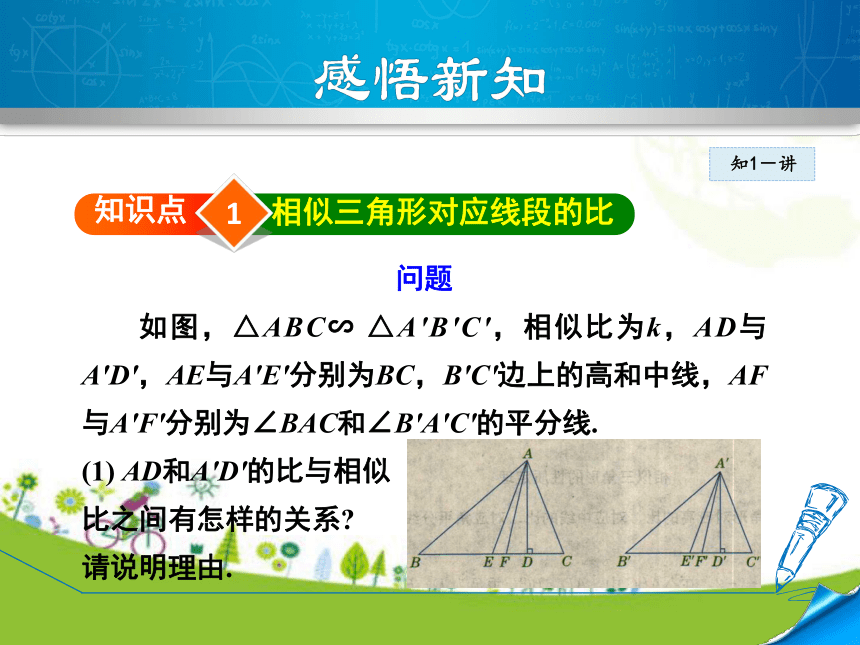
问题
如图,△ABC∽
△A′B′C′,相似比为k,AD与A′D′,AE与A′E′分别为BC,B′C′边上的高和中线,AF与A′F′分别为∠BAC和∠B′A′C′的平分线.
(1)
AD和A′D′的比与相似
比之间有怎样的关系?
请说明理由.
知1-讲
(2)AE和A′E′的比、AF和A′F′的比分别与相似比有怎样的关系?
请说明理由.
事实上,两个相似三角形的对应高、对应中线和对
应角平分线的比都等于它们的相似比.
下面,我们证明相似三角形对应高的比等于它们的
相似比.
知1-讲
已知:如图,△ABC∽△A′B′C′,相似比为k,AD、A′D′分别为BC,B′C′边上的高.
求证:
知1-讲
∵△ABC∽△A′B′C′
∴∠B=∠B′.
又∵AD⊥BC,
A′D′⊥B′C′,
∴∠ADB=∠A′D′B′=90°.
∴△ABD∽△A′B′D′.
∴
证明:
知1-讲
探究
1.已知:如图,△ABC∽△A′B′C′,相似比为k,AE,
A′E′分别为BC,B′C′边上的中线.求证:
2.已知:如图,△ABC∽△A′B′C′,相似比为k,AF,
A′F′分别为∠BAC,∠B′A′C′的平分线.
求证:
知1-讲
相似三角形的性质定理 相似三角形对应高的比、
对应中线的比、对应角平分线的比,都等于相似比.
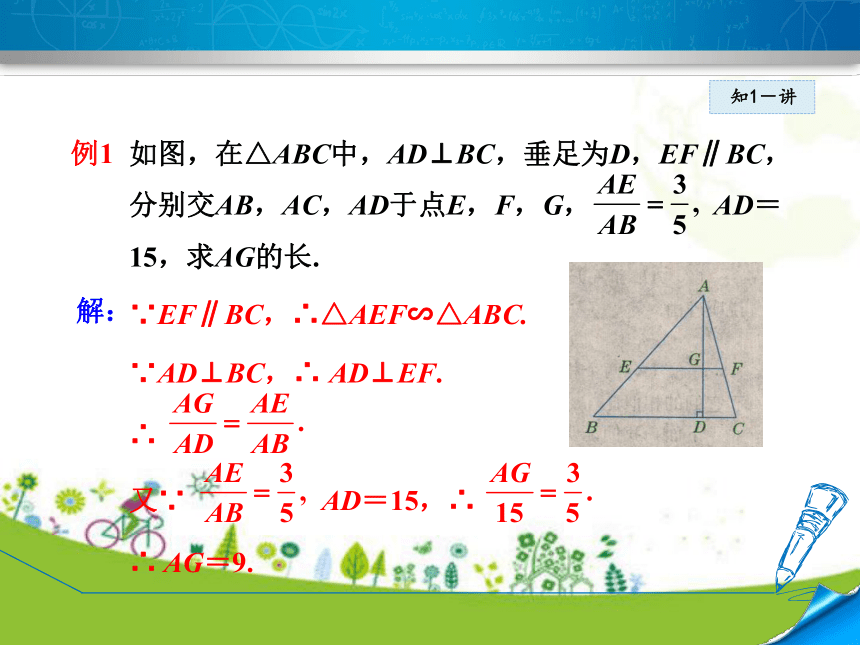
如图,在△ABC中,AD⊥BC,垂足为D,EF∥BC,分别交AB,AC,AD于点E,F,G,
AD=15,求AG的长.
∵EF∥BC,∴△AEF∽△ABC.
∵AD⊥BC,∴
AD⊥EF.
∴
又∵
AD=15,∴
∴
AG=9.
知1-讲
例1
解:
知1-讲
本题考查了相似三角形的性质,主要利用了相似
三角形对应高的比、对应中线的比等于相似比的性质,
熟记性质是解题的关键.
知1-练
1
已知△ABC∽△A′B′C′
,相似比为2∶3.
(1)如果AD,A′D′分别为这两个三角形的对应高,且AD=9
cm,求A′D′的长.
(2)如果AE,A′E′分别为这两个三角形的对应中线,且A′E′
=10
cm,求AE的长.
(3)如果AF,A′F′分别为这两个三角形的对应角平分线,求
的值.
知1-练
2
【中考·
兰州】已知△ABC∽△DEF,若△ABC与△DEF的相似比为
,则△ABC与△DEF对应中线的比为( )
A.
B.
C.
D.
知1-练
3 如图,已知△ADE∽△ABC,相似比为2∶5,则AF∶AG为( )
A.2∶5
B.5∶2
C.5∶1
D.1∶5
2
知识点
相似三角形周长的比
知2-讲
问题
某施工队在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽绿地被削去了一个角,变成了一个梯形,原绿化地一边AB的长由原来的30米缩短成18米.
现在的问题是:它的周长是多少?
知2-讲
将上面生活中的问题转化为数学问题是:
如图,已知DE∥BC,AB=30m,BD=18m,△ABC
的周长为80m,求△ADE的周长.
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴
由比例的性质可
解:
知2-讲
又∵△ADE
的周长=AD+AE+DE,
△ABC的周长=AB+AC+BC,
∴
∴△ADE
的周长=32米.
知2-讲
相似三角形周长的比等于相似比.
知2-讲
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D,则△BCD与△ABC的周长之比为( )
A.1∶2
B.1∶3
C.1∶4
D.1∶5
例2
A
知2-讲
导引:
在Rt△ABC中,∠A+∠B=90°;
在Rt△BCD中,∠BCD+∠B=90°,
所以∠BCD=∠A.
又因为∠B=∠B,所以△BCD∽△BAC.
在Rt△ABC中,∠A=30°,
所以
则△BCD与△ABC的周长比等于相
似比
知2-讲
相似三角形周长的比等于相似比在解题时,如果
是相似图形求周长就常用到周长比等于相似比.
知2-练
1 如图,△ABC和△EBD中, △ABC与△EBD的周长之差为10cm,求△ABC的周长.
知2-练
2
【中考·重庆】△ABC与△DEF的相似比为1∶4,则△ABC与△DEF的周长比为( )
A.1∶2
B.1∶3
C.1∶4
D.1∶16
知2-练
3 已知△ABC∽△DEF,相似比为3∶1,且△ABC的周长为18,则△DEF的周长为( )
A.2
B.3
C.6
D.54
3
知识点
相似三角形面积的比
知3-讲
问题
相似三角形面积的比,与它们的相似比之间有什么关系呢?
知3-讲
如图,△ABC∽△A′B′C′,相似比为k,AD、A′D′分别
为BC,B′C′边上的高.
(1)△ABC的面积和△A′B′C′的面积的比与他们的相似比
有什么关系?
请说明理由.
知3-讲
因为
所以
即△ABC与△A′B′C′的面积之比等于相似比的平方.
知3-讲
相似三角形面积的比等于相似比的平方.
知3-讲
如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点.
求:
(1)△DEF的周长与△ABC的周长之比.
(2)△DEF的面积与△ABC的面积之比.
例3
知3-讲
解:
∵D,E,F分别为BC,AC,AB的中点,
∴
DE∥AB,
EF∥BC,DF∥AC,
∴△DEF∽△ABC.
∴△DEF的周长与△ABC的周长之比为1∶2,
△DEF的面积与△ABC的面积之比为1∶4.
知3-讲
利用相似比求周长和面积时,先确定两个三角形
相似,然后找准相似比,利用“相似三角形周长的比
等于相似比,相似三角形面积的比等于相似比的平方”
解题.
警示:
不要误认为面积的比等于相似比.
知3-练
1
两个相似三角形的相似比为1∶5,则
(1)这两个相似三角形周长的比为___________.
(2)这两个相似三角形面积的比为___________.
2 △ABC∽△A′B′C′,其相似比为3∶4,△ABC的周长为24
cm.求△A′B′C′的周长.
3
【中考·临夏州】如果两个相似三角形的面积比是1∶4,那么它们的周长比是( )
A.1∶16
B.1∶4
C.1∶6
D.1∶2
知3-练
4
【中考·云南】如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B,如果△ABD的面积为15,那么△ACD的面积为( )
A.15
B.10
C.
D.5
知3-练
课堂总结
知识方法要点
关键总结
注意事项
相似三角形的对应高、对应中线、对应角平分线的比的性质
相似三角形的对应高的比、对应中线的比、对应角平分线的比都等于相似比;
注意相似比是有顺序的
相似三角形的周长和面积比的性质
相似三角形的周长比等于相似比,面积比等于相似比的平方
不要误认为面积比等于相似比,更不要根据面积求相似比时,不开方反而平方
方法规律总结
当相似三角形的问题中出现高、中线或角平分线
时,要考虑用相似三角形对应高的比、对应角平分线
的比、对应中线的比都等于相似比;当相似三角形中
出现周长或面积时,要考虑用相似三角形的周长比等
于相似比,面积比等于相似比的平方;相似多边形也
有周长比等于相似比,面积比等于相似比的平方的性
质,以后也可以直接利用
完成教材P71练习T1-T3
,习题A组T1-T3,
B组T1-T2
第25章
图形的相似
25.5
相似三角形的性质
1
课堂讲解
2
课时流程
逐点
导讲练
课堂小结
作业提升
相似三角形对应线段的比
相似三角形周长的比
相似三角形面积的比
某社区拟筹资金
2000
元,在一块上、下底分别是
10米,
20米的梯形空地上种植花木,他们想在△AMD
和
△BMC地带种植单价为
10
元/平方米的太阳花,当
△AMD
地带种满花后,已花了500元,请预算一下,若
继续在
△BMC地带种植同样的太阳花,资金是否够用?
1
知识点
相似三角形对应线段的比
知1-讲
问题
如图,△ABC∽
△A′B′C′,相似比为k,AD与A′D′,AE与A′E′分别为BC,B′C′边上的高和中线,AF与A′F′分别为∠BAC和∠B′A′C′的平分线.
(1)
AD和A′D′的比与相似
比之间有怎样的关系?
请说明理由.
知1-讲
(2)AE和A′E′的比、AF和A′F′的比分别与相似比有怎样的关系?
请说明理由.
事实上,两个相似三角形的对应高、对应中线和对
应角平分线的比都等于它们的相似比.
下面,我们证明相似三角形对应高的比等于它们的
相似比.
知1-讲
已知:如图,△ABC∽△A′B′C′,相似比为k,AD、A′D′分别为BC,B′C′边上的高.
求证:
知1-讲
∵△ABC∽△A′B′C′
∴∠B=∠B′.
又∵AD⊥BC,
A′D′⊥B′C′,
∴∠ADB=∠A′D′B′=90°.
∴△ABD∽△A′B′D′.
∴
证明:
知1-讲
探究
1.已知:如图,△ABC∽△A′B′C′,相似比为k,AE,
A′E′分别为BC,B′C′边上的中线.求证:
2.已知:如图,△ABC∽△A′B′C′,相似比为k,AF,
A′F′分别为∠BAC,∠B′A′C′的平分线.
求证:
知1-讲
相似三角形的性质定理 相似三角形对应高的比、
对应中线的比、对应角平分线的比,都等于相似比.
如图,在△ABC中,AD⊥BC,垂足为D,EF∥BC,分别交AB,AC,AD于点E,F,G,
AD=15,求AG的长.
∵EF∥BC,∴△AEF∽△ABC.
∵AD⊥BC,∴
AD⊥EF.
∴
又∵
AD=15,∴
∴
AG=9.
知1-讲
例1
解:
知1-讲
本题考查了相似三角形的性质,主要利用了相似
三角形对应高的比、对应中线的比等于相似比的性质,
熟记性质是解题的关键.
知1-练
1
已知△ABC∽△A′B′C′
,相似比为2∶3.
(1)如果AD,A′D′分别为这两个三角形的对应高,且AD=9
cm,求A′D′的长.
(2)如果AE,A′E′分别为这两个三角形的对应中线,且A′E′
=10
cm,求AE的长.
(3)如果AF,A′F′分别为这两个三角形的对应角平分线,求
的值.
知1-练
2
【中考·
兰州】已知△ABC∽△DEF,若△ABC与△DEF的相似比为
,则△ABC与△DEF对应中线的比为( )
A.
B.
C.
D.
知1-练
3 如图,已知△ADE∽△ABC,相似比为2∶5,则AF∶AG为( )
A.2∶5
B.5∶2
C.5∶1
D.1∶5
2
知识点
相似三角形周长的比
知2-讲
问题
某施工队在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽绿地被削去了一个角,变成了一个梯形,原绿化地一边AB的长由原来的30米缩短成18米.
现在的问题是:它的周长是多少?
知2-讲
将上面生活中的问题转化为数学问题是:
如图,已知DE∥BC,AB=30m,BD=18m,△ABC
的周长为80m,求△ADE的周长.
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴
由比例的性质可
解:
知2-讲
又∵△ADE
的周长=AD+AE+DE,
△ABC的周长=AB+AC+BC,
∴
∴△ADE
的周长=32米.
知2-讲
相似三角形周长的比等于相似比.
知2-讲
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D,则△BCD与△ABC的周长之比为( )
A.1∶2
B.1∶3
C.1∶4
D.1∶5
例2
A
知2-讲
导引:
在Rt△ABC中,∠A+∠B=90°;
在Rt△BCD中,∠BCD+∠B=90°,
所以∠BCD=∠A.
又因为∠B=∠B,所以△BCD∽△BAC.
在Rt△ABC中,∠A=30°,
所以
则△BCD与△ABC的周长比等于相
似比
知2-讲
相似三角形周长的比等于相似比在解题时,如果
是相似图形求周长就常用到周长比等于相似比.
知2-练
1 如图,△ABC和△EBD中, △ABC与△EBD的周长之差为10cm,求△ABC的周长.
知2-练
2
【中考·重庆】△ABC与△DEF的相似比为1∶4,则△ABC与△DEF的周长比为( )
A.1∶2
B.1∶3
C.1∶4
D.1∶16
知2-练
3 已知△ABC∽△DEF,相似比为3∶1,且△ABC的周长为18,则△DEF的周长为( )
A.2
B.3
C.6
D.54
3
知识点
相似三角形面积的比
知3-讲
问题
相似三角形面积的比,与它们的相似比之间有什么关系呢?
知3-讲
如图,△ABC∽△A′B′C′,相似比为k,AD、A′D′分别
为BC,B′C′边上的高.
(1)△ABC的面积和△A′B′C′的面积的比与他们的相似比
有什么关系?
请说明理由.
知3-讲
因为
所以
即△ABC与△A′B′C′的面积之比等于相似比的平方.
知3-讲
相似三角形面积的比等于相似比的平方.
知3-讲
如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点.
求:
(1)△DEF的周长与△ABC的周长之比.
(2)△DEF的面积与△ABC的面积之比.
例3
知3-讲
解:
∵D,E,F分别为BC,AC,AB的中点,
∴
DE∥AB,
EF∥BC,DF∥AC,
∴△DEF∽△ABC.
∴△DEF的周长与△ABC的周长之比为1∶2,
△DEF的面积与△ABC的面积之比为1∶4.
知3-讲
利用相似比求周长和面积时,先确定两个三角形
相似,然后找准相似比,利用“相似三角形周长的比
等于相似比,相似三角形面积的比等于相似比的平方”
解题.
警示:
不要误认为面积的比等于相似比.
知3-练
1
两个相似三角形的相似比为1∶5,则
(1)这两个相似三角形周长的比为___________.
(2)这两个相似三角形面积的比为___________.
2 △ABC∽△A′B′C′,其相似比为3∶4,△ABC的周长为24
cm.求△A′B′C′的周长.
3
【中考·临夏州】如果两个相似三角形的面积比是1∶4,那么它们的周长比是( )
A.1∶16
B.1∶4
C.1∶6
D.1∶2
知3-练
4
【中考·云南】如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B,如果△ABD的面积为15,那么△ACD的面积为( )
A.15
B.10
C.
D.5
知3-练
课堂总结
知识方法要点
关键总结
注意事项
相似三角形的对应高、对应中线、对应角平分线的比的性质
相似三角形的对应高的比、对应中线的比、对应角平分线的比都等于相似比;
注意相似比是有顺序的
相似三角形的周长和面积比的性质
相似三角形的周长比等于相似比,面积比等于相似比的平方
不要误认为面积比等于相似比,更不要根据面积求相似比时,不开方反而平方
方法规律总结
当相似三角形的问题中出现高、中线或角平分线
时,要考虑用相似三角形对应高的比、对应角平分线
的比、对应中线的比都等于相似比;当相似三角形中
出现周长或面积时,要考虑用相似三角形的周长比等
于相似比,面积比等于相似比的平方;相似多边形也
有周长比等于相似比,面积比等于相似比的平方的性
质,以后也可以直接利用
完成教材P71练习T1-T3
,习题A组T1-T3,
B组T1-T2
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
