冀教版数学九年级上册25.6相似三角形的应用课件(32张ppt)
文档属性
| 名称 | 冀教版数学九年级上册25.6相似三角形的应用课件(32张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-03 09:20:53 | ||
图片预览









文档简介
(共32张PPT)
第25章
图形的相似
25.6
相似三角形的应用
1
课堂讲解
2
课时流程
逐点
导讲练
课堂小结
作业提升
利用光照下的影子
利用工具
利用镜子反射
埃及金字塔到底有多高?
据史料记载:古希腊科学
家泰勒斯利用相似三角形的原理,借助金字塔在太阳光
线下形成的影子测出了金字塔的高度.你知道他是怎样
测量的吗?
今天我们就利用这些知识测量一些不能直接
测量的物体的高度吧!
1
知识点
利用光照下的影子
知1-导
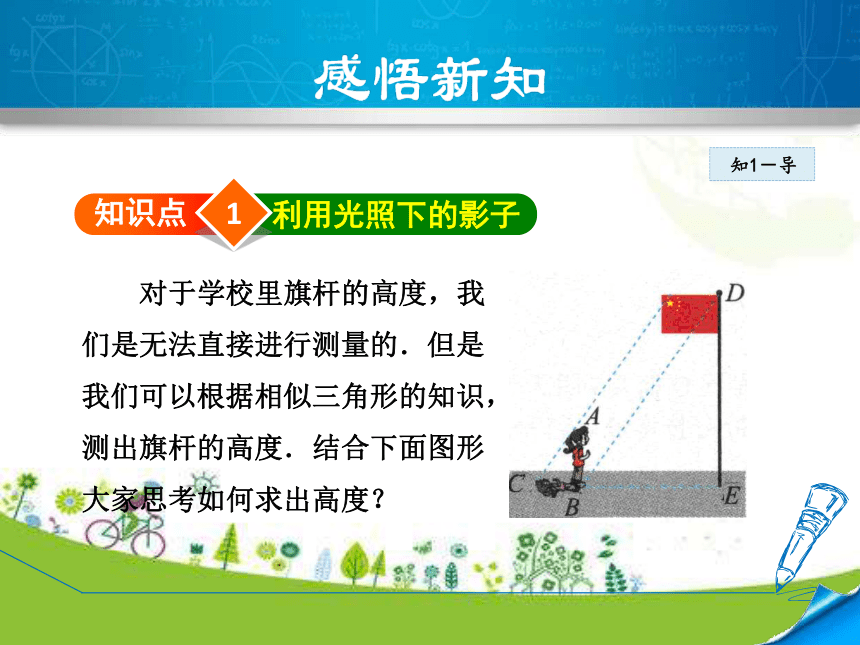
对于学校里旗杆的高度,我们是无法直接进行测量的.但是我们可以根据相似三角形的知识,测出旗杆的高度.结合下面图形大家思考如何求出高度?
知1-导
利用阳光下的影子测高:
(1)构造相似三角形,如图,
(2)测量数据:AB(身高),BC(人影长),BE(旗杆影长);
待求数据:DE(旗杆高).
(3)计算理由:因为AC∥DB(平行光),所以∠ACB=
∠DBE.
因为∠ABC=∠DEB=90°(直立即为垂直),
所以△ABC∽△DEB,有
知1-讲
1.测量方法:测量不能到达顶部的物体的高度时,常常
利用光线构造相似三角形(如同一时刻,物高与影长)
来解决.常见的测量方式有四种,如图所示.
知1-讲
2.要点精析:
(1)由于太阳在不停地移动,影子的长也随着太阳的移
动而发生变化.因此,测量影子的长一定要在同一
时刻下进行,否则就会影响结果的准确性.
(2)太阳离我们非常远,因此可以把太阳光线近似地看
成平行光线.
(3)此方法要求被测物体的底部可以到达,否则测不到
被测物体的影长,从而计算不出物体的高.
知1-讲
如何测量旗杆的高度,说明具体过程及原理.
具体过程:
(1)依据.同一时刻,物体的高度与其影长成比例.
(2)测量.如图,让一名身高为h的同学恰好站在旗
杆的影子的顶端,然后测量该同学的影长l1,同
时测量旗杆的影长l2.
例1
解:
知1-讲
(3)计算.
∵太阳光线是平行光线,∴AB∥CD,
∴∠ABC=∠DCE.
∵∠ACB=∠DEC=90°,
∴△ACB∽△DEC,
∵AC=h,BC=l1,EC=l2,
知1-讲
利用影长测量不能直接测量的物高(可到底部)的
方法:利用同一时刻的太阳光线构造两个相似三角形,
利用相似三角形对应边的比相等列出关于物高、物影、
人高、人影的比例关系式,然后通过测量物影、人高、
人影来计算出物高.
知1-练
1
【中考·陕西】小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:
如图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上
的影子重叠,且高度恰好相等,
此时,测得小明落在墙上的影子
高度CD=1.2m,CE=0.8m,CA
=30m(点A,E,C在同一条直线
上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB
(结果精确到0.1m).
知1-练
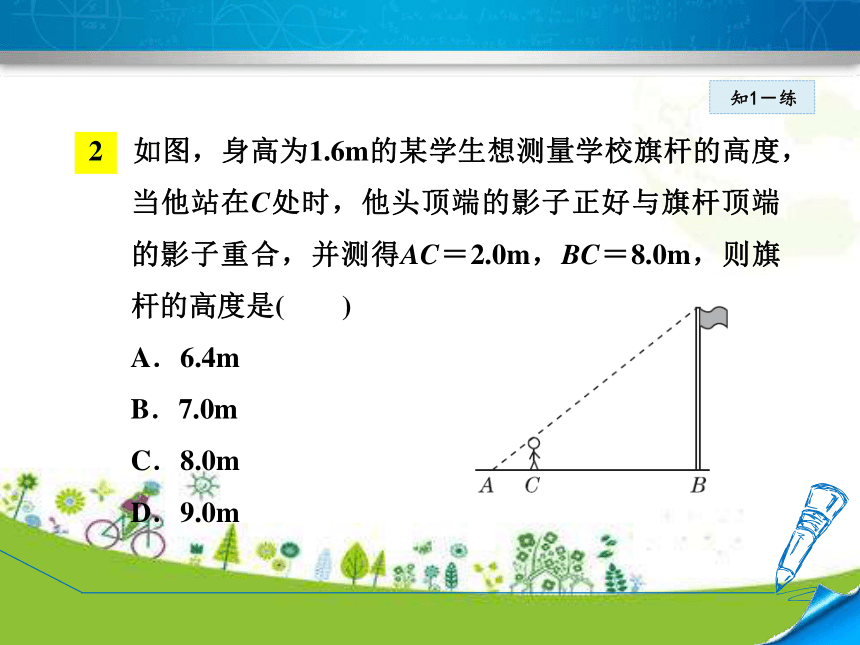
2 如图,身高为1.6m的某学生想测量学校旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0m,BC=8.0m,则旗杆的高度是( )
A.6.4m
B.7.0m
C.8.0m
D.9.0m
2
知识点
利用工具
知2-导
问题
小明想利用树影测量树高,他
在某一时刻测得长为1m的竹竿影长
0.9m,但当他马上测量树影时,因
树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,如下图,他先测得留在墙上的影高1.2m,又测得地面部分的影长2.7m,他求得的树高是多少?
知2-导
过点C作CE⊥AB于点E,因此BE=CD=1.2m,CE=
BD=2.7
m,由
可得AE=3
m,所以AB=
AE+BE=1.2+3=4.2
m.
这棵树的高度为4.2
m.
分析:
答案:
知2-讲
1.与测量有关的概念:
(1)视点:观察物体时人的眼睛称为视点.
(2)仰角:测量物体的高度时,水平视线与观察物
体的
视线间的夹称为仰角.
(3)盲区:人的视线看不到的区域称为盲区.
2.测量原理:用标杆和直尺作为三角形的边,利用视点
和盲区的知识构造相似三角形.
知2-讲
3.测量方法:如图,观察者的眼睛C必
须与标杆的顶端
D
和物体的顶端
A
“三点共线”,标杆与地面要垂直,
测量出标杆的高度DF,人眼离地面的高度CE,人与
标杆的距离EF,标杆与物体的距FG,利用相似三角
形“对应边的比相等”
的性质求物体的高度AG.
要点精析:利用标杆测量物体的高度也叫目测,在日常
生活中有着广泛的应用,必要时可
以用自己的身高和
臂长等作为测量工具.
知2-讲
如图,左、右并排的两棵大树的高分别为AB=8m和CD=12
m,两树底部的距离BD=5
m,一个人估计自己眼睛距地面1.6
m.
她沿着正对这两棵树的一条水平直路l从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C了?
例2
知2-讲
分析:
如图
(1),设观察者眼睛的位置为点F,画出观察
者的水平视线FG,分别交AB,
CD于点H,K.视
线FA与FG的夹角∠AFH是观察点A时的仰角.类
似地,∠CFK是观察点C时的仰角.由于树的遮挡,
区域I和II,观察者都看不到.
如图(2),假设观察者从左向右走到点E时,她的
眼睛的位置点E与两棵树的顶端A,C恰在一条直
线上.
解:
知2-讲
∵AB⊥l,CD
⊥l,∴AB∥CD.
∴△AEH∽△CEK.
∴
即
解得
EH=8m.
由此可知,如果观察者继续前进,当她与左
边的树的距离小于8
m时,由
于这棵树的遮挡,
她看不到右边树的顶端C.
知2-讲
测量高度和距离时,往往需要建立几何模型构造
相似三角形,利用相似三角形的性质直接求解或列方
程求解.
知2-练
1 如图,为测量电视塔AB的高度(包括台阶高),小亮在他与电视塔之间竖立一根5m高的标杆(即CE),当他距标杆2m时(即点D处),塔尖A、标杆的顶端E与小亮的眼睛F恰好在一条
直线上.
已知小亮的眼睛距
地面的高度是1.6m,标杆与
电视塔之间的距离是108
m.
求电视塔的高度.
知2-练
2
【中考·吉林】如图,利用标杆BE测量建筑物的高度,标杆BE高1.5m,测得AB=2m,BC=14m,则楼高CD为________.
3
知识点
利用镜子反射
知3-导
问题
若在一个阴天,没有太阳光,还能测量金字塔的高度吗?
知3-导
用镜面反射(如下图,点A是个小镜子,根据光
的反射定律:由入射角等于反射角构造相似三角形).
根据光的反射定律由入射角等于反射角构造△AOB
与△AFE相似,即可利用对应边的比相等求出BO.
分析:
知3-讲
利用相似三角形测量的一般步骤:
利用相似三角形的知识对未知量(高度、宽度等)进行测
量,一般要经历以下几个步骤:
(1)利用平行线、标杆等构造相似三角形;
(2)测量与表示未知量的线段相对应的边长以及另外任
意一组对应边的长度;
(3)画出示意图,利用相似三角形的性质,列出以上包
括未知量在内的四个量的比例式,解出未知量;
(4)检验并得出答案.
知3-讲
如图所示,小丽为了测量高楼MN的高度,在离N点20m的A处放了一个平面镜,小丽沿NA方向向后退到C点,正好从镜中看到楼顶M点.若AC等于1.5m,小丽的眼睛离地面的高度BC为1.6m,请你帮助小丽计算一下此楼的高度(精确到0.1m).
例3
导引:
根据反射角等于入射角,得到
△BCA与△MNA相似,列出比
例式,问题即可解决.
知3-讲
解:
如图,过点A作OA⊥CN,
∵BC⊥CA,MN⊥NA,
∴∠BCA=∠MNA=90°.
又∵∠BAO=∠MAO,
∴∠BAC=∠MAN.∴△BCA∽△MNA.
∴MN≈21.3m.
即此楼的高度约为21.3m.
知3-讲
测量不能直接到达的两点间的距离,关键是构造
两个相似三角形,利用能测量的三角形的边长及相似
三角形的性质求此距离.
知3-练
1 如图所示,小刚同学跳起将一个排球打在地面上,若他跳起的高度AB为1.8米,且排球弹起后正好碰到6.3米高的墙头D点(假设∠BPM=∠DPM,PM
⊥AC),而此时小刚距墙脚C点的距离正好是9米,试求排球落地点P距墙脚C点的距离.
2
【中考·天水】如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A发出经平面镜反射后刚好到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=2m,BP=3m,PD=12m,那么该古城墙的高度CD是________.
知3-练
知识总结
知识方法要点
关键总结
注意事项
利用相似三角形测高
根据
利用阳光下的影子测高
测量要尽量减少误差,取每种方法计算出的高度的平均
值,可使误差降到最小
方法规律总结
用相似三角形知识解决实际问题时的方法:
①
将实际问题转化为相似三角形问题;
②
构造出一对相似三角形;
③
根据相似三角形的性质,建立比例式,求出相应的量
完成教材P89练习T1-T2
,
P90习题T2,
P91练习T1-T2
第25章
图形的相似
25.6
相似三角形的应用
1
课堂讲解
2
课时流程
逐点
导讲练
课堂小结
作业提升
利用光照下的影子
利用工具
利用镜子反射
埃及金字塔到底有多高?
据史料记载:古希腊科学
家泰勒斯利用相似三角形的原理,借助金字塔在太阳光
线下形成的影子测出了金字塔的高度.你知道他是怎样
测量的吗?
今天我们就利用这些知识测量一些不能直接
测量的物体的高度吧!
1
知识点
利用光照下的影子
知1-导
对于学校里旗杆的高度,我们是无法直接进行测量的.但是我们可以根据相似三角形的知识,测出旗杆的高度.结合下面图形大家思考如何求出高度?
知1-导
利用阳光下的影子测高:
(1)构造相似三角形,如图,
(2)测量数据:AB(身高),BC(人影长),BE(旗杆影长);
待求数据:DE(旗杆高).
(3)计算理由:因为AC∥DB(平行光),所以∠ACB=
∠DBE.
因为∠ABC=∠DEB=90°(直立即为垂直),
所以△ABC∽△DEB,有
知1-讲
1.测量方法:测量不能到达顶部的物体的高度时,常常
利用光线构造相似三角形(如同一时刻,物高与影长)
来解决.常见的测量方式有四种,如图所示.
知1-讲
2.要点精析:
(1)由于太阳在不停地移动,影子的长也随着太阳的移
动而发生变化.因此,测量影子的长一定要在同一
时刻下进行,否则就会影响结果的准确性.
(2)太阳离我们非常远,因此可以把太阳光线近似地看
成平行光线.
(3)此方法要求被测物体的底部可以到达,否则测不到
被测物体的影长,从而计算不出物体的高.
知1-讲
如何测量旗杆的高度,说明具体过程及原理.
具体过程:
(1)依据.同一时刻,物体的高度与其影长成比例.
(2)测量.如图,让一名身高为h的同学恰好站在旗
杆的影子的顶端,然后测量该同学的影长l1,同
时测量旗杆的影长l2.
例1
解:
知1-讲
(3)计算.
∵太阳光线是平行光线,∴AB∥CD,
∴∠ABC=∠DCE.
∵∠ACB=∠DEC=90°,
∴△ACB∽△DEC,
∵AC=h,BC=l1,EC=l2,
知1-讲
利用影长测量不能直接测量的物高(可到底部)的
方法:利用同一时刻的太阳光线构造两个相似三角形,
利用相似三角形对应边的比相等列出关于物高、物影、
人高、人影的比例关系式,然后通过测量物影、人高、
人影来计算出物高.
知1-练
1
【中考·陕西】小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:
如图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上
的影子重叠,且高度恰好相等,
此时,测得小明落在墙上的影子
高度CD=1.2m,CE=0.8m,CA
=30m(点A,E,C在同一条直线
上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB
(结果精确到0.1m).
知1-练
2 如图,身高为1.6m的某学生想测量学校旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0m,BC=8.0m,则旗杆的高度是( )
A.6.4m
B.7.0m
C.8.0m
D.9.0m
2
知识点
利用工具
知2-导
问题
小明想利用树影测量树高,他
在某一时刻测得长为1m的竹竿影长
0.9m,但当他马上测量树影时,因
树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,如下图,他先测得留在墙上的影高1.2m,又测得地面部分的影长2.7m,他求得的树高是多少?
知2-导
过点C作CE⊥AB于点E,因此BE=CD=1.2m,CE=
BD=2.7
m,由
可得AE=3
m,所以AB=
AE+BE=1.2+3=4.2
m.
这棵树的高度为4.2
m.
分析:
答案:
知2-讲
1.与测量有关的概念:
(1)视点:观察物体时人的眼睛称为视点.
(2)仰角:测量物体的高度时,水平视线与观察物
体的
视线间的夹称为仰角.
(3)盲区:人的视线看不到的区域称为盲区.
2.测量原理:用标杆和直尺作为三角形的边,利用视点
和盲区的知识构造相似三角形.
知2-讲
3.测量方法:如图,观察者的眼睛C必
须与标杆的顶端
D
和物体的顶端
A
“三点共线”,标杆与地面要垂直,
测量出标杆的高度DF,人眼离地面的高度CE,人与
标杆的距离EF,标杆与物体的距FG,利用相似三角
形“对应边的比相等”
的性质求物体的高度AG.
要点精析:利用标杆测量物体的高度也叫目测,在日常
生活中有着广泛的应用,必要时可
以用自己的身高和
臂长等作为测量工具.
知2-讲
如图,左、右并排的两棵大树的高分别为AB=8m和CD=12
m,两树底部的距离BD=5
m,一个人估计自己眼睛距地面1.6
m.
她沿着正对这两棵树的一条水平直路l从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C了?
例2
知2-讲
分析:
如图
(1),设观察者眼睛的位置为点F,画出观察
者的水平视线FG,分别交AB,
CD于点H,K.视
线FA与FG的夹角∠AFH是观察点A时的仰角.类
似地,∠CFK是观察点C时的仰角.由于树的遮挡,
区域I和II,观察者都看不到.
如图(2),假设观察者从左向右走到点E时,她的
眼睛的位置点E与两棵树的顶端A,C恰在一条直
线上.
解:
知2-讲
∵AB⊥l,CD
⊥l,∴AB∥CD.
∴△AEH∽△CEK.
∴
即
解得
EH=8m.
由此可知,如果观察者继续前进,当她与左
边的树的距离小于8
m时,由
于这棵树的遮挡,
她看不到右边树的顶端C.
知2-讲
测量高度和距离时,往往需要建立几何模型构造
相似三角形,利用相似三角形的性质直接求解或列方
程求解.
知2-练
1 如图,为测量电视塔AB的高度(包括台阶高),小亮在他与电视塔之间竖立一根5m高的标杆(即CE),当他距标杆2m时(即点D处),塔尖A、标杆的顶端E与小亮的眼睛F恰好在一条
直线上.
已知小亮的眼睛距
地面的高度是1.6m,标杆与
电视塔之间的距离是108
m.
求电视塔的高度.
知2-练
2
【中考·吉林】如图,利用标杆BE测量建筑物的高度,标杆BE高1.5m,测得AB=2m,BC=14m,则楼高CD为________.
3
知识点
利用镜子反射
知3-导
问题
若在一个阴天,没有太阳光,还能测量金字塔的高度吗?
知3-导
用镜面反射(如下图,点A是个小镜子,根据光
的反射定律:由入射角等于反射角构造相似三角形).
根据光的反射定律由入射角等于反射角构造△AOB
与△AFE相似,即可利用对应边的比相等求出BO.
分析:
知3-讲
利用相似三角形测量的一般步骤:
利用相似三角形的知识对未知量(高度、宽度等)进行测
量,一般要经历以下几个步骤:
(1)利用平行线、标杆等构造相似三角形;
(2)测量与表示未知量的线段相对应的边长以及另外任
意一组对应边的长度;
(3)画出示意图,利用相似三角形的性质,列出以上包
括未知量在内的四个量的比例式,解出未知量;
(4)检验并得出答案.
知3-讲
如图所示,小丽为了测量高楼MN的高度,在离N点20m的A处放了一个平面镜,小丽沿NA方向向后退到C点,正好从镜中看到楼顶M点.若AC等于1.5m,小丽的眼睛离地面的高度BC为1.6m,请你帮助小丽计算一下此楼的高度(精确到0.1m).
例3
导引:
根据反射角等于入射角,得到
△BCA与△MNA相似,列出比
例式,问题即可解决.
知3-讲
解:
如图,过点A作OA⊥CN,
∵BC⊥CA,MN⊥NA,
∴∠BCA=∠MNA=90°.
又∵∠BAO=∠MAO,
∴∠BAC=∠MAN.∴△BCA∽△MNA.
∴MN≈21.3m.
即此楼的高度约为21.3m.
知3-讲
测量不能直接到达的两点间的距离,关键是构造
两个相似三角形,利用能测量的三角形的边长及相似
三角形的性质求此距离.
知3-练
1 如图所示,小刚同学跳起将一个排球打在地面上,若他跳起的高度AB为1.8米,且排球弹起后正好碰到6.3米高的墙头D点(假设∠BPM=∠DPM,PM
⊥AC),而此时小刚距墙脚C点的距离正好是9米,试求排球落地点P距墙脚C点的距离.
2
【中考·天水】如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A发出经平面镜反射后刚好到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=2m,BP=3m,PD=12m,那么该古城墙的高度CD是________.
知3-练
知识总结
知识方法要点
关键总结
注意事项
利用相似三角形测高
根据
利用阳光下的影子测高
测量要尽量减少误差,取每种方法计算出的高度的平均
值,可使误差降到最小
方法规律总结
用相似三角形知识解决实际问题时的方法:
①
将实际问题转化为相似三角形问题;
②
构造出一对相似三角形;
③
根据相似三角形的性质,建立比例式,求出相应的量
完成教材P89练习T1-T2
,
P90习题T2,
P91练习T1-T2
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
