沪科版数学九年级上册第22章相似形达标测试卷 含答案
文档属性
| 名称 | 沪科版数学九年级上册第22章相似形达标测试卷 含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 460.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-02 18:12:13 | ||
图片预览




文档简介
第22章达标测试卷
一、选择题(每题4分,共40分)
1.下面给出的图形是相似图形的有( )
A.两张孪生兄弟的照片
B.三角板的内、外三角形
C.行书的“中”与楷书的“中”
D.同一棵树上摘下的两片树叶
2.在△ABC中,点D,E分别为边AB,AC的中点,则四边形BDEC与△ABC的面积之比为( )
A.1:2
B.1:3
C.3:4
D.1:4
3.如图,AD是直角三角形ABC斜边上的中线,AE⊥AD交CB的延长线于E,则图中一定相似的三角形是( )
A.△AED与△ACB
B.△AEB与△ACD
C.△BAE与△ACE
D.△AEC与△DAC
4.如图,在平面直角坐标系中,有点A(6,3),B(6,0),以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1)
B.(2,0)
C.(3,3)
D.(3,1)
5.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.某女模特身高165
cm,下半身长x(cm)与身高l(cm)的比值是0.60.为尽可能达到美的效果,她应穿的高跟鞋的高度大约为( )
A.4
cm
B.6
cm
C.8
cm
D.10
cm
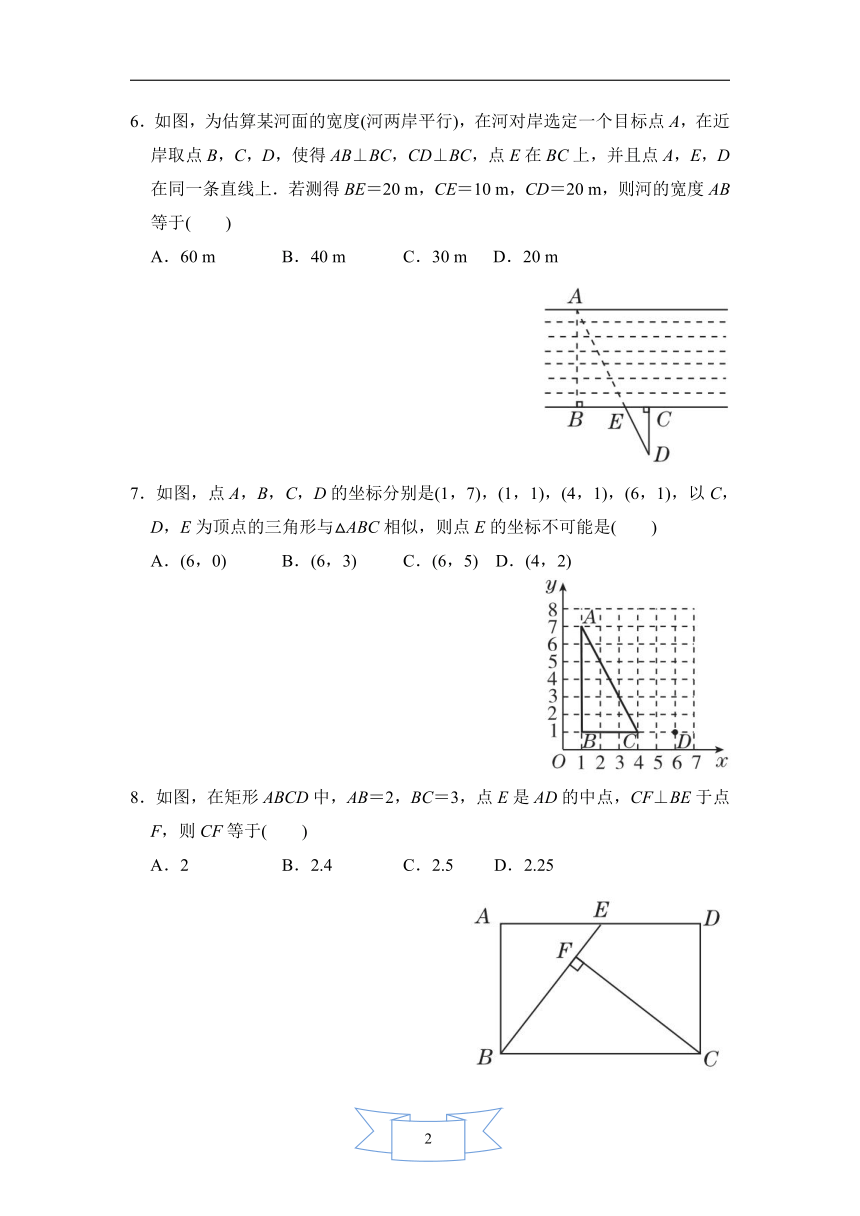
6.如图,为估算某河面的宽度(河两岸平行),在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20
m,CE=10
m,CD=20
m,则河的宽度AB等于( )
A.60
m
B.40
m
C.30
m
D.20
m
7.如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(6,0)
B.(6,3)
C.(6,5)
D.(4,2)
8.如图,在矩形ABCD中,AB=2,BC=3,点E是AD的中点,CF⊥BE于点F,则CF等于( )
A.2
B.2.4
C.2.5
D.2.25
9.如图,在平行四边形ABCD中,E是CD上的一点,DE:EC=2:3,连接AE,BE,BD,且AE,BD交于点F,则S△DEF:S△EBF:S△ABF=( )
A.2:5:25
B.4:9:25
C.2:3:5
D.4:10:25
10.如图,在△ABC中,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论有( )
A.1个
B.2个
C.3个
D.4个
二、填空题(每题5分,共20分)
11.假期,爸爸带小明去A地旅游.小明想知道他所居住的城市与A地之间的距离,他在比例尺为1:500
000的地图上测得所居住的城市距A地32
cm,则小明所居住的城市与A地之间的实际距离为________km.
12.如图,已知点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP,垂足是点B,若在射线BF上找一点M,使以点B,M,C为顶点的三角形与△ABP相似,则BM的长为________.
13.如图,小明把手臂水平向前伸直,手持小尺竖直,瞄准小尺的两端E,F,不断调整站立的位置,使其站立在点D处恰好能看到铁塔的顶部B和底部A,设小明的手臂长l=45
cm,小尺长a=15
cm,点D到铁塔底部A的距离AD=42
m,则铁塔的高度是________m.
14.如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1,再以正△AB1C1的边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2,…,以此类推,则Sn=________.(用含n的式子表示)
三、解答题(15题~18题,每题8分,19,20题,每题10分,21,22题,每题12分,23题14分,共90分)
15.若==≠0,且3x+2y-z=14,求x,y,z的值.
16.如图,在△ABC中,AB=8,BC=4,CA=6,CD∥AB,BD是∠ABC的平分线,BD交AC于点E,求AE的长.
17.如图,在边长为a的正方形ABCD中,M是AD的中点,能否在边AB上找一点N(不与A,B重合),使得△CDM与△MAN相似?若能,请求出AN的长;若不能,请说明理由.
18.如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
(1)求证:△ADE≌△CFE;
(2)若GB=2,BC=4,BD=1,求AB的长.
19.如图,已知在矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,=,△CEF的面积为S1,△AEB的面积为S2,求的值.
20.如图,在边长为1个单位长度的小正方形网格中:
(1)画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1;
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2BC2,请在网格中画出△A2BC2;
(3)求△CC1C2的面积.
21.如图,花丛中有一路灯杆AB.在灯光下,小明在D点处的影长DE=3
m,沿BD方向行走到达G点,DG=5
m,这时小明的影长GH=5
m.如果小明的身高为1.7
m,求路灯杆AB的高度(结果精确到0.1
m).
22.如图,在矩形ABCD中,AB=12
cm,BC=6
cm,点P沿AB边从点A开始向点B以2
cm/s的速度移动,点Q沿DA边从点D开始向点A以1
cm/s的速度移动.如果P,Q同时出发,用t(s)表示移动的时间(0≤t≤6),那么:
(1)当t为何值时,△QAP是等腰直角三角形?
(2)根据四边形QAPC的面积的计算结果,能得出什么结论?
(3)当t为何值时,以点Q,A,P为顶点的三角形与△ABC相似?
23.如图①,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE.
将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)当α=0°和α=180°时,求的值.
(2)试判断当0°≤α<360°时,的值有无变化?请仅就图②的情况给出证明.
(3)当△EDC旋转至A,D,E三点共线时,求线段BD的长.
答案
一、1.B 2.C 3.C 4.A 5.C
6.B 点拨:∵AB⊥BC,CD⊥BC,∴∠ABE=∠DCE=90°.
又∵∠AEB=∠DEC,
∴△ABE∽△DCE.
∴=,即=.
∴AB=40
m.
7.B
8.B 点拨:由∠A=∠ABC=90°,CF⊥BE,易证△ABE∽△FCB.
∴=.由AE=×3=1.5,
AB=2,易得BE=2.5,
∴=.∴CF=2.4.
9.D
10.D 点拨:∵四边形ADEF为正方形,∴∠FAD=90°,AD=AF=EF,
∴∠CAD+∠FAG=90°.
∵FG⊥CA,
∴∠G=90°=∠ACB.
∴∠AFG+∠FAG=90°.
∴∠DAC=∠AFG.
在△FGA和△ACD中,
∴△FGA≌△ACD(AAS).
∴AC=FG.故①正确.
∵BC=AC,
∴FG=BC.
∵∠ACB=90°,FG⊥CA,
∴FG∥BC.
∴四边形CBFG是矩形.
∴∠CBF=90°,S△FAB=FB·FG=S四边形CBFG.故②正确.
∵CA=CB,∠C=∠CBF=90°,
∴∠ABC=∠ABF=45°.故③正确.
易知∠FQE=∠DQB=∠ADC,∠E=∠C=90°,
∴△ACD∽△FEQ,
∴AC∶AD=FE∶FQ.
∴AD·FE=AD2=FQ·AC.故④正确.
二、11.160 点拨:设小明所居住的城市与A地之间的实际距离为x
km,根据题意可列比例式为=,解得x=160.
12.或3 点拨:由题意得∠ABC=∠FBP=90°,∴∠ABP=∠CBF.当△MBC∽△ABP时,BM:AB=BC:BP,得BM=4×4÷3=;当△CBM∽△ABP时,BM:BP=CB:AB,得BM=4×3÷4=3.
13.14 点拨:过点C作CH⊥AB于点H,交EF于点P,如图,则CH=DA=42
m,由题意知,CP=45
cm=0.45
m,EF=15
cm=0.15
m.
∵EF∥AB,
∴∠CEF=∠CBA,∠CFE=∠CAB.
∴△CEF∽△CBA.
∴=,即=.
∴AB=14
m,即铁塔的高度是14
m.
14.× 点拨:在正△ABC中,AB1⊥BC,∴BB1=BC=1.在Rt△ABB1中,AB1===,
根据题意可得△AB2B1∽△AB1B,记△AB1B的面积为S,∴=.∴S1=S.
同理可得S2=S1,S3=S2,S4=S3,…,Sn=Sn-1.
又∵S=×1×=,
∴S1=S=×,S2=S1=×,
S3=S2=×,
S4=S3=×,
…,
Sn=×.
三、15.解:设===k(k≠0),
则x=2k,y=3k,z=5k,
∵3x+2y-z=14,
∴6k+6k-5k=14,解得k=2,
∴x=4,y=6,z=10.
16.解:∵BD是∠ABC的平分线,
∴∠ABD=∠CBD,
∵AB∥CD,∴∠D=∠ABD,
∴∠D=∠CBD,∴BC=CD,
∵BC=4,∴CD=4,
又∵∠AEB=∠CED,
∴△ABE∽△CDE,
∴=,∴=,
∴AE=2CE,∵AC=6=AE+CE,
∴AE=4.
17.解:分两种情况讨论:
(1)若△CDM∽△MAN,则=.
∵正方形ABCD的边长为a,M是AD的中点,∴AN=a.
(2)若△CDM∽△NAM,则=.∵正方形ABCD的边长为a,M是AD的中点,∴AN=a,即N点与B点重合,不符合题意.
∴能在边AB上找一点N(不与A,B重合),使得△CDM与△MAN相似,此时AN=a.
18.(1)证明:∵AB∥FC,
∴∠A=∠ECF.
又∵∠AED=∠CEF,
且DE=FE,
∴△ADE≌△CFE(AAS).
(2)解:方法一 ∵AB∥FC,
∴∠GBD=∠GCF,∠GDB=∠F.
∴△GBD∽△GCF.
∴=.
∴=.
∴CF=3.
由(1)得△ADE≌△CFE,
∴AD=CF=3.
∴AB=AD+BD=3+1=4.
方法二 如图,取BC的中点H,连接EH.
∵△ADE≌△CFE,∴AE=CE.
∴EH是△ABC的中位线.
∴EH∥AB,且EH=AB.
∴∠GBD=∠GHE,∠GDB=∠GEH.∴△GBD∽△GHE.
∴=.∴=.
∴EH=2.∴AB=2EH=4.
19.解:∵BF⊥AC,
∴∠ACB+∠CBF=90°,
∵四边形ABCD为矩形,
∴∠BCF=∠ABC=90°,AB∥CD,AD=BC.
∴∠CAB+∠ACB=90°.∴∠CAB=∠CBF.
∴△FCB∽△CBA.∴CF:CB=CB:AB,
又∵=,
∴CF:CB=CB:AB=AD:AB=1:2.
∴FC:AB=1:4.
∵FC∥AB,∴△FCE∽△BAE.
∴===.
20.解:(1)如图所示.
(2)如图所示.
(3)如图,△CC1C2的面积为×3×6=9.
21.解:根据题意得AB⊥BH,CD⊥BH,FG⊥BH.
在Rt△ABE和Rt△CDE中,
∵AB⊥BH,CD⊥BH,∴CD∥AB,
可证得△CDE∽△ABE.
∴=
,①
同理得=,②
又∵CD=FG=1.7
m,
由①②可得
=,
即=,
解之得BD=7.5
m,
将BD=7.5
m代入①得
AB=5.95
m≈6.0
m.
故路灯杆AB的高度约为6.0
m.
22.解:(1)由题意知AP=2t,DQ=t,QA=6-t,当QA=AP时,
△QAP是等腰直角三角形,
∴6-t=2t,解得t=2.
∴当t=2时,△QAP是等腰直角三角形.
(2)四边形QAPC的面积=S△QAC+S△APC=AQ·AB+AP·BC=(36-6t)+6t=36.由计算结果发现:在P,Q两点移动的过程中,四边形QAPC的面积始终保持不变.
(3)分两种情况:
①当=时,△QAP∽△ABC,则=,即t=1.2;
②当=时,△PAQ∽△ABC,则=,即t=3.
∴当t=1.2或t=3时,以点Q,A,P为顶点的三角形与△ABC相似.
23.解:(1)当α=0°时,∵BC=2AB=8,∴AB=4.∵点D,E分别是边BC,AC的中点,∴BD=4,AE=EC=AC.∵∠B=90°,
∴AC==4
,
∴AE=CE=2
,
∴==.
当α=180°时,如图①,
易得AC=4
,CE=2
,CD=4,
∴===.
(2)无变化.
证明:在题图①中,∵DE是△ABC的中位线,
∴DE∥AB,
∴=,∠EDC=∠B=90°.
如题图②,∵△EDC在旋转过程中的形状和大小不变,
∴=仍然成立.
又∵∠ACE=∠BCD=α,
∴△ACE∽△BCD.∴=.
在Rt△ABC中,AC===4
.
∴==.∴=.
∴的值无变化.
(3)当△EDC在BC的上方,且A,D,E三点共线时,四边形ABCD为矩形,如图②,∴BD=AC=4
;当△EDC在BC的下方,且A,E,D三点共线时,△ADC为直角三角形,如图③,由勾股定理可得AD==8.又易知DE=2,
∴AE=6.∵=,∴BD=.
综上,BD的长为4
或.
一、选择题(每题4分,共40分)
1.下面给出的图形是相似图形的有( )
A.两张孪生兄弟的照片
B.三角板的内、外三角形
C.行书的“中”与楷书的“中”
D.同一棵树上摘下的两片树叶
2.在△ABC中,点D,E分别为边AB,AC的中点,则四边形BDEC与△ABC的面积之比为( )
A.1:2
B.1:3
C.3:4
D.1:4
3.如图,AD是直角三角形ABC斜边上的中线,AE⊥AD交CB的延长线于E,则图中一定相似的三角形是( )
A.△AED与△ACB
B.△AEB与△ACD
C.△BAE与△ACE
D.△AEC与△DAC
4.如图,在平面直角坐标系中,有点A(6,3),B(6,0),以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1)
B.(2,0)
C.(3,3)
D.(3,1)
5.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.某女模特身高165
cm,下半身长x(cm)与身高l(cm)的比值是0.60.为尽可能达到美的效果,她应穿的高跟鞋的高度大约为( )
A.4
cm
B.6
cm
C.8
cm
D.10
cm
6.如图,为估算某河面的宽度(河两岸平行),在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20
m,CE=10
m,CD=20
m,则河的宽度AB等于( )
A.60
m
B.40
m
C.30
m
D.20
m
7.如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(6,0)
B.(6,3)
C.(6,5)
D.(4,2)
8.如图,在矩形ABCD中,AB=2,BC=3,点E是AD的中点,CF⊥BE于点F,则CF等于( )
A.2
B.2.4
C.2.5
D.2.25
9.如图,在平行四边形ABCD中,E是CD上的一点,DE:EC=2:3,连接AE,BE,BD,且AE,BD交于点F,则S△DEF:S△EBF:S△ABF=( )
A.2:5:25
B.4:9:25
C.2:3:5
D.4:10:25
10.如图,在△ABC中,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论有( )
A.1个
B.2个
C.3个
D.4个
二、填空题(每题5分,共20分)
11.假期,爸爸带小明去A地旅游.小明想知道他所居住的城市与A地之间的距离,他在比例尺为1:500
000的地图上测得所居住的城市距A地32
cm,则小明所居住的城市与A地之间的实际距离为________km.
12.如图,已知点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP,垂足是点B,若在射线BF上找一点M,使以点B,M,C为顶点的三角形与△ABP相似,则BM的长为________.
13.如图,小明把手臂水平向前伸直,手持小尺竖直,瞄准小尺的两端E,F,不断调整站立的位置,使其站立在点D处恰好能看到铁塔的顶部B和底部A,设小明的手臂长l=45
cm,小尺长a=15
cm,点D到铁塔底部A的距离AD=42
m,则铁塔的高度是________m.
14.如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1,再以正△AB1C1的边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2,…,以此类推,则Sn=________.(用含n的式子表示)
三、解答题(15题~18题,每题8分,19,20题,每题10分,21,22题,每题12分,23题14分,共90分)
15.若==≠0,且3x+2y-z=14,求x,y,z的值.
16.如图,在△ABC中,AB=8,BC=4,CA=6,CD∥AB,BD是∠ABC的平分线,BD交AC于点E,求AE的长.
17.如图,在边长为a的正方形ABCD中,M是AD的中点,能否在边AB上找一点N(不与A,B重合),使得△CDM与△MAN相似?若能,请求出AN的长;若不能,请说明理由.
18.如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
(1)求证:△ADE≌△CFE;
(2)若GB=2,BC=4,BD=1,求AB的长.
19.如图,已知在矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,=,△CEF的面积为S1,△AEB的面积为S2,求的值.
20.如图,在边长为1个单位长度的小正方形网格中:
(1)画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1;
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2BC2,请在网格中画出△A2BC2;
(3)求△CC1C2的面积.
21.如图,花丛中有一路灯杆AB.在灯光下,小明在D点处的影长DE=3
m,沿BD方向行走到达G点,DG=5
m,这时小明的影长GH=5
m.如果小明的身高为1.7
m,求路灯杆AB的高度(结果精确到0.1
m).
22.如图,在矩形ABCD中,AB=12
cm,BC=6
cm,点P沿AB边从点A开始向点B以2
cm/s的速度移动,点Q沿DA边从点D开始向点A以1
cm/s的速度移动.如果P,Q同时出发,用t(s)表示移动的时间(0≤t≤6),那么:
(1)当t为何值时,△QAP是等腰直角三角形?
(2)根据四边形QAPC的面积的计算结果,能得出什么结论?
(3)当t为何值时,以点Q,A,P为顶点的三角形与△ABC相似?
23.如图①,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE.
将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)当α=0°和α=180°时,求的值.
(2)试判断当0°≤α<360°时,的值有无变化?请仅就图②的情况给出证明.
(3)当△EDC旋转至A,D,E三点共线时,求线段BD的长.
答案
一、1.B 2.C 3.C 4.A 5.C
6.B 点拨:∵AB⊥BC,CD⊥BC,∴∠ABE=∠DCE=90°.
又∵∠AEB=∠DEC,
∴△ABE∽△DCE.
∴=,即=.
∴AB=40
m.
7.B
8.B 点拨:由∠A=∠ABC=90°,CF⊥BE,易证△ABE∽△FCB.
∴=.由AE=×3=1.5,
AB=2,易得BE=2.5,
∴=.∴CF=2.4.
9.D
10.D 点拨:∵四边形ADEF为正方形,∴∠FAD=90°,AD=AF=EF,
∴∠CAD+∠FAG=90°.
∵FG⊥CA,
∴∠G=90°=∠ACB.
∴∠AFG+∠FAG=90°.
∴∠DAC=∠AFG.
在△FGA和△ACD中,
∴△FGA≌△ACD(AAS).
∴AC=FG.故①正确.
∵BC=AC,
∴FG=BC.
∵∠ACB=90°,FG⊥CA,
∴FG∥BC.
∴四边形CBFG是矩形.
∴∠CBF=90°,S△FAB=FB·FG=S四边形CBFG.故②正确.
∵CA=CB,∠C=∠CBF=90°,
∴∠ABC=∠ABF=45°.故③正确.
易知∠FQE=∠DQB=∠ADC,∠E=∠C=90°,
∴△ACD∽△FEQ,
∴AC∶AD=FE∶FQ.
∴AD·FE=AD2=FQ·AC.故④正确.
二、11.160 点拨:设小明所居住的城市与A地之间的实际距离为x
km,根据题意可列比例式为=,解得x=160.
12.或3 点拨:由题意得∠ABC=∠FBP=90°,∴∠ABP=∠CBF.当△MBC∽△ABP时,BM:AB=BC:BP,得BM=4×4÷3=;当△CBM∽△ABP时,BM:BP=CB:AB,得BM=4×3÷4=3.
13.14 点拨:过点C作CH⊥AB于点H,交EF于点P,如图,则CH=DA=42
m,由题意知,CP=45
cm=0.45
m,EF=15
cm=0.15
m.
∵EF∥AB,
∴∠CEF=∠CBA,∠CFE=∠CAB.
∴△CEF∽△CBA.
∴=,即=.
∴AB=14
m,即铁塔的高度是14
m.
14.× 点拨:在正△ABC中,AB1⊥BC,∴BB1=BC=1.在Rt△ABB1中,AB1===,
根据题意可得△AB2B1∽△AB1B,记△AB1B的面积为S,∴=.∴S1=S.
同理可得S2=S1,S3=S2,S4=S3,…,Sn=Sn-1.
又∵S=×1×=,
∴S1=S=×,S2=S1=×,
S3=S2=×,
S4=S3=×,
…,
Sn=×.
三、15.解:设===k(k≠0),
则x=2k,y=3k,z=5k,
∵3x+2y-z=14,
∴6k+6k-5k=14,解得k=2,
∴x=4,y=6,z=10.
16.解:∵BD是∠ABC的平分线,
∴∠ABD=∠CBD,
∵AB∥CD,∴∠D=∠ABD,
∴∠D=∠CBD,∴BC=CD,
∵BC=4,∴CD=4,
又∵∠AEB=∠CED,
∴△ABE∽△CDE,
∴=,∴=,
∴AE=2CE,∵AC=6=AE+CE,
∴AE=4.
17.解:分两种情况讨论:
(1)若△CDM∽△MAN,则=.
∵正方形ABCD的边长为a,M是AD的中点,∴AN=a.
(2)若△CDM∽△NAM,则=.∵正方形ABCD的边长为a,M是AD的中点,∴AN=a,即N点与B点重合,不符合题意.
∴能在边AB上找一点N(不与A,B重合),使得△CDM与△MAN相似,此时AN=a.
18.(1)证明:∵AB∥FC,
∴∠A=∠ECF.
又∵∠AED=∠CEF,
且DE=FE,
∴△ADE≌△CFE(AAS).
(2)解:方法一 ∵AB∥FC,
∴∠GBD=∠GCF,∠GDB=∠F.
∴△GBD∽△GCF.
∴=.
∴=.
∴CF=3.
由(1)得△ADE≌△CFE,
∴AD=CF=3.
∴AB=AD+BD=3+1=4.
方法二 如图,取BC的中点H,连接EH.
∵△ADE≌△CFE,∴AE=CE.
∴EH是△ABC的中位线.
∴EH∥AB,且EH=AB.
∴∠GBD=∠GHE,∠GDB=∠GEH.∴△GBD∽△GHE.
∴=.∴=.
∴EH=2.∴AB=2EH=4.
19.解:∵BF⊥AC,
∴∠ACB+∠CBF=90°,
∵四边形ABCD为矩形,
∴∠BCF=∠ABC=90°,AB∥CD,AD=BC.
∴∠CAB+∠ACB=90°.∴∠CAB=∠CBF.
∴△FCB∽△CBA.∴CF:CB=CB:AB,
又∵=,
∴CF:CB=CB:AB=AD:AB=1:2.
∴FC:AB=1:4.
∵FC∥AB,∴△FCE∽△BAE.
∴===.
20.解:(1)如图所示.
(2)如图所示.
(3)如图,△CC1C2的面积为×3×6=9.
21.解:根据题意得AB⊥BH,CD⊥BH,FG⊥BH.
在Rt△ABE和Rt△CDE中,
∵AB⊥BH,CD⊥BH,∴CD∥AB,
可证得△CDE∽△ABE.
∴=
,①
同理得=,②
又∵CD=FG=1.7
m,
由①②可得
=,
即=,
解之得BD=7.5
m,
将BD=7.5
m代入①得
AB=5.95
m≈6.0
m.
故路灯杆AB的高度约为6.0
m.
22.解:(1)由题意知AP=2t,DQ=t,QA=6-t,当QA=AP时,
△QAP是等腰直角三角形,
∴6-t=2t,解得t=2.
∴当t=2时,△QAP是等腰直角三角形.
(2)四边形QAPC的面积=S△QAC+S△APC=AQ·AB+AP·BC=(36-6t)+6t=36.由计算结果发现:在P,Q两点移动的过程中,四边形QAPC的面积始终保持不变.
(3)分两种情况:
①当=时,△QAP∽△ABC,则=,即t=1.2;
②当=时,△PAQ∽△ABC,则=,即t=3.
∴当t=1.2或t=3时,以点Q,A,P为顶点的三角形与△ABC相似.
23.解:(1)当α=0°时,∵BC=2AB=8,∴AB=4.∵点D,E分别是边BC,AC的中点,∴BD=4,AE=EC=AC.∵∠B=90°,
∴AC==4
,
∴AE=CE=2
,
∴==.
当α=180°时,如图①,
易得AC=4
,CE=2
,CD=4,
∴===.
(2)无变化.
证明:在题图①中,∵DE是△ABC的中位线,
∴DE∥AB,
∴=,∠EDC=∠B=90°.
如题图②,∵△EDC在旋转过程中的形状和大小不变,
∴=仍然成立.
又∵∠ACE=∠BCD=α,
∴△ACE∽△BCD.∴=.
在Rt△ABC中,AC===4
.
∴==.∴=.
∴的值无变化.
(3)当△EDC在BC的上方,且A,D,E三点共线时,四边形ABCD为矩形,如图②,∴BD=AC=4
;当△EDC在BC的下方,且A,E,D三点共线时,△ADC为直角三角形,如图③,由勾股定理可得AD==8.又易知DE=2,
∴AE=6.∵=,∴BD=.
综上,BD的长为4
或.
