五年级下册数学课件-2.3.3 质数和合数练习四-人教版(共26张PPT)
文档属性
| 名称 | 五年级下册数学课件-2.3.3 质数和合数练习四-人教版(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-02 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
null
2.3.3
练习四
五
下
数
学
1
2
3
4
温故知新
新知探究
课堂练习
课堂小结
目
录
CONTENTS
温故知新
学而时习之,不亦说乎
03
1
一个数只有1和它本身两个因数,这个数叫作质数。
一个数除了1和它本身以外还有别的因数,这个数叫作合数。
既不是质数也不是是合数
5的倍数
2的倍数
个位上是0、2、4、6、8的数,都是2的倍数。
个位上是0或5的数,都是5的倍数。
3的倍数
各位上数的和是3的倍数,这个数就是3的倍数。
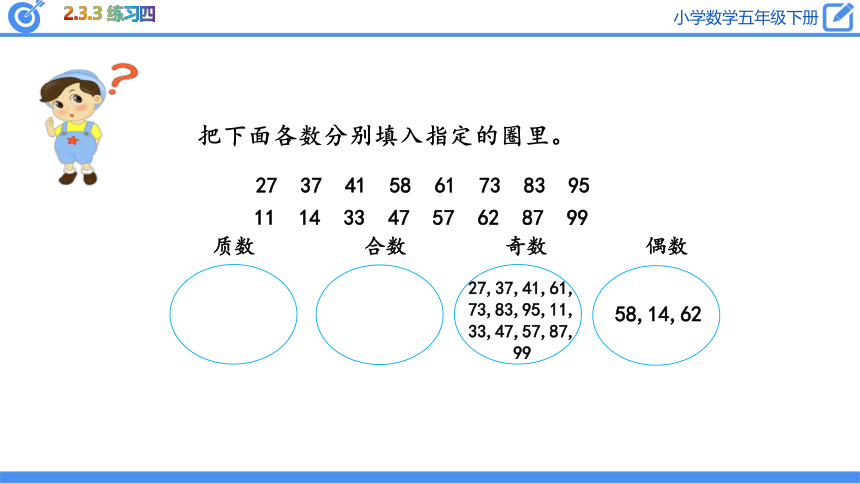
质数
合数
奇数
偶数
27,37,41,61,73,83,95,11,33,47,57,87,99
58,14,62
37
41
58
61
73
83
95
11
14
33
47
57
62
87
99
奇数×偶数=偶数
奇数×奇数=奇数
偶数×偶数=偶数
奇数±偶数=奇数
奇数±奇数=偶数
偶数±偶数=偶数
课堂练习
纸上得来终觉浅,绝知此事要躬行
03
3
在1~20中,
奇数有(
);偶数有(
);质数有(
);
合数有(
)。
1,3,5,7,9,11,13,15,17,19
2,4,6,8,10,12,14,16,18,20
2,3,5,7,11,13,17,19
4,6,8,9,10,12,14,15,16,18,20
×
2
15
9
对于概念含混不清。合数不一定都是偶数,同样质数也不一定都是奇数。
判断:两个质数的和是偶数。
(
)
×
举一个简单的反例即可。比如2+3=5,2和3都是质数,而它们的和5是奇数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
在( )里填上合适的质数。
14=( )+( )
8=( )+( )
12=( )+( )
14=( )×( )
30=( )+( )
10=( )+( )
3
11
3
5
5
7
2
7
13
17
3
7
质数:2,3,5,7,11,13,17,23,29……
答案不唯一。想想还能怎么填?
两个质数的和是小于100的奇数,并且是13的倍数。这两个质数可能是多少?
13的倍数
13×1=13
13×2=26
13×3=39
13×4=52
13×5=65
13×6=78
13×7=91
……
把13、39、65、91写成两个质数相加。
13=2+11
39=2+37
91=2+89
答:这两个质数可能是2和11、2和37、2和89。
65不能写成两个质数相加。
我们两个的和是6,积是8。
2+4=6
2×4=8
2
4
我们两个的和是10,积是21。
3+7=10
3×7=21
3
7
13+7=20
13×7=91
13
7
西岸
东岸
1
2
3
4
5
6
(1)第5次东岸,第10次西岸,第115次东岸。
(2)奇数次从东岸出发,偶数次从西岸出发。
一只小船每天在河的东西两岸运送乘客,从东岸到西岸或从西岸到东岸都算一次。
(1)一天,这只小船从东岸开始运送乘客,第5次从东岸出发还是从西岸出发?第10次和第115次呢?(2)你发现了什么规律?
偶数
用两个质数相加的形式表示
4
4=2+2
6
6=3+3
8
8=5+3
10
10=7+3
12
12=7+5
14
14=7+7
……
……
是不是所有大于2的偶数,都可以表示为两个质数的和呢?
你知道吗?
哥德巴赫猜想
这个问题是德国数学家哥德巴赫最先提出的,所以被称作哥德巴赫猜想。世界各国的数学家都想攻克这一难题,但至今还未解决。我国数学家陈景润在这一领域取得了举世瞩目的成果。哥德巴赫猜想看似简单,要证明却非常困难,成为数学中一个著名的难题,被称为“数学皇冠上的明珠”。
哥德巴赫
课堂小结
学而不思则惘,思而不学则殆
03
4
1.根据2、3、5的倍数特征解决问题
2.根据奇数、偶数、质数、合数的
定义解决问题
知识小结
学如蜜蜂采蜜,采过许多花,才能酿出许多蜜。
null
讲师:文小语
null
2.3.3
练习四
五
下
数
学
1
2
3
4
温故知新
新知探究
课堂练习
课堂小结
目
录
CONTENTS
温故知新
学而时习之,不亦说乎
03
1
一个数只有1和它本身两个因数,这个数叫作质数。
一个数除了1和它本身以外还有别的因数,这个数叫作合数。
既不是质数也不是是合数
5的倍数
2的倍数
个位上是0、2、4、6、8的数,都是2的倍数。
个位上是0或5的数,都是5的倍数。
3的倍数
各位上数的和是3的倍数,这个数就是3的倍数。
质数
合数
奇数
偶数
27,37,41,61,73,83,95,11,33,47,57,87,99
58,14,62
37
41
58
61
73
83
95
11
14
33
47
57
62
87
99
奇数×偶数=偶数
奇数×奇数=奇数
偶数×偶数=偶数
奇数±偶数=奇数
奇数±奇数=偶数
偶数±偶数=偶数
课堂练习
纸上得来终觉浅,绝知此事要躬行
03
3
在1~20中,
奇数有(
);偶数有(
);质数有(
);
合数有(
)。
1,3,5,7,9,11,13,15,17,19
2,4,6,8,10,12,14,16,18,20
2,3,5,7,11,13,17,19
4,6,8,9,10,12,14,15,16,18,20
×
2
15
9
对于概念含混不清。合数不一定都是偶数,同样质数也不一定都是奇数。
判断:两个质数的和是偶数。
(
)
×
举一个简单的反例即可。比如2+3=5,2和3都是质数,而它们的和5是奇数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
在( )里填上合适的质数。
14=( )+( )
8=( )+( )
12=( )+( )
14=( )×( )
30=( )+( )
10=( )+( )
3
11
3
5
5
7
2
7
13
17
3
7
质数:2,3,5,7,11,13,17,23,29……
答案不唯一。想想还能怎么填?
两个质数的和是小于100的奇数,并且是13的倍数。这两个质数可能是多少?
13的倍数
13×1=13
13×2=26
13×3=39
13×4=52
13×5=65
13×6=78
13×7=91
……
把13、39、65、91写成两个质数相加。
13=2+11
39=2+37
91=2+89
答:这两个质数可能是2和11、2和37、2和89。
65不能写成两个质数相加。
我们两个的和是6,积是8。
2+4=6
2×4=8
2
4
我们两个的和是10,积是21。
3+7=10
3×7=21
3
7
13+7=20
13×7=91
13
7
西岸
东岸
1
2
3
4
5
6
(1)第5次东岸,第10次西岸,第115次东岸。
(2)奇数次从东岸出发,偶数次从西岸出发。
一只小船每天在河的东西两岸运送乘客,从东岸到西岸或从西岸到东岸都算一次。
(1)一天,这只小船从东岸开始运送乘客,第5次从东岸出发还是从西岸出发?第10次和第115次呢?(2)你发现了什么规律?
偶数
用两个质数相加的形式表示
4
4=2+2
6
6=3+3
8
8=5+3
10
10=7+3
12
12=7+5
14
14=7+7
……
……
是不是所有大于2的偶数,都可以表示为两个质数的和呢?
你知道吗?
哥德巴赫猜想
这个问题是德国数学家哥德巴赫最先提出的,所以被称作哥德巴赫猜想。世界各国的数学家都想攻克这一难题,但至今还未解决。我国数学家陈景润在这一领域取得了举世瞩目的成果。哥德巴赫猜想看似简单,要证明却非常困难,成为数学中一个著名的难题,被称为“数学皇冠上的明珠”。
哥德巴赫
课堂小结
学而不思则惘,思而不学则殆
03
4
1.根据2、3、5的倍数特征解决问题
2.根据奇数、偶数、质数、合数的
定义解决问题
知识小结
学如蜜蜂采蜜,采过许多花,才能酿出许多蜜。
null
讲师:文小语
