人教版高二物理必修二第一章曲线运动(共69张PPT)
文档属性
| 名称 | 人教版高二物理必修二第一章曲线运动(共69张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-06-03 08:07:27 | ||
图片预览









文档简介
(共70张PPT)
让带有水的雨伞绕着伞柄转动,水滴沿伞边圆周的切线飞出.
(1)方向:任何做曲线运动的物体,沿曲线运动时,其速度方向必然是时刻改变的。物体在某点的即时速度方向,就是曲线在该点的切线方向
因为速度是矢量,有大小、也有方向,只要大小和方向中有一个改变了,就是速度变了,也就是有加速度。所以,曲线运动是速度方向时刻改变的变速运动。
(2)曲线运动的性质
思考:曲线运动为什么一定是变速运动?
(3)曲线运动的分类
加速度(合外力)恒定的曲线运动为匀变速曲线运动;加速度(合外力)变化的曲线运动为非匀变速曲线运动。
(4)曲线运动的条件
当运动物体所受合力的方向跟它的速度方向不在同一直线上时,物体就做曲线运动。
解释
当F合与V同向,据牛顿第二定律,产生的a的方向与V的方向同向,物体就做直线运动。当它们不在一直线上,产生的a的方向与V的方向成一角度,合力不但可以改变V的大小,还可以改变V的方向,物体就做曲线运动。
思考:V0=0且受恒力作用时,能做曲线运动吗?
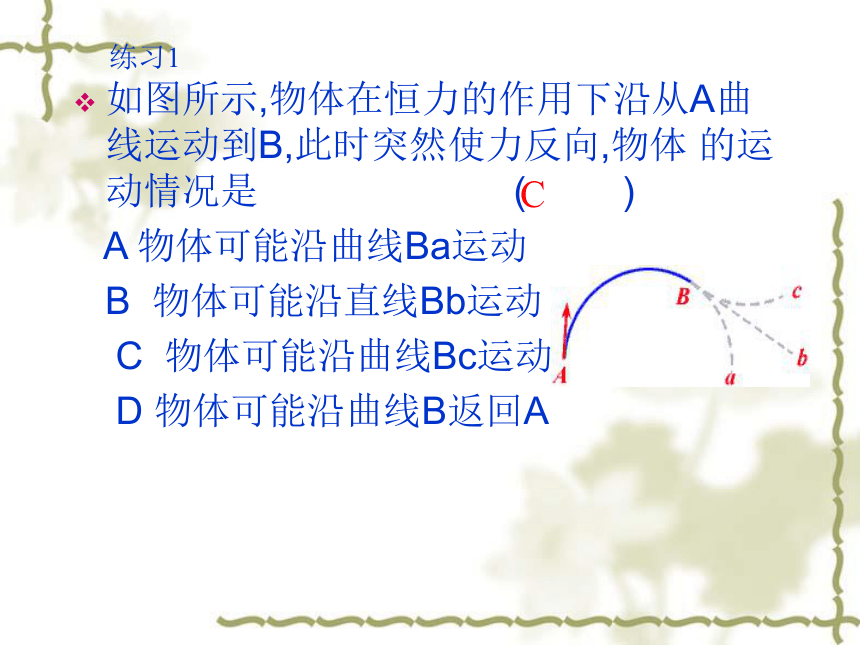
如图所示,物体在恒力的作用下沿从A曲线运动到B,此时突然使力反向,物体
的运动情况是
(
)
A
物体可能沿曲线Ba运动
B
物体可能沿直线Bb运动
C
物体可能沿曲线Bc运动
D
物体可能沿曲线B返回A
C
练习1
练习题2
下列关于力和运动的说法中正确的是(
)
A.
物体在恒力作用下不可能做曲线运动
B.物体在变力作用下不可能做直线运动
C.物体在变力作用下不可能做曲线运动
D.物体在变力作用下可能做曲线运动
D
练习题3
3、某物体受同一平面内的几个力作用而做匀速直线运动,从某时刻起撤去其中一个力,而其它力没变,则该物体(
)
A、一定做匀加速直线运动
B、一定做匀减速直线运动
C、其轨迹可能是曲线
D、其轨迹不可能是直线
C
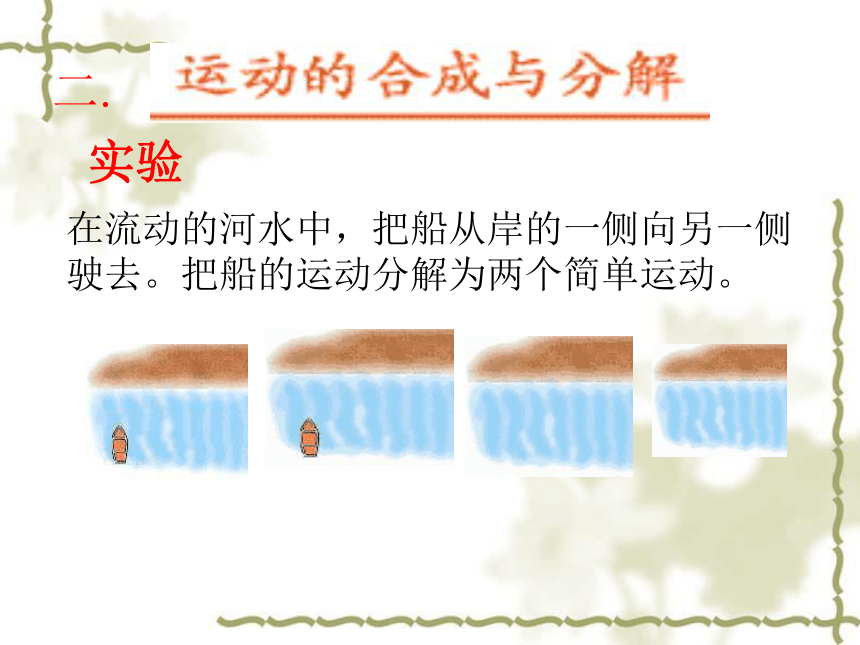
二.
实验
在流动的河水中,把船从岸的一侧向另一侧驶去。把船的运动分解为两个简单运动。
一.几个基本概念
1.合运动:物体实际发生的运动叫合运动.
2分运动:物体实际运动可以看作物体同时参与了几个分运动,这几个运动就是物体实际运动的分运动.
3运动的合成:已知分运动求合运动
4运动的分解:已知合运动求分运动.
二.合运动与分运动的特点
1合位移与分位移,合速度与分速度,合加速度与分加速度都遵循平行四边形定则.
2合运动的时间与分运动的时间相等.
3物体实际发生的运动才是合运动
曲线运动——运动的合成与分解
机械运动可以划分为平动和转动,而平动又可以划分为直线运动和曲线运动,所以曲线运动属于平动形式,做曲线运动的物体仍然可以看成一个质点,曲线运动比直线运动更为普遍。例如,车辆拐弯;月球绕地球约27天转一圈;地球绕太阳约一年转一周;太阳绕银河系中心约2.2亿年转一周。
问题1:绳拉小球在光滑的水平面上做圆周运动,当绳断后小球将沿什么方向运动?
现象:沿切线方向飞出
原因:绳断后小球速度方向不再发生变化,由于惯性,从即刻起小球做匀速直线运动,沿切线飞出。
演示实验:砂轮磨刀使火星沿切线飞出
让撑开的带有雨滴的雨伞旋转,雨滴沿伞边切线方向飞出。
总结:曲线运动中,速度方向是时刻改变的,在某时刻的即时速度方向在曲线的这一点的切线方向上。曲线运动一定是变速运动
问题2:如果合外力与速度在同一直线上,物体将做什么样的运动?
变速直线运动
问题3:绳拉小球在光滑水平面上做速度大小不变的圆周运动,绳子的拉力T起什么作用?
改变速度方向
曲线运动的条件:
合外力与速度不在同一直线上时,物体做曲线运动。
运动的合成与分解实例分析
(1)船渡河问题分析
A、v船>v水
B、v船B
曲线运动
方向:切线方向
运动性质:变速运动
条件
--物体所受合外力与速度不在同一直线上
研究方法
运动的合成与分解
平行四边形定则
运动的等时性,独立性
平抛
条件:只受重力
有水平初速度
规律:
水平方向:匀速直线运动
竖直方向:自由落体运动
飞行时间:只取决于高度
运动性质:匀变速运动
条件:只受重力
有竖直初速度
规律:
竖直方向:匀速运动和自由落体运动
运动性质:匀变速运动
直线运动
竖直下抛运动
竖直上抛运动
斜抛
抛体运动
条件:只受重力;
有斜向上的初速度
规律:
水平方向:匀速直线运动
竖直方向:竖直上抛运动
运动性质:匀变速运动
第一章
抛体运动复习
初速为零的匀加速直线运动
斜抛运动
匀变速曲线运动
其它夹角
平抛运动
匀变速曲线运动
与F垂直
竖直上抛运动
匀减速直线运动
与F反向
竖直下抛运动
匀加速直线运动
与F同向
不为零
自由落体运动
零
恒力(F)
大小不为零
匀速直线运动
不为零
静止
零
大小为零
特例
运动特点
初速度
合外力情况
第一章
抛体运动复习
把物体以一定的初速度沿竖直方向向下抛出,仅在重力的作用下物体所作的运动叫做竖直下抛运动.
把物体以一定的初速度沿竖直方向向上抛出,仅在重力的作用下物体所作的运动叫做竖直上抛运动.
竖直上抛运动和竖直下抛运动都是匀变速直线运动,匀变直线运动的所有公式在这里都能使用,但要注意初速度和加速度的方向.
第一章
抛体运动复习
①曲线运动一定是变速运动,速度方向一定会发生变化,但大小不一定变化。
②不在同一直线上的两个直线运动,如果两个运动都是匀速直线运动,则合运动一定是直线运动;如果一个是匀速直线运动,一个是变速直线运动,则合运动一定是曲线运动。
③曲线运动可能受恒力,也可能受变力
④平抛运动是匀变速运动。
第一章
抛体运动复习
研究运动的合成与分解,目的在于把一些复杂的运动简化为比较简单的直线运动。
运动合成与分解的内容:位移、速度、加速度。
运动合成与分解的方法——平行四边形定则。
运动的合成与分解的解题要点:
1.在实际解题时,经常用到平行四边形定则,应注意掌握
2.认真分析谁是合运动、谁是分运动。
(一般说来,能够观察到(真实)的运动是合运动)
3.要注意寻求分运动效果。
4.合运动与分运动具有:等时性、独立性、等效性。
5.分析此类问题的一般方法:运动合成分解法、微元法。
第一章
抛体运动复习
【方法提示】
根据运动效果认真做好运动矢量图,是解题的关键。
【问题综述】
V1为水流速度,V2为船相对于静水的速度,θ为V1与V2的夹角,L为河宽。
沿水流方向:速度为V∥=V1+V2cosθ的匀速直线运动
垂直河岸方向:速度为V⊥=V2sinθ的匀速直线运动(渡河)
①欲使船垂直渡河,V∥=0
②欲使船垂直渡河时间最短,θ=900
第一章
抛体运动复习
【答案】①θ=600
②垂直于河岸
运动矢量分析
【例题】一船准备渡河,已知水流速度为V0=1m/s,船在
静水中的航速为V’=2m/s,则:
①要使船能够垂直地渡过河去,那么应向何方划船?
②要使船能在最短时间内渡河,应向何方划船?
第一章
抛体运动复习
运动矢量分析
【答案】
Vmin=2.4m/s
【例题】一人横渡40米宽的河,河水流速3
m/s,下游距下水30米处有一拦河坝,为保证安全渡河,此人相对于水的速度至少为多少?
第一章
抛体运动复习
运动矢量分析
【答案】θ=600
Vmin≈173m
【例题】小孩游泳的速度是河水流速的二分之一,河宽d=100m,问小孩向什么方向游向对岸,才能使他被河水冲行的距离最短?这最短的距离是多少?
第一章
抛体运动复习
【问题综述】
此类问题的关键是:
1.准确判断谁是合运动,谁是分运动;实际运动是合运动
2.根据运动效果寻找分运动;
3.一般情况下,分运动表现在:
①沿绳方向的伸长或收缩运动;
②垂直于绳方向的旋转运动。
4.根据运动效果认真做好运动矢量图,是解题的关键
5.对多个用绳连接的物体系统,要牢记在绳的方向上
的速度大小相等。
6.此类问题还经常用到微元法求解。
第一章
抛体运动复习
【答案】
寻找分运动效果
减速
【例题】如图所示,纤绳以恒定速率V
沿水平方向通过定滑轮牵引小船靠岸,当纤绳与水面夹角为θ时,船靠岸的速度是
,若使船匀速靠岸,则纤绳的速度是
。(填:匀速、加速、减速)
第一章
抛体运动复习
【例题】如图所示,汽车沿水平路面以恒定速度v前进,则当拉绳与水平方向成θ角时,被吊起的物体M
的速度为vM=
。
【答案】
寻找分运动效果
VM=V·cosθ
第一章
抛体运动复习
竖直上抛运动的处理方法
由于竖直上抛运动涉及上升和下降两个过程,因此在处理竖直上抛运动问题时,常有以下两种思路:
⑴分步处理
①上升过程当作匀减速直线运动
②下降过程当作匀加速直线运动(自由落体运动)
⑵整体处理
就整体而言,竖直上抛运动是一种匀变速直线运动,加速度为g,解题中注意各物理量的符号。
在实际问题中。选取哪种方法进行处理,应视问题的方便而定。
第一章
抛体运动复习
竖直上抛运动的规律:
解题时,认真作出矢量图,注意物理量的方向。
1.平抛运动(常规)分解为:
①水平方向的匀速直线运动;
②竖直方向的自由落体运动。
2.斜抛运动(常规)分解为:
①水平方向的匀速直线运动;
②竖直方向的竖直上抛运动。
第一章
抛体运动复习
第一章
抛体运动复习
做平抛运动的物体落在斜面上
物体从斜面上平抛又落回到斜面
可得知两分速度与斜面间的夹角。
可得知两分位移间的几何关系。
当合速度平行于斜面时,物体离斜面最远。
以v0的水平初速度抛出一物体,飞行一段时间后,垂直地撞在倾角为a的斜面上,则物体飞行的时间是多少?
第一章
抛体运动复习
实验的注意事项
每次小球均从同一高度下落
斜槽末端水平
数据处理
根据各点间的水平距离判定时间间隔
根据相同时间间隔内竖直位移关系判断图中第一点是否是平抛运动的起点
第一章
抛体运动复习
研究运动的合成与分解:目的在于把一些复杂的运动简化为比较简单的直线运动。
运动合成与分解的内容:位移、速度、加速度。
运动合成与分解的方法——平行四边形定则。
绳子拉物体一般情况下,分运动表现在:
①沿绳方向的伸长或收缩运动;
②垂直于绳方向的旋转运动
第一章
抛体运动复习
研究抛体运动时:通常是将一个复杂的运动分解成两个相互垂直直线运动。如:平抛运动——分解为水平方向的匀速直线运动和竖直方向的自由落体运动;又如:斜抛运动——分解为水平方向的匀速直线运动的竖直方向的竖直上抛运动。
o
x
y
A
平抛运动
水平坐标:x=v0t
竖直坐标:y=gt2/2
速度公式:
Vx=Vo
Vy=gt
第一章
抛体运动复习
运动中的“微元法”实质是:
在运动的过程中,选取一微小时间△t,在此时间内,运动物体发生一微小位移,然后利用数学极限思想,对运动进行分析。
由于运动时间极短,所以不论物体做何种运动,都可看成做匀速直线运动。
这种方法由于涉及高深数学理论,所以在高中并不常用。但它却是解决连续变化物理量的求解的最基础、最适用的方法。
第一章
抛体运动复习
例1:船在静水中的速度v1=4m/s,河水速度v2=3m/s,河宽200m
求(1)船以最短时间过河,船头向何方开去,所用时间多少?
(2)船以最短位移过河,船头向何方开去,所用时间多少,速度多大?
解:(1)船头总是垂直河岸过河,所以时间最短:t=s/v1=50s
(2)船以最短位移过河,合位移垂直河岸v=√7
m/s
船头与河岸成α角向上游开去tanα
=√7
/3
时间:t=s/v=200/√7
例2
一艘小船在
200m宽的河中横渡到对岸,已知水流速度是2m/s,小船在静水中的速度是4m/s,求:
①当船头始终正对着对岸时,小船多长时间到达对岸,小船实际运行了多远?
②如果小船的路径要与河岸垂直,应如何行驶?消耗的时间是多少?
③如果小船要用最短时间过河,应如何?船行最短时间为多少??
简答:
①在解答本题的时候可由此提问:船头始终正对河岸代表什么含义.(①题的答案:50秒,下游100米)
②路径与河岸垂直——船的实际运动——船的合运动(在两个分运动的中间,并与河岸垂直)(②题的答案:与上游河岸成60°,57.7s)
③分析本题,可以得到求t最小的方法:
1、河宽一定,要想使时间最少应使垂直河岸方向的分速度最大,即正对河岸航行,则
2、或者由
三个式子一一分析
一定,
又有最小值,即河宽,便可以求出渡河最短时间.
(③题的答案:50s)
例3
在高处拉低处小船时,通常在河岸上通过滑轮用钢绳拴船,若拉绳的速度为4m/s,当拴船的绳与水平方向成60°时,船的速度是多少?(8m/s)
?????????????????????????????????????????????????????????????????????????????????????????????????????
上题提示:(提示:在分析船的运动时,我们发现船的运动产生了两个运动效果:绳子在不断缩短;而且绳子与河岸的夹角不断减小,所以我们可以将船的运动——实际运动——合运动分解成沿绳子方向的运动和垂直绳子方向所做的圆周运动)
1、船沿水平方向前进——此方向为合运动,求合速度v.
2、小船的运动可以看成为沿绳子缩短方向的运动和垂直绳子方向做圆周运动的合运动.
1、关于运动的合成与分解的说法中,正确的是(??
)
A、合运动的位移为分运动的位移的矢量和.
B、合运动的速度一定比其中一个分速度大.
C、合运动的时间为分运动时间之和.
D、合运动的时间与各分运动时间相等
AD
让带有水的雨伞绕着伞柄转动,水滴沿伞边圆周的切线飞出.
(1)方向:任何做曲线运动的物体,沿曲线运动时,其速度方向必然是时刻改变的。物体在某点的即时速度方向,就是曲线在该点的切线方向
因为速度是矢量,有大小、也有方向,只要大小和方向中有一个改变了,就是速度变了,也就是有加速度。所以,曲线运动是速度方向时刻改变的变速运动。
(2)曲线运动的性质
思考:曲线运动为什么一定是变速运动?
(3)曲线运动的分类
加速度(合外力)恒定的曲线运动为匀变速曲线运动;加速度(合外力)变化的曲线运动为非匀变速曲线运动。
(4)曲线运动的条件
当运动物体所受合力的方向跟它的速度方向不在同一直线上时,物体就做曲线运动。
解释
当F合与V同向,据牛顿第二定律,产生的a的方向与V的方向同向,物体就做直线运动。当它们不在一直线上,产生的a的方向与V的方向成一角度,合力不但可以改变V的大小,还可以改变V的方向,物体就做曲线运动。
思考:V0=0且受恒力作用时,能做曲线运动吗?
如图所示,物体在恒力的作用下沿从A曲线运动到B,此时突然使力反向,物体
的运动情况是
(
)
A
物体可能沿曲线Ba运动
B
物体可能沿直线Bb运动
C
物体可能沿曲线Bc运动
D
物体可能沿曲线B返回A
C
练习1
练习题2
下列关于力和运动的说法中正确的是(
)
A.
物体在恒力作用下不可能做曲线运动
B.物体在变力作用下不可能做直线运动
C.物体在变力作用下不可能做曲线运动
D.物体在变力作用下可能做曲线运动
D
练习题3
3、某物体受同一平面内的几个力作用而做匀速直线运动,从某时刻起撤去其中一个力,而其它力没变,则该物体(
)
A、一定做匀加速直线运动
B、一定做匀减速直线运动
C、其轨迹可能是曲线
D、其轨迹不可能是直线
C
二.
实验
在流动的河水中,把船从岸的一侧向另一侧驶去。把船的运动分解为两个简单运动。
一.几个基本概念
1.合运动:物体实际发生的运动叫合运动.
2分运动:物体实际运动可以看作物体同时参与了几个分运动,这几个运动就是物体实际运动的分运动.
3运动的合成:已知分运动求合运动
4运动的分解:已知合运动求分运动.
二.合运动与分运动的特点
1合位移与分位移,合速度与分速度,合加速度与分加速度都遵循平行四边形定则.
2合运动的时间与分运动的时间相等.
3物体实际发生的运动才是合运动
曲线运动——运动的合成与分解
机械运动可以划分为平动和转动,而平动又可以划分为直线运动和曲线运动,所以曲线运动属于平动形式,做曲线运动的物体仍然可以看成一个质点,曲线运动比直线运动更为普遍。例如,车辆拐弯;月球绕地球约27天转一圈;地球绕太阳约一年转一周;太阳绕银河系中心约2.2亿年转一周。
问题1:绳拉小球在光滑的水平面上做圆周运动,当绳断后小球将沿什么方向运动?
现象:沿切线方向飞出
原因:绳断后小球速度方向不再发生变化,由于惯性,从即刻起小球做匀速直线运动,沿切线飞出。
演示实验:砂轮磨刀使火星沿切线飞出
让撑开的带有雨滴的雨伞旋转,雨滴沿伞边切线方向飞出。
总结:曲线运动中,速度方向是时刻改变的,在某时刻的即时速度方向在曲线的这一点的切线方向上。曲线运动一定是变速运动
问题2:如果合外力与速度在同一直线上,物体将做什么样的运动?
变速直线运动
问题3:绳拉小球在光滑水平面上做速度大小不变的圆周运动,绳子的拉力T起什么作用?
改变速度方向
曲线运动的条件:
合外力与速度不在同一直线上时,物体做曲线运动。
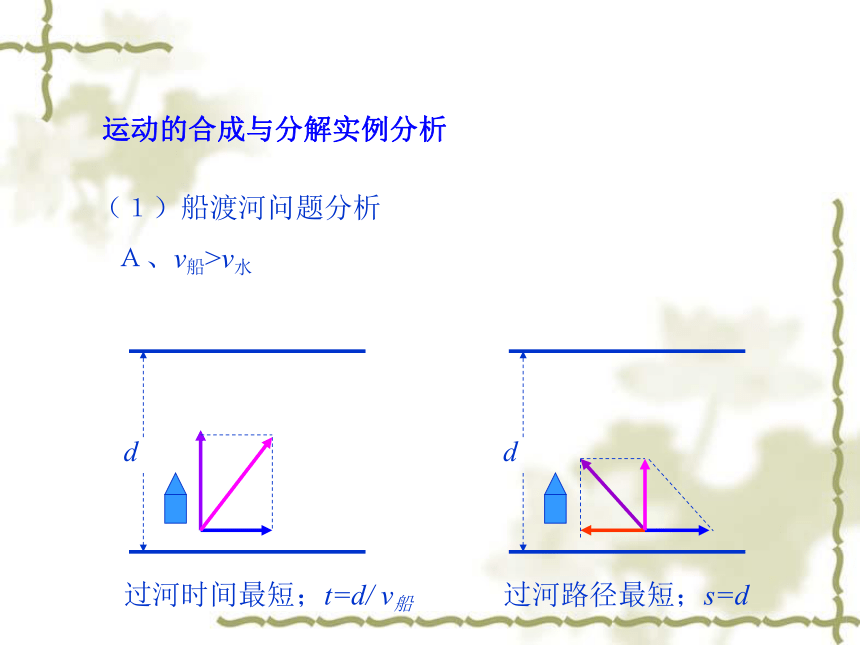
运动的合成与分解实例分析
(1)船渡河问题分析
A、v船>v水
B、v船
曲线运动
方向:切线方向
运动性质:变速运动
条件
--物体所受合外力与速度不在同一直线上
研究方法
运动的合成与分解
平行四边形定则
运动的等时性,独立性
平抛
条件:只受重力
有水平初速度
规律:
水平方向:匀速直线运动
竖直方向:自由落体运动
飞行时间:只取决于高度
运动性质:匀变速运动
条件:只受重力
有竖直初速度
规律:
竖直方向:匀速运动和自由落体运动
运动性质:匀变速运动
直线运动
竖直下抛运动
竖直上抛运动
斜抛
抛体运动
条件:只受重力;
有斜向上的初速度
规律:
水平方向:匀速直线运动
竖直方向:竖直上抛运动
运动性质:匀变速运动
第一章
抛体运动复习
初速为零的匀加速直线运动
斜抛运动
匀变速曲线运动
其它夹角
平抛运动
匀变速曲线运动
与F垂直
竖直上抛运动
匀减速直线运动
与F反向
竖直下抛运动
匀加速直线运动
与F同向
不为零
自由落体运动
零
恒力(F)
大小不为零
匀速直线运动
不为零
静止
零
大小为零
特例
运动特点
初速度
合外力情况
第一章
抛体运动复习
把物体以一定的初速度沿竖直方向向下抛出,仅在重力的作用下物体所作的运动叫做竖直下抛运动.
把物体以一定的初速度沿竖直方向向上抛出,仅在重力的作用下物体所作的运动叫做竖直上抛运动.
竖直上抛运动和竖直下抛运动都是匀变速直线运动,匀变直线运动的所有公式在这里都能使用,但要注意初速度和加速度的方向.
第一章
抛体运动复习
①曲线运动一定是变速运动,速度方向一定会发生变化,但大小不一定变化。
②不在同一直线上的两个直线运动,如果两个运动都是匀速直线运动,则合运动一定是直线运动;如果一个是匀速直线运动,一个是变速直线运动,则合运动一定是曲线运动。
③曲线运动可能受恒力,也可能受变力
④平抛运动是匀变速运动。
第一章
抛体运动复习
研究运动的合成与分解,目的在于把一些复杂的运动简化为比较简单的直线运动。
运动合成与分解的内容:位移、速度、加速度。
运动合成与分解的方法——平行四边形定则。
运动的合成与分解的解题要点:
1.在实际解题时,经常用到平行四边形定则,应注意掌握
2.认真分析谁是合运动、谁是分运动。
(一般说来,能够观察到(真实)的运动是合运动)
3.要注意寻求分运动效果。
4.合运动与分运动具有:等时性、独立性、等效性。
5.分析此类问题的一般方法:运动合成分解法、微元法。
第一章
抛体运动复习
【方法提示】
根据运动效果认真做好运动矢量图,是解题的关键。
【问题综述】
V1为水流速度,V2为船相对于静水的速度,θ为V1与V2的夹角,L为河宽。
沿水流方向:速度为V∥=V1+V2cosθ的匀速直线运动
垂直河岸方向:速度为V⊥=V2sinθ的匀速直线运动(渡河)
①欲使船垂直渡河,V∥=0
②欲使船垂直渡河时间最短,θ=900
第一章
抛体运动复习
【答案】①θ=600
②垂直于河岸
运动矢量分析
【例题】一船准备渡河,已知水流速度为V0=1m/s,船在
静水中的航速为V’=2m/s,则:
①要使船能够垂直地渡过河去,那么应向何方划船?
②要使船能在最短时间内渡河,应向何方划船?
第一章
抛体运动复习
运动矢量分析
【答案】
Vmin=2.4m/s
【例题】一人横渡40米宽的河,河水流速3
m/s,下游距下水30米处有一拦河坝,为保证安全渡河,此人相对于水的速度至少为多少?
第一章
抛体运动复习
运动矢量分析
【答案】θ=600
Vmin≈173m
【例题】小孩游泳的速度是河水流速的二分之一,河宽d=100m,问小孩向什么方向游向对岸,才能使他被河水冲行的距离最短?这最短的距离是多少?
第一章
抛体运动复习
【问题综述】
此类问题的关键是:
1.准确判断谁是合运动,谁是分运动;实际运动是合运动
2.根据运动效果寻找分运动;
3.一般情况下,分运动表现在:
①沿绳方向的伸长或收缩运动;
②垂直于绳方向的旋转运动。
4.根据运动效果认真做好运动矢量图,是解题的关键
5.对多个用绳连接的物体系统,要牢记在绳的方向上
的速度大小相等。
6.此类问题还经常用到微元法求解。
第一章
抛体运动复习
【答案】
寻找分运动效果
减速
【例题】如图所示,纤绳以恒定速率V
沿水平方向通过定滑轮牵引小船靠岸,当纤绳与水面夹角为θ时,船靠岸的速度是
,若使船匀速靠岸,则纤绳的速度是
。(填:匀速、加速、减速)
第一章
抛体运动复习
【例题】如图所示,汽车沿水平路面以恒定速度v前进,则当拉绳与水平方向成θ角时,被吊起的物体M
的速度为vM=
。
【答案】
寻找分运动效果
VM=V·cosθ
第一章
抛体运动复习
竖直上抛运动的处理方法
由于竖直上抛运动涉及上升和下降两个过程,因此在处理竖直上抛运动问题时,常有以下两种思路:
⑴分步处理
①上升过程当作匀减速直线运动
②下降过程当作匀加速直线运动(自由落体运动)
⑵整体处理
就整体而言,竖直上抛运动是一种匀变速直线运动,加速度为g,解题中注意各物理量的符号。
在实际问题中。选取哪种方法进行处理,应视问题的方便而定。
第一章
抛体运动复习
竖直上抛运动的规律:
解题时,认真作出矢量图,注意物理量的方向。
1.平抛运动(常规)分解为:
①水平方向的匀速直线运动;
②竖直方向的自由落体运动。
2.斜抛运动(常规)分解为:
①水平方向的匀速直线运动;
②竖直方向的竖直上抛运动。
第一章
抛体运动复习
第一章
抛体运动复习
做平抛运动的物体落在斜面上
物体从斜面上平抛又落回到斜面
可得知两分速度与斜面间的夹角。
可得知两分位移间的几何关系。
当合速度平行于斜面时,物体离斜面最远。
以v0的水平初速度抛出一物体,飞行一段时间后,垂直地撞在倾角为a的斜面上,则物体飞行的时间是多少?
第一章
抛体运动复习
实验的注意事项
每次小球均从同一高度下落
斜槽末端水平
数据处理
根据各点间的水平距离判定时间间隔
根据相同时间间隔内竖直位移关系判断图中第一点是否是平抛运动的起点
第一章
抛体运动复习
研究运动的合成与分解:目的在于把一些复杂的运动简化为比较简单的直线运动。
运动合成与分解的内容:位移、速度、加速度。
运动合成与分解的方法——平行四边形定则。
绳子拉物体一般情况下,分运动表现在:
①沿绳方向的伸长或收缩运动;
②垂直于绳方向的旋转运动
第一章
抛体运动复习
研究抛体运动时:通常是将一个复杂的运动分解成两个相互垂直直线运动。如:平抛运动——分解为水平方向的匀速直线运动和竖直方向的自由落体运动;又如:斜抛运动——分解为水平方向的匀速直线运动的竖直方向的竖直上抛运动。
o
x
y
A
平抛运动
水平坐标:x=v0t
竖直坐标:y=gt2/2
速度公式:
Vx=Vo
Vy=gt
第一章
抛体运动复习
运动中的“微元法”实质是:
在运动的过程中,选取一微小时间△t,在此时间内,运动物体发生一微小位移,然后利用数学极限思想,对运动进行分析。
由于运动时间极短,所以不论物体做何种运动,都可看成做匀速直线运动。
这种方法由于涉及高深数学理论,所以在高中并不常用。但它却是解决连续变化物理量的求解的最基础、最适用的方法。
第一章
抛体运动复习
例1:船在静水中的速度v1=4m/s,河水速度v2=3m/s,河宽200m
求(1)船以最短时间过河,船头向何方开去,所用时间多少?
(2)船以最短位移过河,船头向何方开去,所用时间多少,速度多大?
解:(1)船头总是垂直河岸过河,所以时间最短:t=s/v1=50s
(2)船以最短位移过河,合位移垂直河岸v=√7
m/s
船头与河岸成α角向上游开去tanα
=√7
/3
时间:t=s/v=200/√7
例2
一艘小船在
200m宽的河中横渡到对岸,已知水流速度是2m/s,小船在静水中的速度是4m/s,求:
①当船头始终正对着对岸时,小船多长时间到达对岸,小船实际运行了多远?
②如果小船的路径要与河岸垂直,应如何行驶?消耗的时间是多少?
③如果小船要用最短时间过河,应如何?船行最短时间为多少??
简答:
①在解答本题的时候可由此提问:船头始终正对河岸代表什么含义.(①题的答案:50秒,下游100米)
②路径与河岸垂直——船的实际运动——船的合运动(在两个分运动的中间,并与河岸垂直)(②题的答案:与上游河岸成60°,57.7s)
③分析本题,可以得到求t最小的方法:
1、河宽一定,要想使时间最少应使垂直河岸方向的分速度最大,即正对河岸航行,则
2、或者由
三个式子一一分析
一定,
又有最小值,即河宽,便可以求出渡河最短时间.
(③题的答案:50s)
例3
在高处拉低处小船时,通常在河岸上通过滑轮用钢绳拴船,若拉绳的速度为4m/s,当拴船的绳与水平方向成60°时,船的速度是多少?(8m/s)
?????????????????????????????????????????????????????????????????????????????????????????????????????
上题提示:(提示:在分析船的运动时,我们发现船的运动产生了两个运动效果:绳子在不断缩短;而且绳子与河岸的夹角不断减小,所以我们可以将船的运动——实际运动——合运动分解成沿绳子方向的运动和垂直绳子方向所做的圆周运动)
1、船沿水平方向前进——此方向为合运动,求合速度v.
2、小船的运动可以看成为沿绳子缩短方向的运动和垂直绳子方向做圆周运动的合运动.
1、关于运动的合成与分解的说法中,正确的是(??
)
A、合运动的位移为分运动的位移的矢量和.
B、合运动的速度一定比其中一个分速度大.
C、合运动的时间为分运动时间之和.
D、合运动的时间与各分运动时间相等
AD
