人教版高二物理必修二曲线运动复习课(共28张PPT)
文档属性
| 名称 | 人教版高二物理必修二曲线运动复习课(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 987.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-06-03 08:08:29 | ||
图片预览







文档简介
(共35张PPT)
曲线运动复习课
曲线运动
曲线运动的条件
曲线运动的研究方法
运动的合成
运动的分解
主要是正交分解
典型的曲线运动模型
平抛运动
圆周运动
水平匀速圆周运动
竖直平面圆周运动
重点,难点
离心现象
只要求掌握最高点和最低点的分析
会分析实例
描述它的物理量v,ω,T,an,及它所遵循的动力学规律
Fn=man
重点,难点
一 曲线运动的特点及条件
从运动学角度看:
1.运动方向时刻改变,是变速运动。
2.质点的速度方向沿轨道的切线方向。
3.变速运动一定有加速度。
从动力学角度看:(曲线运动的条件)
合外力方向(或加速度方向)跟速度方
向不在同一条直线上。
三种典型的曲线运动:
1.平抛运动
2.圆周运动
3.离心现象
例1.下列关于曲线运动的描述中,正确的是(
)
A.曲线运动可以是匀速运动
B.曲线运动一定是变速运动
C.曲线运动可以是匀变速运动
D.曲线运动的加速度可能为零
BC
如何把复杂的曲线运动转变成简单的运动?
平行四边形法则
二 运动的合成与分解
运动的合成与分解要注意______和_______
等时性
独立性
等时性:合运动所需时间和对应的每个分运动所需时
间相等.
独立性:一个物体可以同时参与几个不同的分运动,
各个分运动独立进行,互不影响.
2、以下关于分运动和合运动的关系的讨论中,正确的说法是:(
)
A.两个直线运动的合运动,可能是直线运动,也可能是曲线运动;
B.两个匀速直线运动的合运动,可能是直线运动,也可能是曲线运动;
C.两个匀变速直线运动的合运动,可能是直线运动,也可能是曲线运动;
D.两个分运动的运动时间,一定与它们的合运动的运动时间相等。
ACD
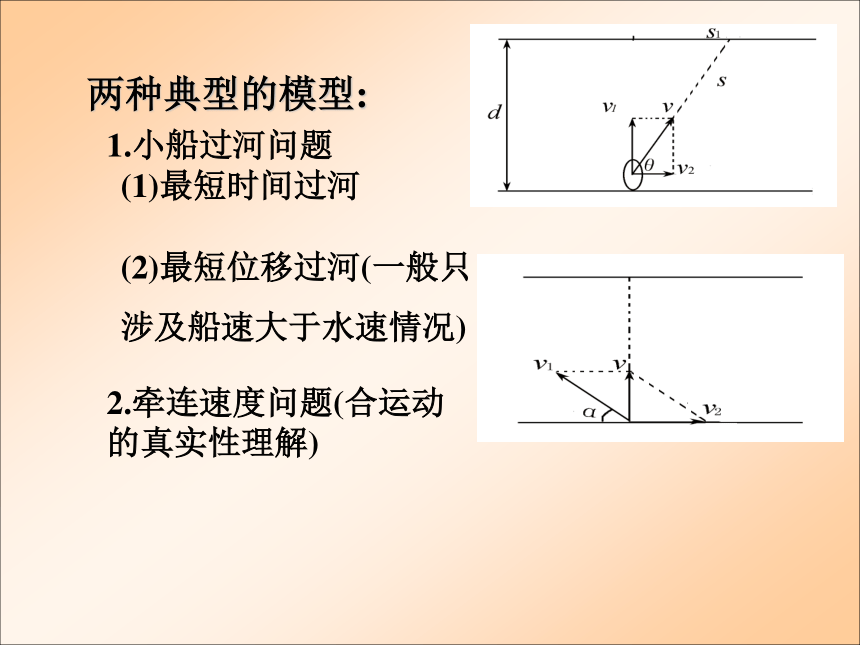
两种典型的模型:
1.小船过河问题
(1)最短时间过河
(2)最短位移过河(一般只
涉及船速大于水速情况)
2.牵连速度问题(合运动的真实性理解)
小船在静水中速度为3m/s。它在一条流速为4m/s,河宽为150m的河流中横渡,则(
)
A.小船不可能垂直河岸正达对岸
B.小船渡河时间可能为40s
C.小船渡河时间至少需30s
D.小船若在50s内渡河,到对岸时被冲下150m
小船过河
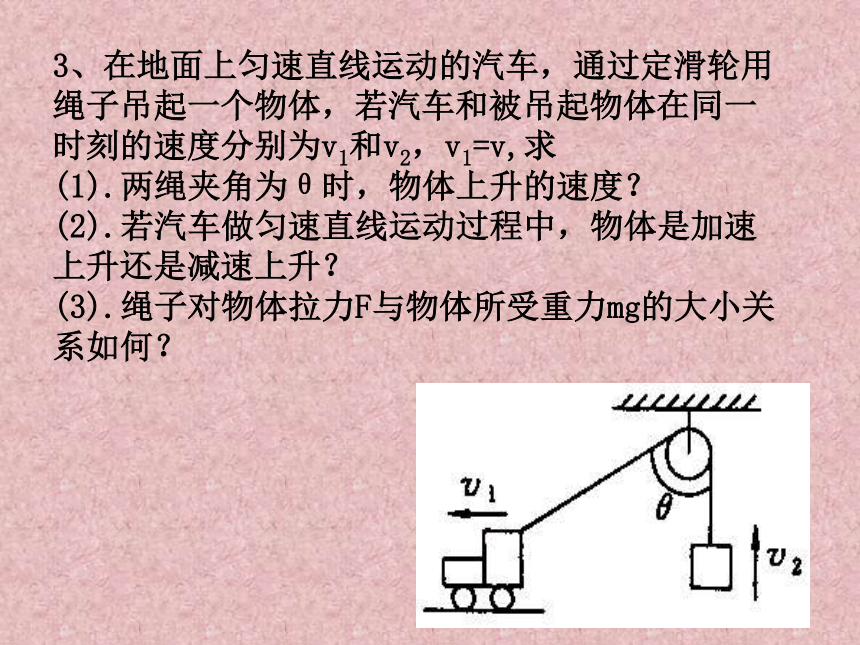
3、在地面上匀速直线运动的汽车,通过定滑轮用绳子吊起一个物体,若汽车和被吊起物体在同一时刻的速度分别为v1和v2,v1=v,求
(1).两绳夹角为θ时,物体上升的速度?
(2).若汽车做匀速直线运动过程中,物体是加速上升还是减速上升?
(3).绳子对物体拉力F与物体所受重力mg的大小关系如何?
①特征:只受重力,初速度沿水平方向。
②规律:水平方向上的匀速直线运动和竖直方向上的自由落体运动的合运动(匀变速曲线运动a=g)
水平分运动:
水平位移:
x=
vo
t
水平分速度:vx
=
vo
竖直分运动:
竖直位移:
y
=
g
t2
竖直分速度:vy=
g
t
合位移
S=
tanα=
合速度
V
=
tan?
=
三 平抛运动规律及应用
例4:月球上的“重力加速度”大约是地球上重力加速度的1/6.如果分别在月球和地球上做平抛运动,且其高度h和水平初速度V0都相等,则其水平距离之比为:______.
√6
:
1
例5:在水平地面上,有一小球A从某点以初速度vA0=8m/s向右匀加速直线运动。同时,在A球的正上方高h=20m处,另一小球B以水平速度vB=10m/s向右抛出,球B落地时刚好砸在小球A上。不计空气阻力,g取10m/s2,求:
(1)两小球相碰时,A球速度的大小?(2)球A的加速度?
vA
=12m/s
a=2m/s2
1
特征:轨迹为圆,速率不变,方向时刻改变的变速运动。
2
线速度:大小:V=
=
单位:m/s;
方向:圆上各点的切线方向。
3
角速度:大小:?=
单位:rad/s;
4
周期与频率的关系:T=1/f=1/n(n为转速
单位:/s)
5
线速度与角速度的关系:v=?R
同轴转动,齿轮传动,皮带轮传动时角速度与线速度的关系。
四 匀速圆周运动
例6:如图所示装置中,三个轮的半径分别为r、2r、4r,b点到圆心的距离为r,求图中a、b、c、d各点的线速度之比、角速度之比。
线速度之比:
2
:
1
:
2
:
4
角速度之比:
2
:
1
:
1
:
1
6
向心加速度,向心力
向心加速度:
①大小:a
=
②方向:时刻指向圆心。
向心力:
①作用:使物体做圆周运动,只改变速度方向,不改变速度大小。
②来源:一个力或几个力的合力、或某一个力的分力,是效果力。
③方向:F向⊥v,指向圆心。
④大小:
例7:一根长为0.5m的细绳,当它受到5N的拉力会被拉断,现在它的一端拴着一个质量为0.4㎏的小球,以另一端为中心,使小球在光滑的水平面上做匀速圆周运动,问:
(1).绳子被拉断时,小球的角速度至少为多大?拉断绳子后的小球将做什么运动?
(2).若使物体在竖直平面内做圆周运动,当它经过最低点时能将绳子拉断的线速度至少是多少?拉断绳子后的小球将做什么运动?
?=5
rad/s;
匀速直线运动
v=1.5
m/s;
平抛运动
总结:匀速圆周运动解题步骤
1明确研究对象
2受力分析
3确定”圆轨道平面和圆心”
4明确”向心力来源”
5根据牛顿运动定律列方程求解
常见的水平面内匀速圆周运动:
五 竖直平面内的圆周运动:
竖直平面内的圆周运动是典型的变速圆周运动,时常与能量及动量相结合,中学物理中只研究物体在最高点与最低点的两种情况.主要有以下两种类型:
1.如图4-4-1所示:无支撑物的小球在竖直平面内最高点情况.
图4-4-1
(1)临界条件:小球达最高点时绳子的拉力(或轨道的弹力)刚好等于0,小球在最高点的向心力全部由重力来提供,这时有mg=mv2min/r,式中的vmin是小球通过最高点的最小速度,通常叫临界速度vmin=
.
(2)能通过最高点的条件:v≥vmin.
(3)不能通过最高点条件v<vmin。注意的是这是假设到最高点而做出一个v,其实球没到最高点就脱离了轨道或是沿原轨道返回或是做斜抛运动了.
2.如图4-4-2所示:有支撑物的小球在竖直平面内最高点情况.
图4-4-2
(1)临界条件:由于硬杆和管壁的支撑作用,小球恰好能到最高点的临界速度vmin=0.
(2)当v=0时,轻杆对小球有竖直向上的支持力N,其大小等于小球的重力,即N=mg;
当0<v<
时,杆对小球的支持力的方向竖直向上,大小随速度增大而减小,其取值范围是:0<N<mg;
当v=
时,N=0;
当v>
时,杆对小球有指向圆心的拉力,其大小随速度的增大而增大.
以上两种类型在最低点的情况相同:
常见的竖直平面内的圆周运动:
F拉-mg=mv2/r 或
FN-mg=mv2/r
[练习题1]质量相等的小球A、B分别固定在轻杆的中点及端点,
当棒在光滑的水平面上绕O点匀速运动(如图所示)时,求棒的OA段及AB段对球的拉力之比。
T1
T2
T2
T1-T2=m
ω2rOA
①
T2=m
ω2rOB
②
rOA
=rOB/2
③
T1/T2=3/2
[练习题2]如图,质量为M的物体内有光滑圆形轨道,现有一质量为m的小滑块沿该圆形轨道在竖直面内作圆周运动。A、C点为圆周的最高点和最低点,B、D点是与圆心O同一水平线上的点。小滑块运动时,物体M在地面上静止不动,则物体M对地面的压力F和地面对M的摩擦力有关说法正确的是
(
)
A.小滑块在A点时,F>Mg,M与地面无摩擦
B.小滑块在B点时,F=Mg,摩擦力方向向右
C.小滑块在C点时,F=(M+m)g,M与地面无摩擦
D.小滑块在D点时,F=(M+m)g,摩擦力方向向左
B
[练习题2]一小球用长为L的细绳悬挂于O点,为使小球能绕O点在竖直面内做圆周运动,则小球的最低点处至少需要获得多大的水平速度v0
?
O
L
v
v0
T
mg
mg
解:设小球在最高点所须的最小速度(临界值)为v,则
g=mv2/L
①
又机械能守恒,故有
2mgL=mv02/2-
mv2/2
③
由①
②
③三式可得
习题1:如图所示,两个小球A和B分别被两条轻绳系住,在同一平面内做圆锥摆运动,已知系B的绳子与竖直线的夹角为θ,而系A的绳子与竖直线的夹角为2θ,关于A、B两小球运动的周期之比,下列说法中正确的是(
)
A.1:2
B.2:1
C.1:4
D.1:1
D
曲线运动复习课
曲线运动
曲线运动的条件
曲线运动的研究方法
运动的合成
运动的分解
主要是正交分解
典型的曲线运动模型
平抛运动
圆周运动
水平匀速圆周运动
竖直平面圆周运动
重点,难点
离心现象
只要求掌握最高点和最低点的分析
会分析实例
描述它的物理量v,ω,T,an,及它所遵循的动力学规律
Fn=man
重点,难点
一 曲线运动的特点及条件
从运动学角度看:
1.运动方向时刻改变,是变速运动。
2.质点的速度方向沿轨道的切线方向。
3.变速运动一定有加速度。
从动力学角度看:(曲线运动的条件)
合外力方向(或加速度方向)跟速度方
向不在同一条直线上。
三种典型的曲线运动:
1.平抛运动
2.圆周运动
3.离心现象
例1.下列关于曲线运动的描述中,正确的是(
)
A.曲线运动可以是匀速运动
B.曲线运动一定是变速运动
C.曲线运动可以是匀变速运动
D.曲线运动的加速度可能为零
BC
如何把复杂的曲线运动转变成简单的运动?
平行四边形法则
二 运动的合成与分解
运动的合成与分解要注意______和_______
等时性
独立性
等时性:合运动所需时间和对应的每个分运动所需时
间相等.
独立性:一个物体可以同时参与几个不同的分运动,
各个分运动独立进行,互不影响.
2、以下关于分运动和合运动的关系的讨论中,正确的说法是:(
)
A.两个直线运动的合运动,可能是直线运动,也可能是曲线运动;
B.两个匀速直线运动的合运动,可能是直线运动,也可能是曲线运动;
C.两个匀变速直线运动的合运动,可能是直线运动,也可能是曲线运动;
D.两个分运动的运动时间,一定与它们的合运动的运动时间相等。
ACD
两种典型的模型:
1.小船过河问题
(1)最短时间过河
(2)最短位移过河(一般只
涉及船速大于水速情况)
2.牵连速度问题(合运动的真实性理解)
小船在静水中速度为3m/s。它在一条流速为4m/s,河宽为150m的河流中横渡,则(
)
A.小船不可能垂直河岸正达对岸
B.小船渡河时间可能为40s
C.小船渡河时间至少需30s
D.小船若在50s内渡河,到对岸时被冲下150m
小船过河
3、在地面上匀速直线运动的汽车,通过定滑轮用绳子吊起一个物体,若汽车和被吊起物体在同一时刻的速度分别为v1和v2,v1=v,求
(1).两绳夹角为θ时,物体上升的速度?
(2).若汽车做匀速直线运动过程中,物体是加速上升还是减速上升?
(3).绳子对物体拉力F与物体所受重力mg的大小关系如何?
①特征:只受重力,初速度沿水平方向。
②规律:水平方向上的匀速直线运动和竖直方向上的自由落体运动的合运动(匀变速曲线运动a=g)
水平分运动:
水平位移:
x=
vo
t
水平分速度:vx
=
vo
竖直分运动:
竖直位移:
y
=
g
t2
竖直分速度:vy=
g
t
合位移
S=
tanα=
合速度
V
=
tan?
=
三 平抛运动规律及应用
例4:月球上的“重力加速度”大约是地球上重力加速度的1/6.如果分别在月球和地球上做平抛运动,且其高度h和水平初速度V0都相等,则其水平距离之比为:______.
√6
:
1
例5:在水平地面上,有一小球A从某点以初速度vA0=8m/s向右匀加速直线运动。同时,在A球的正上方高h=20m处,另一小球B以水平速度vB=10m/s向右抛出,球B落地时刚好砸在小球A上。不计空气阻力,g取10m/s2,求:
(1)两小球相碰时,A球速度的大小?(2)球A的加速度?
vA
=12m/s
a=2m/s2
1
特征:轨迹为圆,速率不变,方向时刻改变的变速运动。
2
线速度:大小:V=
=
单位:m/s;
方向:圆上各点的切线方向。
3
角速度:大小:?=
单位:rad/s;
4
周期与频率的关系:T=1/f=1/n(n为转速
单位:/s)
5
线速度与角速度的关系:v=?R
同轴转动,齿轮传动,皮带轮传动时角速度与线速度的关系。
四 匀速圆周运动
例6:如图所示装置中,三个轮的半径分别为r、2r、4r,b点到圆心的距离为r,求图中a、b、c、d各点的线速度之比、角速度之比。
线速度之比:
2
:
1
:
2
:
4
角速度之比:
2
:
1
:
1
:
1
6
向心加速度,向心力
向心加速度:
①大小:a
=
②方向:时刻指向圆心。
向心力:
①作用:使物体做圆周运动,只改变速度方向,不改变速度大小。
②来源:一个力或几个力的合力、或某一个力的分力,是效果力。
③方向:F向⊥v,指向圆心。
④大小:
例7:一根长为0.5m的细绳,当它受到5N的拉力会被拉断,现在它的一端拴着一个质量为0.4㎏的小球,以另一端为中心,使小球在光滑的水平面上做匀速圆周运动,问:
(1).绳子被拉断时,小球的角速度至少为多大?拉断绳子后的小球将做什么运动?
(2).若使物体在竖直平面内做圆周运动,当它经过最低点时能将绳子拉断的线速度至少是多少?拉断绳子后的小球将做什么运动?
?=5
rad/s;
匀速直线运动
v=1.5
m/s;
平抛运动
总结:匀速圆周运动解题步骤
1明确研究对象
2受力分析
3确定”圆轨道平面和圆心”
4明确”向心力来源”
5根据牛顿运动定律列方程求解
常见的水平面内匀速圆周运动:
五 竖直平面内的圆周运动:
竖直平面内的圆周运动是典型的变速圆周运动,时常与能量及动量相结合,中学物理中只研究物体在最高点与最低点的两种情况.主要有以下两种类型:
1.如图4-4-1所示:无支撑物的小球在竖直平面内最高点情况.
图4-4-1
(1)临界条件:小球达最高点时绳子的拉力(或轨道的弹力)刚好等于0,小球在最高点的向心力全部由重力来提供,这时有mg=mv2min/r,式中的vmin是小球通过最高点的最小速度,通常叫临界速度vmin=
.
(2)能通过最高点的条件:v≥vmin.
(3)不能通过最高点条件v<vmin。注意的是这是假设到最高点而做出一个v,其实球没到最高点就脱离了轨道或是沿原轨道返回或是做斜抛运动了.
2.如图4-4-2所示:有支撑物的小球在竖直平面内最高点情况.
图4-4-2
(1)临界条件:由于硬杆和管壁的支撑作用,小球恰好能到最高点的临界速度vmin=0.
(2)当v=0时,轻杆对小球有竖直向上的支持力N,其大小等于小球的重力,即N=mg;
当0<v<
时,杆对小球的支持力的方向竖直向上,大小随速度增大而减小,其取值范围是:0<N<mg;
当v=
时,N=0;
当v>
时,杆对小球有指向圆心的拉力,其大小随速度的增大而增大.
以上两种类型在最低点的情况相同:
常见的竖直平面内的圆周运动:
F拉-mg=mv2/r 或
FN-mg=mv2/r
[练习题1]质量相等的小球A、B分别固定在轻杆的中点及端点,
当棒在光滑的水平面上绕O点匀速运动(如图所示)时,求棒的OA段及AB段对球的拉力之比。
T1
T2
T2
T1-T2=m
ω2rOA
①
T2=m
ω2rOB
②
rOA
=rOB/2
③
T1/T2=3/2
[练习题2]如图,质量为M的物体内有光滑圆形轨道,现有一质量为m的小滑块沿该圆形轨道在竖直面内作圆周运动。A、C点为圆周的最高点和最低点,B、D点是与圆心O同一水平线上的点。小滑块运动时,物体M在地面上静止不动,则物体M对地面的压力F和地面对M的摩擦力有关说法正确的是
(
)
A.小滑块在A点时,F>Mg,M与地面无摩擦
B.小滑块在B点时,F=Mg,摩擦力方向向右
C.小滑块在C点时,F=(M+m)g,M与地面无摩擦
D.小滑块在D点时,F=(M+m)g,摩擦力方向向左
B
[练习题2]一小球用长为L的细绳悬挂于O点,为使小球能绕O点在竖直面内做圆周运动,则小球的最低点处至少需要获得多大的水平速度v0
?
O
L
v
v0
T
mg
mg
解:设小球在最高点所须的最小速度(临界值)为v,则
g=mv2/L
①
又机械能守恒,故有
2mgL=mv02/2-
mv2/2
③
由①
②
③三式可得
习题1:如图所示,两个小球A和B分别被两条轻绳系住,在同一平面内做圆锥摆运动,已知系B的绳子与竖直线的夹角为θ,而系A的绳子与竖直线的夹角为2θ,关于A、B两小球运动的周期之比,下列说法中正确的是(
)
A.1:2
B.2:1
C.1:4
D.1:1
D
