人教版数学八年级下册第19.1变量与函数同步测试题(含答案)
文档属性
| 名称 | 人教版数学八年级下册第19.1变量与函数同步测试题(含答案) | 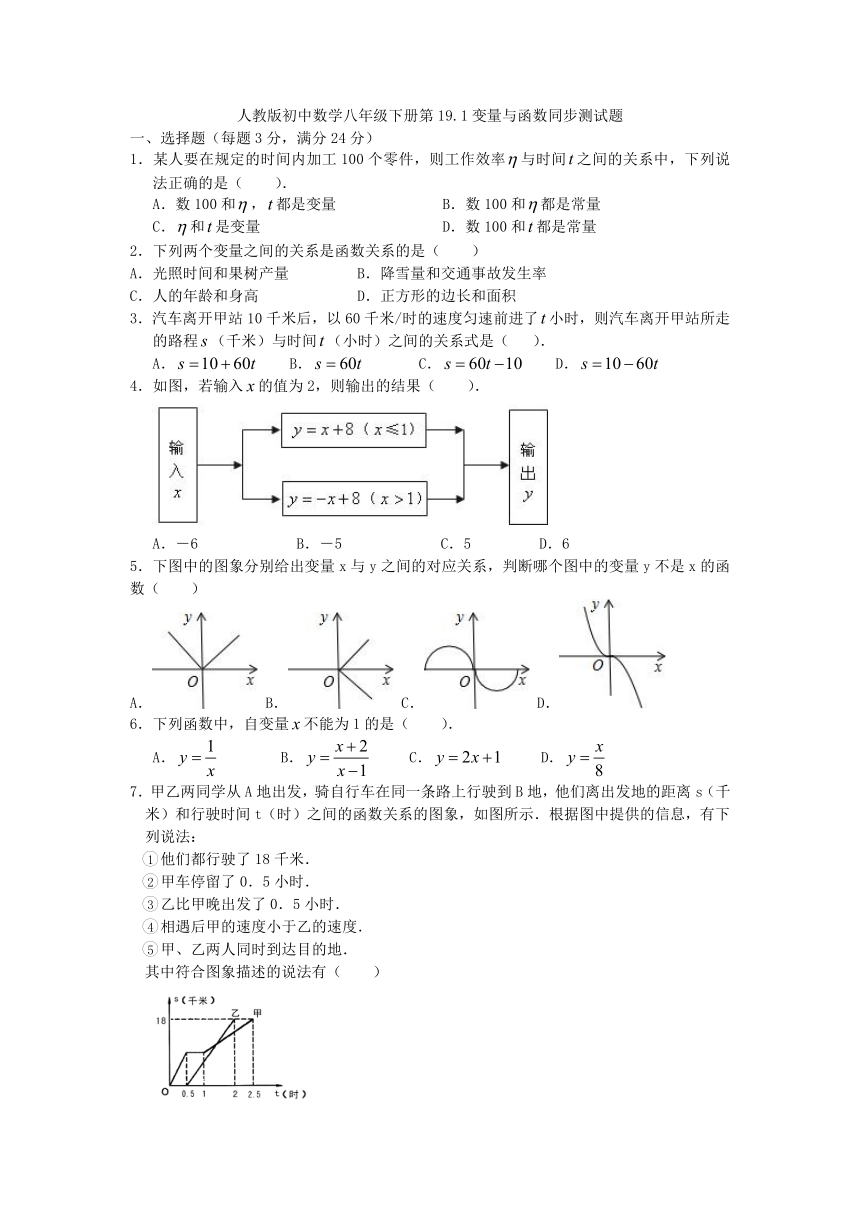 | |
| 格式 | zip | ||
| 文件大小 | 309.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-03 07:02:17 | ||
图片预览



文档简介
人教版初中数学八年级下册第19.1变量与函数同步测试题
一、选择题(每题3分,满分24分)
1.某人要在规定的时间内加工100个零件,则工作效率与时间之间的关系中,下列说法正确的是(
).
A.数100和,都是变量
B.数100和都是常量
C.和是变量
D.数100和都是常量
2.下列两个变量之间的关系是函数关系的是( )
A.光照时间和果树产量
B.降雪量和交通事故发生率
C.人的年龄和身高
D.正方形的边长和面积
3.汽车离开甲站10千米后,以60千米/时的速度匀速前进了小时,则汽车离开甲站所走的路程(千米)与时间(小时)之间的关系式是(
).
A.
B.
C.
D.
4.如图,若输入的值为2,则输出的结果(
).
A.―6
B.―5
C.5
D.6
5.下图中的图象分别给出变量x与y之间的对应关系,判断哪个图中的变量y不是x的函数( )
A.
B.
C.
D.
6.下列函数中,自变量不能为1的是(
).
A.
B.
C.
D.
7.甲乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(时)之间的函数关系的图象,如图所示.根据图中提供的信息,有下列说法:
1
他们都行驶了18千米.
2
甲车停留了0.5小时.
3
乙比甲晚出发了0.5小时.
4
相遇后甲的速度小于乙的速度.
5
甲、乙两人同时到达目的地.
其中符合图象描述的说法有(
)
A.2个
B.3个
C.4个
D.5个
8.如图,四幅图象分别表示变量之间的关系,请按图象的顺序,将下面的四种情境与之对应排序.
①
②
③
④
运动员推出去的铅球(铅球的高度与时间的关系)
静止的小车从光滑的斜面滑下(小车的速度与时间的关系)
一个弹簧由不挂重物到所挂重物的质量逐渐增加(弹簧的长度与所挂重物的质量的关系)
小明从A地到B地后,停留一段时间,然后按原速度原路返回(小明离A地的距离与时间的关系)
正确的顺序是(
)
A.
B.
C.
D.
二、填空题(每题4分,满分32分)
9.在圆的面积公式S=πR2中,π是_________(填“常量”或“变量”),S和R是_________(填“常量”或“变量”).
10.函数是表达现实世界中数量之间变化规律的一种数学模型,它的三种数学表示方法分别为_________、_________、_________.
11.如图,表示一辆汽车行驶的速度和时间的图象,你能用语言描述汽车的行驶情况吗?________________________________.
12.函数中自变量的取值范围是______________.
13.已知等式,则关于的函数关系式为________________.
14.球的飞行高度h(m)与飞行时间t(s)之间的关系式为h=20t-5t2,则t=
1或3秒时,球的飞行高度为______________.
15.假定甲、乙两人在一次赛跑中,路程S与时间t的关系如图所示,看图填空:
?
(1)这是一次_______赛跑.(2)甲、乙两人中先到达终点的是_________.
(3)乙在这次赛跑中的平均速度是_________/.
16.如图,表示甲骑电动自行车和乙驾驶汽车的均行驶90km的过程中,行驶的路程与经过的时间之间的函数关系,请根据图象填空:
_________出发的早,早了________小时,_____________先到达,先到_________小时,电动自行车的速度为__________km/h,汽车的速度为__________km/h.
三、解答题(满分44分)
17.已知长方形的相邻两边的长分别是xcm和4cm,设长方形的周长为ycm.
①试写出长方形的周长y与x之间的关系式;
②求当x长为10cm,15cm时的周长;
③求当周长分别为20cm,30cm时的x值.
18.某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同.他们将一头骆驼前两昼夜的体温变化情况绘制成下图(如图8).请根据图象回答:
⑴第一天中,在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要
多少时间?
⑵第三天12时这头骆驼的体温是多少?
19.下表是佳佳往小姨家打长途电话的几次收费标准记录:
时间x(分)
1
2
3
4
5
6
7
电话费y(元)
0.6
1.2
1.8
2.4
3.0
3.6
4.2
回答下列问题:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)帮助佳佳预测一下,如果她打电话用的时间是10分钟,那么需要付多少电话费;
(3)请你写出通话时间x(分钟)(x为正整数)与所要付的电话费y(元)之间的关系式.
20.(1)小亮参加智力竞赛,基础分为100分,然后每答对一个问题得10分.
①写出他答对了x个问题与总得分y之间的函数关系式;
②指出函数关系式中的常量、变量、函数;
③当他答对了10个问题时,求函数的值.
(2)小明准备到新华书店为班级购买44本课外读物,如果每本定价为9.80元,他带了450元人民币,请你估计他带的钱够不够用?并说明理由.
21.(10分)某校组织学生到距学校6千米的光明科技馆参观,学生王红因事没能乘上学校的包车,于是准备在学校门口改乘出租车去明科技馆,出租车收费标准如下:
里程(千米)
收费(元)
3千米以下(含3千米)
8.00
3千米以上,每增加1千米
1.80
(1)写出出租车行驶的里程数x与费用y之间的函数关系式;
(2)王红同学身上仅有14元钱,乘出租车到科技馆的车费够不够?请说明理由.
22.下表是天马冰箱厂2019年前半年每个月的产量:
x(月)
1
2
3
4
5
6
y(台)
10000
10000
12000
13000
14000
18000
(1)根据表格中的数据,你能否根据x的变化,得到y的变化趋势?
(2)根据表格你知道哪几个月的月产量保持不变?哪几个月月产量在匀速增长?哪几个月产量最高?
(3)试求2019年前半年的平均月产量是多少?
分析:用表格表示现实生活中的数量关系,简明易懂,便于寻找变化规律,估计预测未知量,因此在解题时,要仔细观察表格中有关数据是解决本题的关键.
23.小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示).
(1)图象表示了哪两个变量的关系?
(2)10时,他离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)他可能在哪段时间内休息,并吃午餐?
(5)他由离家最远的地方返回时的平均速度是多少?
24.填表并观察下列两个函数的变化情况.
x?
?1
2?
3?
?4
?5
…
?y1=10+2x
?
?
?
?
?
?
?y2=5x
?
?
?
?
?
?
(1)在同一个直角坐标系中画出这两个函数的图象,比较它们有什么不同;
(2)预测哪一个函数值先到100.
答案
1.
C
2.
D
3.
A
4.
D
5.
B
6.
B
7.
C
8.
D
9.
常量;
变量
10.
列表法、图象法、
解析式法
11.
汽车以60千米/小时
速度做匀速运动
12.
x≥2
13.
y=4-2x
14.
15m
15.
100比赛;甲;8
16.
甲;2;乙;2;180
17.
解:①根据长方形的周长公式得2(x+4)=y,
∴y=2x+8;
②当x=10cm时,y=2×10+8=28cm,
当x=15时,y=2×15+8=38cm;
③当y=20cm时,2x+8=20,
解得x=6cm,
当y=30cm时,2x+8=30,
解得x=11cm.
18.
分析:本题就是用图象法来表示体温随时间的变化而变化的函数关系
答:⑴第一天中,从4时到16时这头骆驼
的体温是上升的它的体温从最低上升到最高
需要12小时.
⑵第三天12时这头骆驼的体温是39℃.
19.
解:(1)时间与电话费,时间是自变量,电话费是因变量;
(2)打10分钟的电话费为:4.2+(10-7)×0.6=6.0元;
(3)y=0.6x(x为正整数).
20.
解:(1)①由:总得分=基础得分+答题得分,可列出函数解析式:y=10x+100;
②由①中解析式可知10,100均为不变的量,故其为常量;
由于答题正确的个数x是不确定的,其值是变化的,故:变量为x;
每答对x道题对应唯一的得分为(10x+100),
故函数为:y=(10x+100).
③将答对的问题个数x=10代入①中所求的解析式可得总得分=200.
(2)取略大的近似值进行估算,44×10=440元,所以他带钱足够.
21.
解:(1)由表格可知:当x≤3时,y
=8,当x>3时,,故y与x之间的函数关系式为:;
(2)把x=6,代入(1)得:<14,所以,王红乘出租车到科技馆的车费够用.
22.
解:(1)随着月份x的增大,月产量y正在逐渐增加;
(2)1月、2月两个月的月产量不变,3月、4月、5月三个月的产量在匀速增多,6月份产量最高;
(3)(10000+10000+12000+14000+18000)÷6≈13000(台).
故2019年前半年的平均月产量约为13000台.
23.
解:(1)图象表示了距离与时间;
(2)10时,他离家15千米;
(3)他到达离家最远的地方是12时,离家30千米;
(4)他可能在12时到13时间休息,吃午餐;
(5)共用了2时,因此平均速度为30÷2=15千米/时.
24.
解:(1)列表可得:
x?
?1
2?
3?
?4
?5
…
?y1=10+2x
?12
?14
?16
?18
?20
…
?y2=5x
?5
?10
?15
20?
?25
…
在同一个直角坐标系中画出这两个函数的图象,
比较分析可得这两个函数交于点(,);且系数越大函数的图象越靠近y轴.
当x<时,y1>y2,
当x>时,y1<y2;
(2)从函数的图象可知函数y2=5x的函数值先到100.
一、选择题(每题3分,满分24分)
1.某人要在规定的时间内加工100个零件,则工作效率与时间之间的关系中,下列说法正确的是(
).
A.数100和,都是变量
B.数100和都是常量
C.和是变量
D.数100和都是常量
2.下列两个变量之间的关系是函数关系的是( )
A.光照时间和果树产量
B.降雪量和交通事故发生率
C.人的年龄和身高
D.正方形的边长和面积
3.汽车离开甲站10千米后,以60千米/时的速度匀速前进了小时,则汽车离开甲站所走的路程(千米)与时间(小时)之间的关系式是(
).
A.
B.
C.
D.
4.如图,若输入的值为2,则输出的结果(
).
A.―6
B.―5
C.5
D.6
5.下图中的图象分别给出变量x与y之间的对应关系,判断哪个图中的变量y不是x的函数( )
A.
B.
C.
D.
6.下列函数中,自变量不能为1的是(
).
A.
B.
C.
D.
7.甲乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(时)之间的函数关系的图象,如图所示.根据图中提供的信息,有下列说法:
1
他们都行驶了18千米.
2
甲车停留了0.5小时.
3
乙比甲晚出发了0.5小时.
4
相遇后甲的速度小于乙的速度.
5
甲、乙两人同时到达目的地.
其中符合图象描述的说法有(
)
A.2个
B.3个
C.4个
D.5个
8.如图,四幅图象分别表示变量之间的关系,请按图象的顺序,将下面的四种情境与之对应排序.
①
②
③
④
运动员推出去的铅球(铅球的高度与时间的关系)
静止的小车从光滑的斜面滑下(小车的速度与时间的关系)
一个弹簧由不挂重物到所挂重物的质量逐渐增加(弹簧的长度与所挂重物的质量的关系)
小明从A地到B地后,停留一段时间,然后按原速度原路返回(小明离A地的距离与时间的关系)
正确的顺序是(
)
A.
B.
C.
D.
二、填空题(每题4分,满分32分)
9.在圆的面积公式S=πR2中,π是_________(填“常量”或“变量”),S和R是_________(填“常量”或“变量”).
10.函数是表达现实世界中数量之间变化规律的一种数学模型,它的三种数学表示方法分别为_________、_________、_________.
11.如图,表示一辆汽车行驶的速度和时间的图象,你能用语言描述汽车的行驶情况吗?________________________________.
12.函数中自变量的取值范围是______________.
13.已知等式,则关于的函数关系式为________________.
14.球的飞行高度h(m)与飞行时间t(s)之间的关系式为h=20t-5t2,则t=
1或3秒时,球的飞行高度为______________.
15.假定甲、乙两人在一次赛跑中,路程S与时间t的关系如图所示,看图填空:
?
(1)这是一次_______赛跑.(2)甲、乙两人中先到达终点的是_________.
(3)乙在这次赛跑中的平均速度是_________/.
16.如图,表示甲骑电动自行车和乙驾驶汽车的均行驶90km的过程中,行驶的路程与经过的时间之间的函数关系,请根据图象填空:
_________出发的早,早了________小时,_____________先到达,先到_________小时,电动自行车的速度为__________km/h,汽车的速度为__________km/h.
三、解答题(满分44分)
17.已知长方形的相邻两边的长分别是xcm和4cm,设长方形的周长为ycm.
①试写出长方形的周长y与x之间的关系式;
②求当x长为10cm,15cm时的周长;
③求当周长分别为20cm,30cm时的x值.
18.某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同.他们将一头骆驼前两昼夜的体温变化情况绘制成下图(如图8).请根据图象回答:
⑴第一天中,在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要
多少时间?
⑵第三天12时这头骆驼的体温是多少?
19.下表是佳佳往小姨家打长途电话的几次收费标准记录:
时间x(分)
1
2
3
4
5
6
7
电话费y(元)
0.6
1.2
1.8
2.4
3.0
3.6
4.2
回答下列问题:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)帮助佳佳预测一下,如果她打电话用的时间是10分钟,那么需要付多少电话费;
(3)请你写出通话时间x(分钟)(x为正整数)与所要付的电话费y(元)之间的关系式.
20.(1)小亮参加智力竞赛,基础分为100分,然后每答对一个问题得10分.
①写出他答对了x个问题与总得分y之间的函数关系式;
②指出函数关系式中的常量、变量、函数;
③当他答对了10个问题时,求函数的值.
(2)小明准备到新华书店为班级购买44本课外读物,如果每本定价为9.80元,他带了450元人民币,请你估计他带的钱够不够用?并说明理由.
21.(10分)某校组织学生到距学校6千米的光明科技馆参观,学生王红因事没能乘上学校的包车,于是准备在学校门口改乘出租车去明科技馆,出租车收费标准如下:
里程(千米)
收费(元)
3千米以下(含3千米)
8.00
3千米以上,每增加1千米
1.80
(1)写出出租车行驶的里程数x与费用y之间的函数关系式;
(2)王红同学身上仅有14元钱,乘出租车到科技馆的车费够不够?请说明理由.
22.下表是天马冰箱厂2019年前半年每个月的产量:
x(月)
1
2
3
4
5
6
y(台)
10000
10000
12000
13000
14000
18000
(1)根据表格中的数据,你能否根据x的变化,得到y的变化趋势?
(2)根据表格你知道哪几个月的月产量保持不变?哪几个月月产量在匀速增长?哪几个月产量最高?
(3)试求2019年前半年的平均月产量是多少?
分析:用表格表示现实生活中的数量关系,简明易懂,便于寻找变化规律,估计预测未知量,因此在解题时,要仔细观察表格中有关数据是解决本题的关键.
23.小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示).
(1)图象表示了哪两个变量的关系?
(2)10时,他离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)他可能在哪段时间内休息,并吃午餐?
(5)他由离家最远的地方返回时的平均速度是多少?
24.填表并观察下列两个函数的变化情况.
x?
?1
2?
3?
?4
?5
…
?y1=10+2x
?
?
?
?
?
?
?y2=5x
?
?
?
?
?
?
(1)在同一个直角坐标系中画出这两个函数的图象,比较它们有什么不同;
(2)预测哪一个函数值先到100.
答案
1.
C
2.
D
3.
A
4.
D
5.
B
6.
B
7.
C
8.
D
9.
常量;
变量
10.
列表法、图象法、
解析式法
11.
汽车以60千米/小时
速度做匀速运动
12.
x≥2
13.
y=4-2x
14.
15m
15.
100比赛;甲;8
16.
甲;2;乙;2;180
17.
解:①根据长方形的周长公式得2(x+4)=y,
∴y=2x+8;
②当x=10cm时,y=2×10+8=28cm,
当x=15时,y=2×15+8=38cm;
③当y=20cm时,2x+8=20,
解得x=6cm,
当y=30cm时,2x+8=30,
解得x=11cm.
18.
分析:本题就是用图象法来表示体温随时间的变化而变化的函数关系
答:⑴第一天中,从4时到16时这头骆驼
的体温是上升的它的体温从最低上升到最高
需要12小时.
⑵第三天12时这头骆驼的体温是39℃.
19.
解:(1)时间与电话费,时间是自变量,电话费是因变量;
(2)打10分钟的电话费为:4.2+(10-7)×0.6=6.0元;
(3)y=0.6x(x为正整数).
20.
解:(1)①由:总得分=基础得分+答题得分,可列出函数解析式:y=10x+100;
②由①中解析式可知10,100均为不变的量,故其为常量;
由于答题正确的个数x是不确定的,其值是变化的,故:变量为x;
每答对x道题对应唯一的得分为(10x+100),
故函数为:y=(10x+100).
③将答对的问题个数x=10代入①中所求的解析式可得总得分=200.
(2)取略大的近似值进行估算,44×10=440元,所以他带钱足够.
21.
解:(1)由表格可知:当x≤3时,y
=8,当x>3时,,故y与x之间的函数关系式为:;
(2)把x=6,代入(1)得:<14,所以,王红乘出租车到科技馆的车费够用.
22.
解:(1)随着月份x的增大,月产量y正在逐渐增加;
(2)1月、2月两个月的月产量不变,3月、4月、5月三个月的产量在匀速增多,6月份产量最高;
(3)(10000+10000+12000+14000+18000)÷6≈13000(台).
故2019年前半年的平均月产量约为13000台.
23.
解:(1)图象表示了距离与时间;
(2)10时,他离家15千米;
(3)他到达离家最远的地方是12时,离家30千米;
(4)他可能在12时到13时间休息,吃午餐;
(5)共用了2时,因此平均速度为30÷2=15千米/时.
24.
解:(1)列表可得:
x?
?1
2?
3?
?4
?5
…
?y1=10+2x
?12
?14
?16
?18
?20
…
?y2=5x
?5
?10
?15
20?
?25
…
在同一个直角坐标系中画出这两个函数的图象,
比较分析可得这两个函数交于点(,);且系数越大函数的图象越靠近y轴.
当x<时,y1>y2,
当x>时,y1<y2;
(2)从函数的图象可知函数y2=5x的函数值先到100.
