北师大版八年级数学下6.3. 三角形的中位线教学课件 (共26张PPT)
文档属性
| 名称 | 北师大版八年级数学下6.3. 三角形的中位线教学课件 (共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 16.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-03 00:00:00 | ||
图片预览




文档简介
(共26张PPT)
三角形的中位线
F
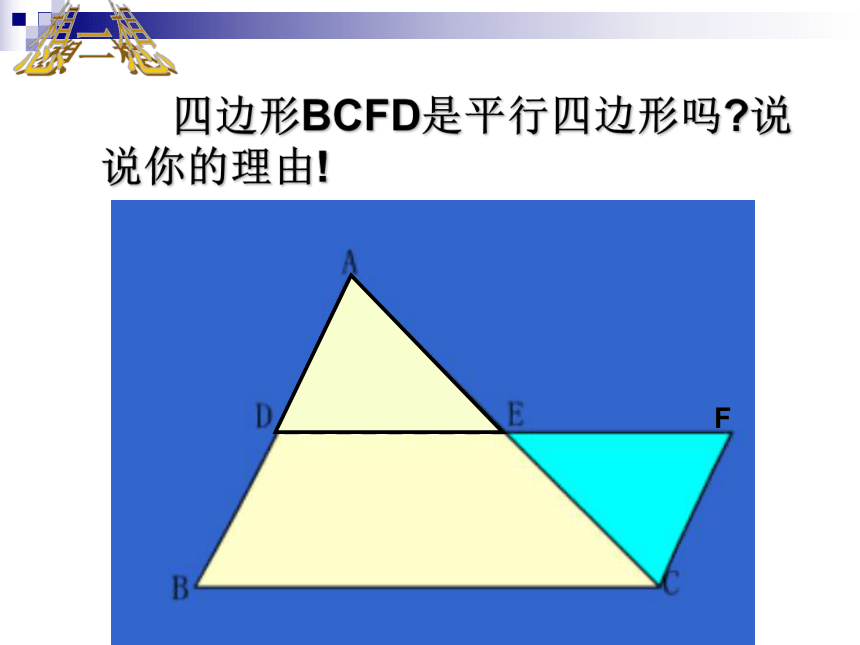
四边形BCFD是平行四边形吗?说说你的理由!
D
E
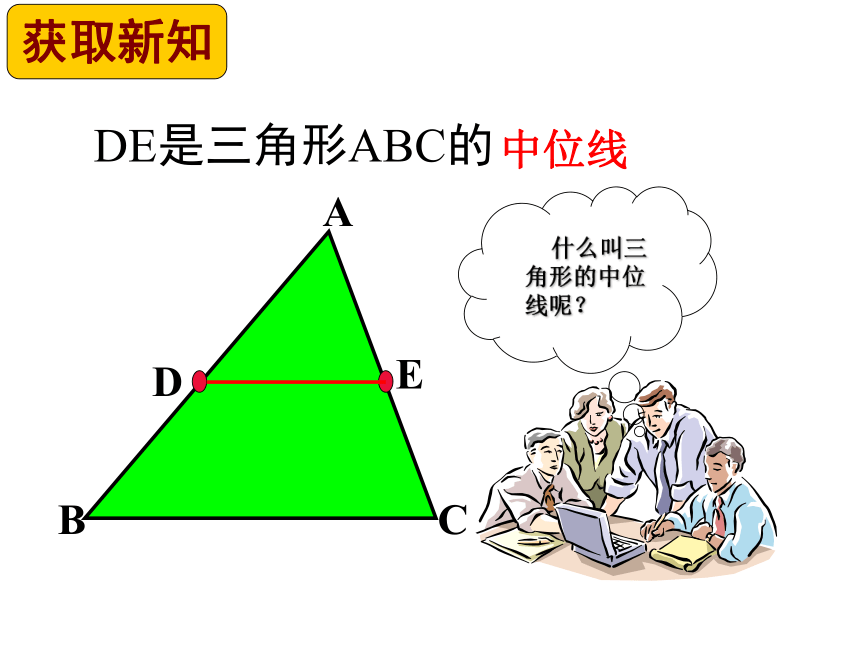
DE是三角形ABC的
中位线
获取新知
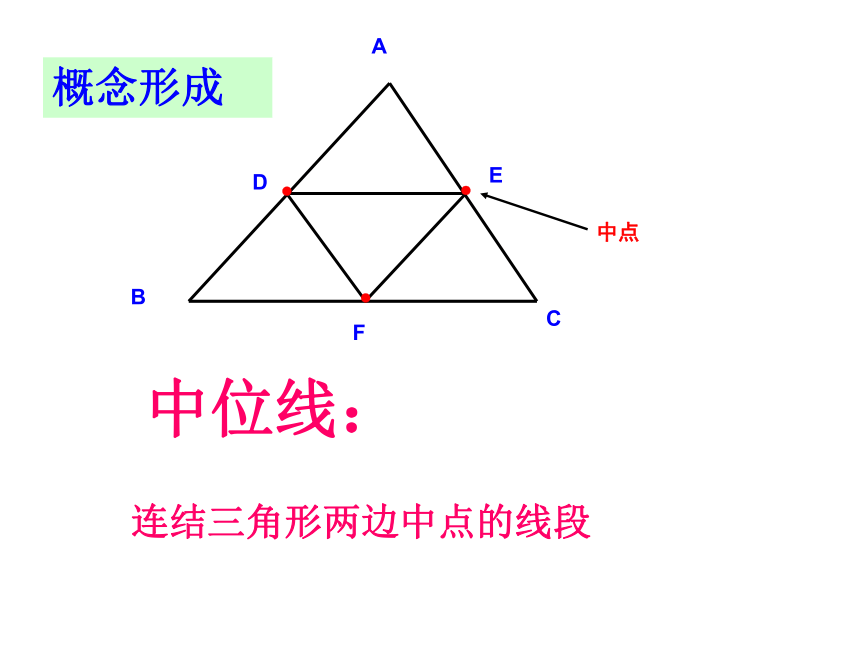
中位线:
连结三角形两边中点的线段
F
●
●
E
概念形成
三角形的中位线
连接三角形两边中点的线段叫做三角形的中位线。
画出三角形的所有中线并说出中位线和中线的区别.
D
E
F
获取新知
(1)相同之处——都和边的中点有关;
(2)不同之处:
三角形中位线的两个端点都是边的中点;
三角形中线只有一个端点是边的中点,另一端点是三角形的顶点。
概念对比
中线DC
中位线DE
DE和边BC关系
数量关系:
位置关系:
问题1:△ABC中,
中位线DE与BC存在何种关系?
合作探究
E
F
三角形的中位线平行于第三边,且等于第三边的一半.
几何语言:
①
证明平行问题
②
证明一条线段是另一条线段的两倍或一半
用
途
E
D
F
即时训练
练习1.如图,在△ABC中,D、E分别是AB、AC的中点
若∠ADE=65°,则∠B=
度,为什么?
若BC=8cm,则DE=
cm,为什么?
65
4
若AC=4cm,BC=6cm,AB=8cm,
则△DEF的周长=______
练习1.如图,在△ABC中,D、E、F分别是AB、AC、BC的中点
9cm
若△ABC的周长为24,△DEF的周长是_____
12
1、
三角形三条中位线围成的三角形的周长与原三角形的周长有什么关系?
合作探究
三角形三条中位线围成的三角形的周长是原三角形的周长的一半。
图中有_____个平行四边形
若△ABC的面积为24,△DEF的面积是_____
3
6
铁匠王师傅要把一块任意三角形铁皮,裁成四块形状大小完全
相同的小三角形铁皮,
你能帮助他想出办法吗?说说你
的想法。
链接生活
设
计
方
案:
F
(中点)
(中点)D
E(中点)
A
B
C
三角形面积的4等分:
A
B
C
测出MN的长,就可知A、B两点的距离
M
N
在AB外选一点C,使C能直接到达A和B,
连结AC和BC,并分别找出AC和BC的中点M、N.
若MN=36
m,则AB=
2MN=72
m
E,F是AB,BC的中点,你联想到什么?
要使EF成为一个三角形的中位线应怎样添加辅助线?
证明:如图,连接AC
∵EF是△ABC的中位线
同理得:
∴四边形EFGH是平行四边形
经典例题
答:
四边形EFGH为平行四边形。
例1
(1)?顺次连结任意四边形各边中点所得的四边形是什么图形?
平行四边形
已知:在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.求证∠1=∠2.
经典例题
例2
例3
求证三角形的一条中位线与第三边上的中线
互相平分.
已知:△ABC中,AD=DB,BE=EC,AF=FC.
求证:AE与DF互相平分.
E
证明:连接DE、EF,因为
AD=DB,BE=EC,
所以DE
∥AC(三角形的中位线平行于第三边并且等于第三边的一半)。
同理EF
∥AB。
所以四边形ADEF是平行四边形。
因此AE、DF互相平分。(平行四边形的对角线互相平分)
拓展提高
小结
1、三角形中位线的定义
2、三角形中位线定理
连接三角形两边中点的线段叫做三角形的中位线
三角形的中位线平行于三角形的第三边,且等于第三边的一半
基础练习:
1、已知三角形的各边长分别为6cm,8cm,12cm,
求连结各边中点所成三角形的周长__。
2、如果等边三角形的边长为3,那么连结各边中点
所成的三角形的周长__。
3、直角三角形两条直角边分别是6cm,8cm,
则连接着两条直角边中点的线段长为__。
13cm
4.5cm
5cm
《同步练习》
(五)、(六)
三角形的中位线
F
四边形BCFD是平行四边形吗?说说你的理由!
D
E
DE是三角形ABC的
中位线
获取新知
中位线:
连结三角形两边中点的线段
F
●
●
E
概念形成
三角形的中位线
连接三角形两边中点的线段叫做三角形的中位线。
画出三角形的所有中线并说出中位线和中线的区别.
D
E
F
获取新知
(1)相同之处——都和边的中点有关;
(2)不同之处:
三角形中位线的两个端点都是边的中点;
三角形中线只有一个端点是边的中点,另一端点是三角形的顶点。
概念对比
中线DC
中位线DE
DE和边BC关系
数量关系:
位置关系:
问题1:△ABC中,
中位线DE与BC存在何种关系?
合作探究
E
F
三角形的中位线平行于第三边,且等于第三边的一半.
几何语言:
①
证明平行问题
②
证明一条线段是另一条线段的两倍或一半
用
途
E
D
F
即时训练
练习1.如图,在△ABC中,D、E分别是AB、AC的中点
若∠ADE=65°,则∠B=
度,为什么?
若BC=8cm,则DE=
cm,为什么?
65
4
若AC=4cm,BC=6cm,AB=8cm,
则△DEF的周长=______
练习1.如图,在△ABC中,D、E、F分别是AB、AC、BC的中点
9cm
若△ABC的周长为24,△DEF的周长是_____
12
1、
三角形三条中位线围成的三角形的周长与原三角形的周长有什么关系?
合作探究
三角形三条中位线围成的三角形的周长是原三角形的周长的一半。
图中有_____个平行四边形
若△ABC的面积为24,△DEF的面积是_____
3
6
铁匠王师傅要把一块任意三角形铁皮,裁成四块形状大小完全
相同的小三角形铁皮,
你能帮助他想出办法吗?说说你
的想法。
链接生活
设
计
方
案:
F
(中点)
(中点)D
E(中点)
A
B
C
三角形面积的4等分:
A
B
C
测出MN的长,就可知A、B两点的距离
M
N
在AB外选一点C,使C能直接到达A和B,
连结AC和BC,并分别找出AC和BC的中点M、N.
若MN=36
m,则AB=
2MN=72
m
E,F是AB,BC的中点,你联想到什么?
要使EF成为一个三角形的中位线应怎样添加辅助线?
证明:如图,连接AC
∵EF是△ABC的中位线
同理得:
∴四边形EFGH是平行四边形
经典例题
答:
四边形EFGH为平行四边形。
例1
(1)?顺次连结任意四边形各边中点所得的四边形是什么图形?
平行四边形
已知:在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.求证∠1=∠2.
经典例题
例2
例3
求证三角形的一条中位线与第三边上的中线
互相平分.
已知:△ABC中,AD=DB,BE=EC,AF=FC.
求证:AE与DF互相平分.
E
证明:连接DE、EF,因为
AD=DB,BE=EC,
所以DE
∥AC(三角形的中位线平行于第三边并且等于第三边的一半)。
同理EF
∥AB。
所以四边形ADEF是平行四边形。
因此AE、DF互相平分。(平行四边形的对角线互相平分)
拓展提高
小结
1、三角形中位线的定义
2、三角形中位线定理
连接三角形两边中点的线段叫做三角形的中位线
三角形的中位线平行于三角形的第三边,且等于第三边的一半
基础练习:
1、已知三角形的各边长分别为6cm,8cm,12cm,
求连结各边中点所成三角形的周长__。
2、如果等边三角形的边长为3,那么连结各边中点
所成的三角形的周长__。
3、直角三角形两条直角边分别是6cm,8cm,
则连接着两条直角边中点的线段长为__。
13cm
4.5cm
5cm
《同步练习》
(五)、(六)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
