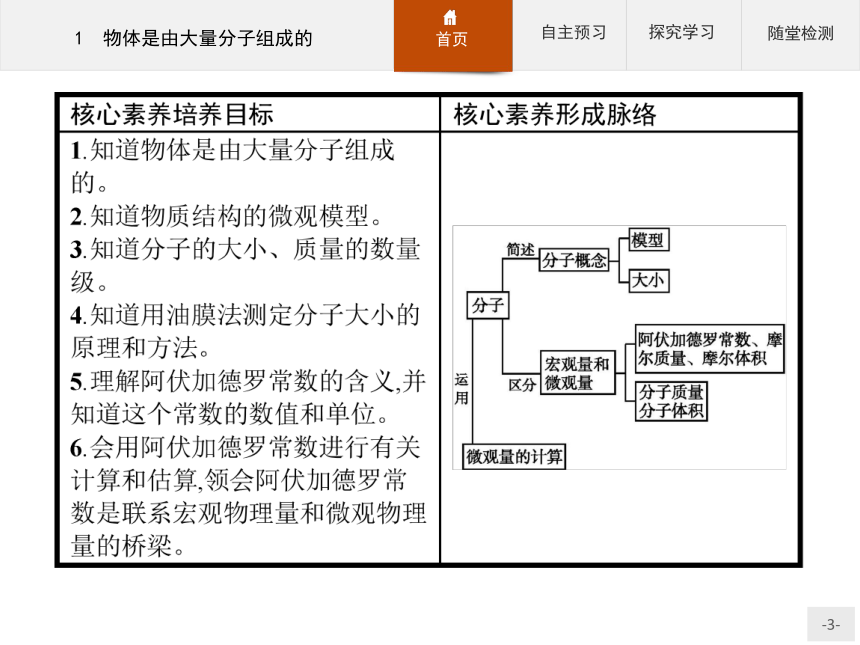
2020-2021物理人教版选修3-3课件:7.1 物体是由大量分子组成的34张含答案
文档属性
| 名称 | 2020-2021物理人教版选修3-3课件:7.1 物体是由大量分子组成的34张含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1019.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-06-03 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
第七章
分子动理论
1 物体是由大量分子组成的
一、分子的大小
1.估测分子直径采用什么方法?如何操作?
答案:油膜法。操作:把一滴油酸酒精溶液滴在水面上,在水面上就会形成油酸薄膜,薄膜是由单层的油酸分子组成的,尽管油酸分子有着复杂的结构和形状,但在估测其大小的数量级时,可以把它简化为球形(如图所示),油膜的厚度认为是油酸分子的直径d,测出油膜的面积S和体积V,则分子直径
2.分子大小的数量级:测量结果表明,除一些有机物质大分子外,多数分子的数量级为10-10
m。?
二、阿伏加德罗常数
1.定义:1
mol的任何物质都含有相同的粒子数,这个数量用阿伏加德罗常数表示。
2.数值:阿伏加德罗常数通常用符号NA表示,其值通常可取NA=6.02×1023
mol-1,在粗略计算中可取NA=6.0×1023
mol-1。?
3.意义:阿伏加德罗常数是一个重要的常数,它把摩尔质量、摩尔体积这些宏观量与分子质量、分子大小等微观量联系起来了。
(1)所有分子的直径都相同。( )
解析:多数分子直径的数量级都相同,均为10-10
m,但大小有差异。
答案:×
(2)油酸分子的形状是小球。( )
解析:分子有着复杂的内部结构,并不一定是小球,把分子看成小球,只是一种简化模型。
答案:×
(3)测定分子大小的方法有多种,油膜法只是其中的一种方法。(
)
解析:测定分子大小的方法还有显微法等其他方法,油膜法只是其中一种。
答案:√
自我检测
1.判断正误,对的画“√”,错的画“×”。
2.探究讨论。
(1)我们喝一口水大约喝下6.0×1023个水分子,如果动用全世界60亿人来数这些分子,每人每秒数一个,300万年也数不完,由此可见,分子大小的数量级很大还是很小?
答案:很小。
(2)1
mol氧气和1
mol水所含的粒子数相等吗?为什么?
答案:相等。因为1
mol氧气和1
mol水所含的粒子数都约是6.02×1023个。
(3)已知水的摩尔质量M=1.8×10-2
kg/mol,水分子的质量约为多少?
答案:由阿伏加德罗常数可知1
mol水中的分子数约为6.0×1023个,则每个水分子质量
探究一
探究二
油膜法估测分子的大小
问题探究
1.生活中,我们经常遇见这样一种现象,很少量的油不小心洒在水面上,将扩散很大的面积。为什么会出现这种现象呢?结合油膜法测分子直径,想一下为什么不能用纯油酸而是用酒精油酸溶液?
要点提示如果往水面上直接滴一滴纯油酸,那么它在水面上形成单分子油膜所需面积太大(大约几十平方米),实验室中很难提供这么大的容器,即使能提供,做起实验来也不方便。所以本实验中采取用酒精对油酸进行稀释的办法来获取更小体积的纯油酸,这样做更有利于油酸在水面上形成单分子油膜。同时酒精易挥发,不影响测量结果。
2.实验中为什么在水面上撒痱子粉(或细石膏粉)?
要点提示撒痱子粉或细石膏粉的目的是为了方便观察、描绘所形成油膜的轮廓。
探究一
探究二
知识归纳
1.油膜法估测分子大小中的“两测一算”
(1)测量一滴油酸酒精溶液中纯油酸的体积。
先配制一定浓度的油酸酒精溶液,用注射器或滴管将事先配制好的油酸酒精溶液一滴一滴地滴入量筒中,记下量筒内增加一定体积(例如1
mL)时的滴数,从而可算出一滴溶液的体积,再结合溶液的浓度就可以计算出一滴溶液中所含纯油酸的体积。
(2)测量单分子油膜的面积。
①在浅盘中装入2
cm深的水,然后将痱子粉或细石膏粉均匀地撒在水面上。
②将一滴油酸酒精溶液滴在水面上,待油酸薄膜的形状稳定后,将玻璃板放在浅盘上,用彩笔将薄膜的形状描画在玻璃板上。
探究一
探究二
③将画有油膜轮廓的玻璃板放在坐标纸上,数出轮廓内的方格数(不足半个的舍去,多于半个的算一个),再根据方格的个数求出油膜的面积S。
(3)估算分子的直径。
如果一滴油酸酒精溶液中纯油酸的体积为V,所形成的单分子油膜的面积为S,则分子的直径为
探究一
探究二
2.油膜法估测分子大小中的注意事项
(1)油酸酒精溶液配制后不要长时间放置,以免浓度改变,产生较大的实验误差。
(2)实验前应注意,方盘应该干净,否则难以形成油膜。
(3)痱子粉的用量不要太多,否则不易成功。撒完后,方盘中的水面应保持平衡,痱子粉应均匀浮在水面上。
(4)向水面滴一滴油酸酒精溶液。
(5)滴油酸酒精溶液的滴口应在离水面1
cm之内,否则油膜难以形成。
(6)要待油膜形状稳定后,再画轮廓。
(7)运用数格子法测油膜面积。多于半个的算一个,少于半个的舍去。这种方法所取方格的单位越小,计算的面积误差越小。
(8)本实验只要求估算分子大小,实验结果数量级符合要求即可。
探究一
探究二
典例剖析
【例题1】
在做用油膜法估测分子大小的实验中,油酸酒精溶液的浓度为每104
mL的溶液中有纯油酸6
mL。用注射器测得1
mL上述溶液中有液滴50滴。把1滴该溶液滴入盛水的浅盘里,待水面稳定后,将玻璃板放在浅盘上,在玻璃板上描出油膜的轮廓,然后把玻璃板放在坐标纸上,其形状如图所示,坐标中正方形小方格的边长为20
mm。求:
(1)油酸膜的面积是多少?
(2)每一滴油酸酒精溶液中含有纯油酸的体积
是多少?
(3)根据上述数据,估测出油酸分子的直径是多少?(结果保留两位有效数字)
探究一
探究二
【思考问题】
(1)怎样根据油膜形状求油膜的面积?
提示先数出坐标纸上方格的个数,然后求出油膜的面积。
(2)怎样求解一滴油酸酒精溶液所含纯油酸的体积?
提示一滴溶液的体积乘以溶液的浓度,就是一滴油酸酒精溶液所含纯油酸的体积。
探究一
探究二
解析:(1)用填补法数出在油膜轮廓内的格数(面积大于半个方格的算一个,不足半格的舍去不算)约为58个,油膜面积为S=58×(20×10-3
m)2=2.32×10-2
m2。
(2)因50滴油酸酒精溶液的体积为1
mL,且溶液含纯油酸的浓度为ρ=0.06%,故每滴油酸酒精溶液含纯油酸的体积为
(3)把油酸薄膜的厚度视为油酸分子的直径,可估算出油酸分子的直径为
答案:(1)2.32×10-2
m2 (2)1.2×10-11
m3 (3)5.2×10-10
m
探究一
探究二
油膜法估测分子直径,关键是获得一滴油酸酒精溶液,并由配制浓度求出其中所含纯油酸的体积,再就是用数格子法(对外围小格采用“填补法”即“四舍五入”法)求出油膜面积,再由公式
探究一
探究二
变式训练1在油膜法估测油酸分子的大小实验中,有下列实验步骤:
①往边长约为40
cm的浅盘里倒入约2
cm深的水,待水面稳定后将适量的痱子粉均匀地撒在水面上。
②用注射器将事先配好的油酸酒精溶液滴一滴在水面上,待薄膜形状稳定。
③将画有油膜形状的玻璃板平放在坐标纸上,计算出油膜的面积,根据油酸的体积和面积计算出油酸分子直径的大小。
④用注射器将事先配好的油酸酒精溶液一滴一滴地滴入量筒中,记下量筒内每增加一定体积时的滴数,由此计算出一滴油酸酒精溶液的体积。
⑤将玻璃板放在浅盘上,然后将油膜的形状用彩笔描绘在玻璃板上。
探究一
探究二
完成下列填空:
(1)上述步骤中,正确的顺序是 (填写步骤前面的数字)。?
(2)将1
cm3的油酸溶于酒精,制成300
cm3的油酸酒精溶液,测得1
cm3的油酸酒精溶液有50滴。现取1滴该油酸酒精溶液滴在水面上,测得所形成的油膜的面积是0.13
m2。由此估算出油酸分子的直径为
m(结果保留一位有效数字)。?
解析:(1)在油膜法估测油酸分子的大小实验中,应先配制油酸酒精溶液,再往盘中倒入水,并撒痱子粉,然后用注射器将配好的溶液滴一滴在水面上,待油膜形状稳定,再将玻璃板放于盘上,用彩笔描绘在玻璃板上,根据
计算。
答案:(1)④①②⑤③ (2)5×10-10
m
探究一
探究二
阿伏加德罗常数
问题探究
如图所示为某购物网站出售的某地的新鲜空气,成年人做一次深呼吸,大约吸入450
cm3的空气,如果在标准状况下,该体积的空气物质的量是多少?大约含有多少个分子?
要点提示成年人做一次深呼吸吸入空气的物质的量
≈0.02
mol。大约含有的分子数N=nNA=0.02
mol×6.02×1023
mol-1≈1.2×1022(个)。
探究一
探究二
知识归纳
1.阿伏加德罗常数的应用
设物质(固体或液体)的摩尔质量为M(kg/mol),摩尔体积为Vm(m3/mol),物体的质量为m(kg),体积为V(m3),密度为ρ(kg/m3),该物质1个分子的体积为V0(m3),一个分子的质量为m0(kg),则:
探究一
探究二
探究一
探究二
2.对分子模型的理解
(1)球形模型:
固体和液体可看作一个紧挨着一个的球形分子排列而成,忽略分子间空隙,如图甲所示。
(2)立方体模型:
气体分子间的空隙很大,把气体分成若干个小立方体,气体分子位于每个小立方体的中心,每个小立方体是每个分子平均占有的活动空间,忽略气体分子的大小,如图乙所示。
探究一
探究二
(3)分子大小的估算:
①对于固体和液体,分子间距离比较小,可以认为分子是一个个
②对于气体,分子间距离比较大,处理方法是把气体分子所占据的空间视为立方体模型,从而可计算出两气体分子之间的平均间距
建立的模型不同,得出的结果会稍有不同,但数量级一般是相同的。一般在估算固体或液体分子直径或分子间距离时采用球形模型,而在估算气体分子间的距离时采用立方体模型。
探究一
探究二
典例剖析
【例题2】
若以M表示水的摩尔质量,Vm表示在标准状态下水蒸气的摩尔体积,ρ为在标准状态下水蒸气的密度,NA为阿伏加德罗常数,m0、V0分别表示每个水分子的质量和体积,下面四个关系式:
其中正确的是( )
A.①和② B.①和③
C.③和④
D.①和④
【思考问题】
(1)如何处理固体与液体间的分子间隙?
提示固体与液体间的分子间隙较小,可以忽略不计。
(2)摩尔质量、密度、摩尔体积三者有什么关系?
提示摩尔质量等于密度乘以摩尔体积。
探究一
探究二
求出的是一个气体分子平均占有的空间,一个气体分子的体积远远小于该空间,所以④式不正确。②式中V0是每个分子的体积,不是每个分子所占的体积,这样算不出气体密度,故②式也不正确。
答案:B
分子动理论中宏观量与微观量之间的关系
由宏观量计算微观量,或由微观量计算宏观量,都要通过阿伏加德罗常数建立联系。所以说,阿伏加德罗常数是联系宏观量与微观量的桥梁。
探究一
探究二
变式训练2(多选)能根据下列一组数据算出阿伏加德罗常数的是( )
A.氧气的摩尔质量、氧气分子的质量
B.水的摩尔质量、水的密度及水分子的直径
C.氧气的摩尔质量、氧气的密度及氧气分子的直径
D.水分子的质量和一杯水的质量、体积
探究一
探究二
答案:AB
1
2
3
4
5
1.(多选)用油膜法估测分子直径的理想条件是
( )
A.将油酸分子看成球体
B.考虑各油酸分子间的间隙
C.认为油酸分子是紧密排列的
D.将油膜看成单分子油膜
解析:用油膜法测油酸分子直径的三个前提条件:①将油酸分子视为球体模型;②忽略油酸分子之间的间隙,认为分子是紧密排列的;③油酸分子在水面是单分子排列。只有在上述三个理想条件下油酸的厚度才能视为油酸分子的直径。
答案:ACD
1
2
3
4
5
2.(多选)关于分子,下列说法正确的是( )
A.分子看作球体是对分子的简化模型,实际上,分子的形状并不真的都是球体
B.不同分子的直径一般不同,但数量级一定相同,均为10-10
m
C.在计算分子间距时,固体、液体、气体分子均可看作一个挨一个紧密排列,且均可视为球体模型
D.对于固体、液体,可较易估算出其分子间距或分子直径,但对于气体,一般不能估算出分子直径,只能估算分子间距
1
2
3
4
5
解析:实际上,分子的结构非常复杂,它的形状并不真的都是小球,分子直径不可能都相同,除一些有机大分子外,一般分子直径的数量级为10-10
m。在计算分子直径时,由于固体、液体分子间距较小,可认为分子是一个挨一个紧密排列的,分子可看作球体或正方体,分子间距即为分子直径大小。但对于气体,由于分子间距比其分子直径大得多,不能认为一个挨一个紧密排列,一般只能估算分子间距,不能估算其直径,且估算分子间距时,气体分子所占据的空间应看作立方体。
答案:AD
1
2
3
4
5
3.美丽的“水立方”游泳馆是很好的体育场馆,但“水立方”同时也是公认的耗水大户,因此,“水立方”专门设计了雨水回收系统,平均每年可以回收雨水10
500
m3,相当于100户居民一年的用水量,请你根据上述数据估算一户居民一天的平均用水量与下面哪个水分子数目最接近(设水分子的摩尔质量为M=1.8×10-2
kg/mol)
( )
A.3×1031个
B.3×1028个
C.9×1027个
D.9×1030个
答案:C
1
2
3
4
5
4.
对于液体和固体来说,如果用M表示摩尔质量,m0表示分子质量,ρ表示物质的密度,Vm表示摩尔体积,V0表示分子体积,NA表示阿伏加德罗常数,下列关系正确的是( )
解析:摩尔体积是1
mol分子的体积,故
,故A正确,B错误;摩尔质量等于密度乘以摩尔体积,M=ρVm,故C、D错误。
答案:A
1
2
3
4
5
5.我们知道被动吸烟比主动吸烟害处更大。一个高约2.8
m、面积约10
m2的办公室,若只有一人吸了一根烟呼出的烟气均匀分布在办公室内。(人正常呼吸一次吸入气体300
cm3,一根烟大约吸10次)
(1)估算被污染的空气分子间的平均距离;
(2)另一不吸烟者一次呼吸大约吸入多少个被污染过的空气分子?
1
2
3
4
5
(2)被动吸烟者一次吸入被污染的空气分子数为
N″=2.9×1021×300×10-6个=8.7×1017个。
答案:(1)7×10-8
m (2)8.7×1017个
第七章
分子动理论
1 物体是由大量分子组成的
一、分子的大小
1.估测分子直径采用什么方法?如何操作?
答案:油膜法。操作:把一滴油酸酒精溶液滴在水面上,在水面上就会形成油酸薄膜,薄膜是由单层的油酸分子组成的,尽管油酸分子有着复杂的结构和形状,但在估测其大小的数量级时,可以把它简化为球形(如图所示),油膜的厚度认为是油酸分子的直径d,测出油膜的面积S和体积V,则分子直径
2.分子大小的数量级:测量结果表明,除一些有机物质大分子外,多数分子的数量级为10-10
m。?
二、阿伏加德罗常数
1.定义:1
mol的任何物质都含有相同的粒子数,这个数量用阿伏加德罗常数表示。
2.数值:阿伏加德罗常数通常用符号NA表示,其值通常可取NA=6.02×1023
mol-1,在粗略计算中可取NA=6.0×1023
mol-1。?
3.意义:阿伏加德罗常数是一个重要的常数,它把摩尔质量、摩尔体积这些宏观量与分子质量、分子大小等微观量联系起来了。
(1)所有分子的直径都相同。( )
解析:多数分子直径的数量级都相同,均为10-10
m,但大小有差异。
答案:×
(2)油酸分子的形状是小球。( )
解析:分子有着复杂的内部结构,并不一定是小球,把分子看成小球,只是一种简化模型。
答案:×
(3)测定分子大小的方法有多种,油膜法只是其中的一种方法。(
)
解析:测定分子大小的方法还有显微法等其他方法,油膜法只是其中一种。
答案:√
自我检测
1.判断正误,对的画“√”,错的画“×”。
2.探究讨论。
(1)我们喝一口水大约喝下6.0×1023个水分子,如果动用全世界60亿人来数这些分子,每人每秒数一个,300万年也数不完,由此可见,分子大小的数量级很大还是很小?
答案:很小。
(2)1
mol氧气和1
mol水所含的粒子数相等吗?为什么?
答案:相等。因为1
mol氧气和1
mol水所含的粒子数都约是6.02×1023个。
(3)已知水的摩尔质量M=1.8×10-2
kg/mol,水分子的质量约为多少?
答案:由阿伏加德罗常数可知1
mol水中的分子数约为6.0×1023个,则每个水分子质量
探究一
探究二
油膜法估测分子的大小
问题探究
1.生活中,我们经常遇见这样一种现象,很少量的油不小心洒在水面上,将扩散很大的面积。为什么会出现这种现象呢?结合油膜法测分子直径,想一下为什么不能用纯油酸而是用酒精油酸溶液?
要点提示如果往水面上直接滴一滴纯油酸,那么它在水面上形成单分子油膜所需面积太大(大约几十平方米),实验室中很难提供这么大的容器,即使能提供,做起实验来也不方便。所以本实验中采取用酒精对油酸进行稀释的办法来获取更小体积的纯油酸,这样做更有利于油酸在水面上形成单分子油膜。同时酒精易挥发,不影响测量结果。
2.实验中为什么在水面上撒痱子粉(或细石膏粉)?
要点提示撒痱子粉或细石膏粉的目的是为了方便观察、描绘所形成油膜的轮廓。
探究一
探究二
知识归纳
1.油膜法估测分子大小中的“两测一算”
(1)测量一滴油酸酒精溶液中纯油酸的体积。
先配制一定浓度的油酸酒精溶液,用注射器或滴管将事先配制好的油酸酒精溶液一滴一滴地滴入量筒中,记下量筒内增加一定体积(例如1
mL)时的滴数,从而可算出一滴溶液的体积,再结合溶液的浓度就可以计算出一滴溶液中所含纯油酸的体积。
(2)测量单分子油膜的面积。
①在浅盘中装入2
cm深的水,然后将痱子粉或细石膏粉均匀地撒在水面上。
②将一滴油酸酒精溶液滴在水面上,待油酸薄膜的形状稳定后,将玻璃板放在浅盘上,用彩笔将薄膜的形状描画在玻璃板上。
探究一
探究二
③将画有油膜轮廓的玻璃板放在坐标纸上,数出轮廓内的方格数(不足半个的舍去,多于半个的算一个),再根据方格的个数求出油膜的面积S。
(3)估算分子的直径。
如果一滴油酸酒精溶液中纯油酸的体积为V,所形成的单分子油膜的面积为S,则分子的直径为
探究一
探究二
2.油膜法估测分子大小中的注意事项
(1)油酸酒精溶液配制后不要长时间放置,以免浓度改变,产生较大的实验误差。
(2)实验前应注意,方盘应该干净,否则难以形成油膜。
(3)痱子粉的用量不要太多,否则不易成功。撒完后,方盘中的水面应保持平衡,痱子粉应均匀浮在水面上。
(4)向水面滴一滴油酸酒精溶液。
(5)滴油酸酒精溶液的滴口应在离水面1
cm之内,否则油膜难以形成。
(6)要待油膜形状稳定后,再画轮廓。
(7)运用数格子法测油膜面积。多于半个的算一个,少于半个的舍去。这种方法所取方格的单位越小,计算的面积误差越小。
(8)本实验只要求估算分子大小,实验结果数量级符合要求即可。
探究一
探究二
典例剖析
【例题1】
在做用油膜法估测分子大小的实验中,油酸酒精溶液的浓度为每104
mL的溶液中有纯油酸6
mL。用注射器测得1
mL上述溶液中有液滴50滴。把1滴该溶液滴入盛水的浅盘里,待水面稳定后,将玻璃板放在浅盘上,在玻璃板上描出油膜的轮廓,然后把玻璃板放在坐标纸上,其形状如图所示,坐标中正方形小方格的边长为20
mm。求:
(1)油酸膜的面积是多少?
(2)每一滴油酸酒精溶液中含有纯油酸的体积
是多少?
(3)根据上述数据,估测出油酸分子的直径是多少?(结果保留两位有效数字)
探究一
探究二
【思考问题】
(1)怎样根据油膜形状求油膜的面积?
提示先数出坐标纸上方格的个数,然后求出油膜的面积。
(2)怎样求解一滴油酸酒精溶液所含纯油酸的体积?
提示一滴溶液的体积乘以溶液的浓度,就是一滴油酸酒精溶液所含纯油酸的体积。
探究一
探究二
解析:(1)用填补法数出在油膜轮廓内的格数(面积大于半个方格的算一个,不足半格的舍去不算)约为58个,油膜面积为S=58×(20×10-3
m)2=2.32×10-2
m2。
(2)因50滴油酸酒精溶液的体积为1
mL,且溶液含纯油酸的浓度为ρ=0.06%,故每滴油酸酒精溶液含纯油酸的体积为
(3)把油酸薄膜的厚度视为油酸分子的直径,可估算出油酸分子的直径为
答案:(1)2.32×10-2
m2 (2)1.2×10-11
m3 (3)5.2×10-10
m
探究一
探究二
油膜法估测分子直径,关键是获得一滴油酸酒精溶液,并由配制浓度求出其中所含纯油酸的体积,再就是用数格子法(对外围小格采用“填补法”即“四舍五入”法)求出油膜面积,再由公式
探究一
探究二
变式训练1在油膜法估测油酸分子的大小实验中,有下列实验步骤:
①往边长约为40
cm的浅盘里倒入约2
cm深的水,待水面稳定后将适量的痱子粉均匀地撒在水面上。
②用注射器将事先配好的油酸酒精溶液滴一滴在水面上,待薄膜形状稳定。
③将画有油膜形状的玻璃板平放在坐标纸上,计算出油膜的面积,根据油酸的体积和面积计算出油酸分子直径的大小。
④用注射器将事先配好的油酸酒精溶液一滴一滴地滴入量筒中,记下量筒内每增加一定体积时的滴数,由此计算出一滴油酸酒精溶液的体积。
⑤将玻璃板放在浅盘上,然后将油膜的形状用彩笔描绘在玻璃板上。
探究一
探究二
完成下列填空:
(1)上述步骤中,正确的顺序是 (填写步骤前面的数字)。?
(2)将1
cm3的油酸溶于酒精,制成300
cm3的油酸酒精溶液,测得1
cm3的油酸酒精溶液有50滴。现取1滴该油酸酒精溶液滴在水面上,测得所形成的油膜的面积是0.13
m2。由此估算出油酸分子的直径为
m(结果保留一位有效数字)。?
解析:(1)在油膜法估测油酸分子的大小实验中,应先配制油酸酒精溶液,再往盘中倒入水,并撒痱子粉,然后用注射器将配好的溶液滴一滴在水面上,待油膜形状稳定,再将玻璃板放于盘上,用彩笔描绘在玻璃板上,根据
计算。
答案:(1)④①②⑤③ (2)5×10-10
m
探究一
探究二
阿伏加德罗常数
问题探究
如图所示为某购物网站出售的某地的新鲜空气,成年人做一次深呼吸,大约吸入450
cm3的空气,如果在标准状况下,该体积的空气物质的量是多少?大约含有多少个分子?
要点提示成年人做一次深呼吸吸入空气的物质的量
≈0.02
mol。大约含有的分子数N=nNA=0.02
mol×6.02×1023
mol-1≈1.2×1022(个)。
探究一
探究二
知识归纳
1.阿伏加德罗常数的应用
设物质(固体或液体)的摩尔质量为M(kg/mol),摩尔体积为Vm(m3/mol),物体的质量为m(kg),体积为V(m3),密度为ρ(kg/m3),该物质1个分子的体积为V0(m3),一个分子的质量为m0(kg),则:
探究一
探究二
探究一
探究二
2.对分子模型的理解
(1)球形模型:
固体和液体可看作一个紧挨着一个的球形分子排列而成,忽略分子间空隙,如图甲所示。
(2)立方体模型:
气体分子间的空隙很大,把气体分成若干个小立方体,气体分子位于每个小立方体的中心,每个小立方体是每个分子平均占有的活动空间,忽略气体分子的大小,如图乙所示。
探究一
探究二
(3)分子大小的估算:
①对于固体和液体,分子间距离比较小,可以认为分子是一个个
②对于气体,分子间距离比较大,处理方法是把气体分子所占据的空间视为立方体模型,从而可计算出两气体分子之间的平均间距
建立的模型不同,得出的结果会稍有不同,但数量级一般是相同的。一般在估算固体或液体分子直径或分子间距离时采用球形模型,而在估算气体分子间的距离时采用立方体模型。
探究一
探究二
典例剖析
【例题2】
若以M表示水的摩尔质量,Vm表示在标准状态下水蒸气的摩尔体积,ρ为在标准状态下水蒸气的密度,NA为阿伏加德罗常数,m0、V0分别表示每个水分子的质量和体积,下面四个关系式:
其中正确的是( )
A.①和② B.①和③
C.③和④
D.①和④
【思考问题】
(1)如何处理固体与液体间的分子间隙?
提示固体与液体间的分子间隙较小,可以忽略不计。
(2)摩尔质量、密度、摩尔体积三者有什么关系?
提示摩尔质量等于密度乘以摩尔体积。
探究一
探究二
求出的是一个气体分子平均占有的空间,一个气体分子的体积远远小于该空间,所以④式不正确。②式中V0是每个分子的体积,不是每个分子所占的体积,这样算不出气体密度,故②式也不正确。
答案:B
分子动理论中宏观量与微观量之间的关系
由宏观量计算微观量,或由微观量计算宏观量,都要通过阿伏加德罗常数建立联系。所以说,阿伏加德罗常数是联系宏观量与微观量的桥梁。
探究一
探究二
变式训练2(多选)能根据下列一组数据算出阿伏加德罗常数的是( )
A.氧气的摩尔质量、氧气分子的质量
B.水的摩尔质量、水的密度及水分子的直径
C.氧气的摩尔质量、氧气的密度及氧气分子的直径
D.水分子的质量和一杯水的质量、体积
探究一
探究二
答案:AB
1
2
3
4
5
1.(多选)用油膜法估测分子直径的理想条件是
( )
A.将油酸分子看成球体
B.考虑各油酸分子间的间隙
C.认为油酸分子是紧密排列的
D.将油膜看成单分子油膜
解析:用油膜法测油酸分子直径的三个前提条件:①将油酸分子视为球体模型;②忽略油酸分子之间的间隙,认为分子是紧密排列的;③油酸分子在水面是单分子排列。只有在上述三个理想条件下油酸的厚度才能视为油酸分子的直径。
答案:ACD
1
2
3
4
5
2.(多选)关于分子,下列说法正确的是( )
A.分子看作球体是对分子的简化模型,实际上,分子的形状并不真的都是球体
B.不同分子的直径一般不同,但数量级一定相同,均为10-10
m
C.在计算分子间距时,固体、液体、气体分子均可看作一个挨一个紧密排列,且均可视为球体模型
D.对于固体、液体,可较易估算出其分子间距或分子直径,但对于气体,一般不能估算出分子直径,只能估算分子间距
1
2
3
4
5
解析:实际上,分子的结构非常复杂,它的形状并不真的都是小球,分子直径不可能都相同,除一些有机大分子外,一般分子直径的数量级为10-10
m。在计算分子直径时,由于固体、液体分子间距较小,可认为分子是一个挨一个紧密排列的,分子可看作球体或正方体,分子间距即为分子直径大小。但对于气体,由于分子间距比其分子直径大得多,不能认为一个挨一个紧密排列,一般只能估算分子间距,不能估算其直径,且估算分子间距时,气体分子所占据的空间应看作立方体。
答案:AD
1
2
3
4
5
3.美丽的“水立方”游泳馆是很好的体育场馆,但“水立方”同时也是公认的耗水大户,因此,“水立方”专门设计了雨水回收系统,平均每年可以回收雨水10
500
m3,相当于100户居民一年的用水量,请你根据上述数据估算一户居民一天的平均用水量与下面哪个水分子数目最接近(设水分子的摩尔质量为M=1.8×10-2
kg/mol)
( )
A.3×1031个
B.3×1028个
C.9×1027个
D.9×1030个
答案:C
1
2
3
4
5
4.
对于液体和固体来说,如果用M表示摩尔质量,m0表示分子质量,ρ表示物质的密度,Vm表示摩尔体积,V0表示分子体积,NA表示阿伏加德罗常数,下列关系正确的是( )
解析:摩尔体积是1
mol分子的体积,故
,故A正确,B错误;摩尔质量等于密度乘以摩尔体积,M=ρVm,故C、D错误。
答案:A
1
2
3
4
5
5.我们知道被动吸烟比主动吸烟害处更大。一个高约2.8
m、面积约10
m2的办公室,若只有一人吸了一根烟呼出的烟气均匀分布在办公室内。(人正常呼吸一次吸入气体300
cm3,一根烟大约吸10次)
(1)估算被污染的空气分子间的平均距离;
(2)另一不吸烟者一次呼吸大约吸入多少个被污染过的空气分子?
1
2
3
4
5
(2)被动吸烟者一次吸入被污染的空气分子数为
N″=2.9×1021×300×10-6个=8.7×1017个。
答案:(1)7×10-8
m (2)8.7×1017个
