山东省东平县实验中学2019-2020学年六年级下数学9.2用关系式表示变量之间的关系课件(20张ppt)
文档属性
| 名称 | 山东省东平县实验中学2019-2020学年六年级下数学9.2用关系式表示变量之间的关系课件(20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 577.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-03 10:34:14 | ||
图片预览




文档简介
(共20张PPT)
9.2用表达式表示变量之间的关系2
鲁教版六年级下册数学课件
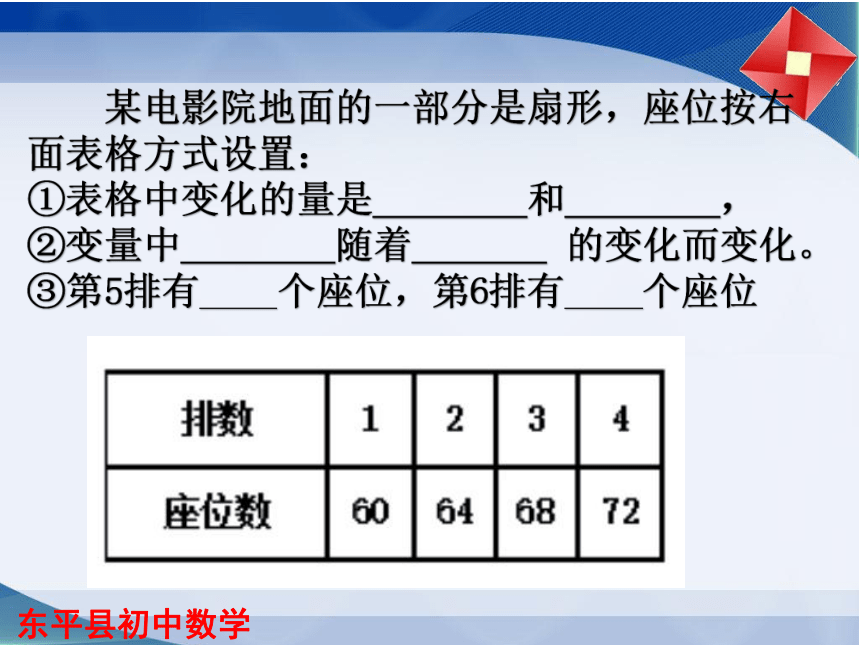
某电影院地面的一部分是扇形,座位按右面表格方式设置:
①表格中变化的量是
和
,
②变量中
随着
的变化而变化。
③第5排有____个座位,第6排有____个座位
1.如果△ABC的底边长为a,为h
,
那么面积
S△ABC
=_____________.2.如果梯形的上底、下底长分别为a、b,
高为h
,
那么面积
S梯形=_____________.3.如果圆的半径为r,
那么圆的面积
S=
.4.如果圆锥底面的半径为r,高为h,
体积V圆锥=_______________.
学习目标
1.了解表达式是表示变量之间关系的另一种方法;
2.探索具体问题中变量间的关系,并能用表达式表示出来.
3.能根据表达式求值,初步体会自变量和因变量的数值对应关系。
4.进一步发展符号感、初步感受模型思想。
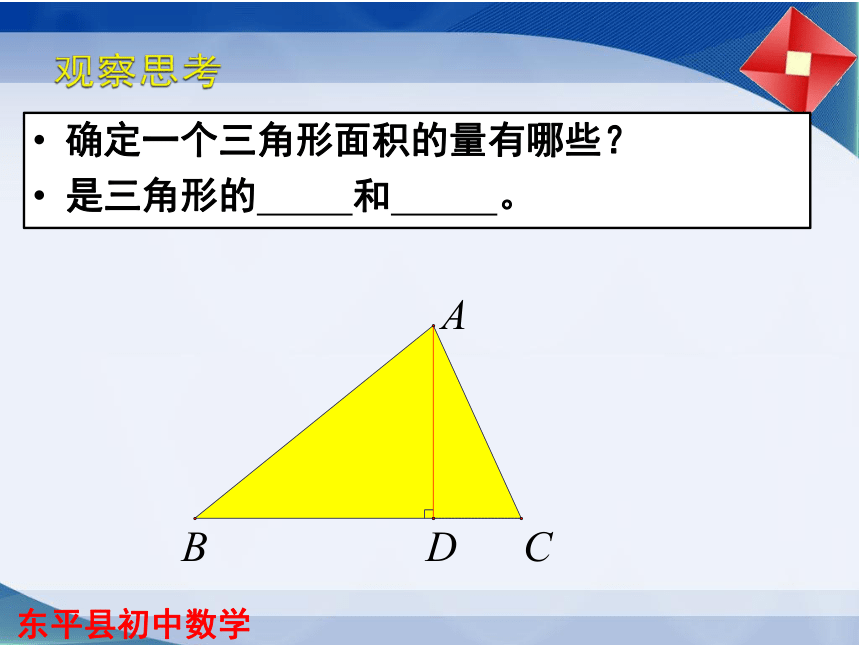
确定一个三角形面积的量有哪些?
是三角形的
和
。
D
B
C
A
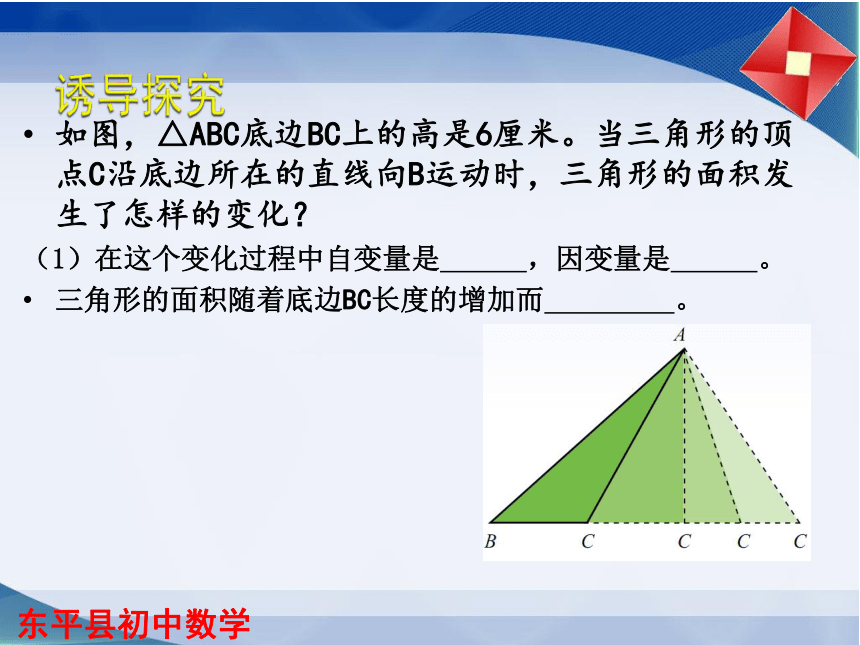
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在的直线向B运动时,三角形的面积发生了怎样的变化?
(1)在这个变化过程中自变量是
,因变量是
。
三角形的面积随着底边BC长度的增加而
。
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在的直线向B运动时,三角形的面积发生了怎样的变化?
(2)如果三角形的底边长为x(厘米),
那么三角形的面积y(平方厘米)可以表示为_________。
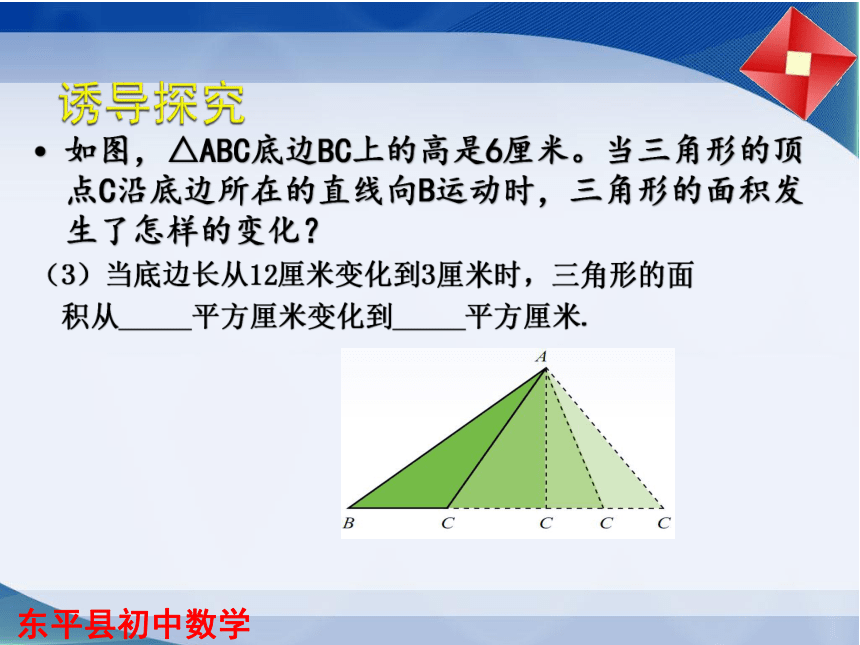
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在的直线向B运动时,三角形的面积发生了怎样的变化?
(3)当底边长从12厘米变化到3厘米时,三角形的面
积从_____平方厘米变化到_____平方厘米.
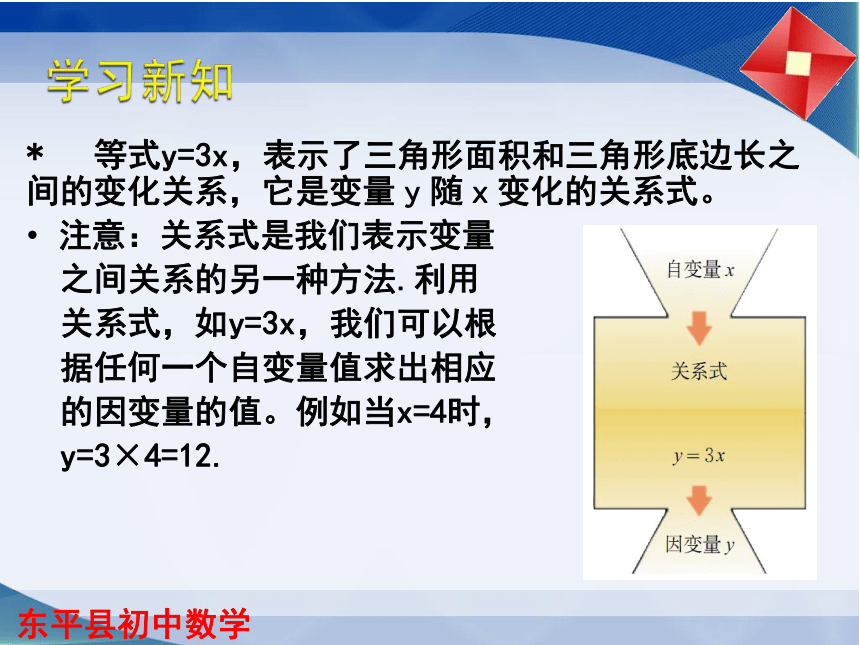
等式y=3x,表示了三角形面积和三角形底边长之间的变化关系,它是变量y随x变化的关系式。
注意:关系式是我们表示变量
之间关系的另一种方法.利用
关系式,如y=3x,我们可以根
据任何一个自变量值求出相应
的因变量的值。例如当x=4时,
y=3×4=12.
你还记得圆锥的体积公式是什么吗?
其中的字母表示什么?
如图,圆锥的高度是4厘米,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化。
(1)在这个变化过程中,自变量、因变量各是什么?
如图,圆锥的高度是4厘米,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化。
(2)如果圆锥底面半径为
r(厘米),那么圆锥的体积v(厘米3)与r的关系式为:
______________
议一议:
你知道什么是“低碳生活”吗?“低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳、特别是二氧化碳的排放量的一种方式。
议一议:
(1)如果家居用电的二氧化碳排放量用y表示,耗电量用x表示,那么y与x之间的关系式可以表示为_____________。
议一议:
(2)在上述关系式中,耗电量每增加1
KW·h,二氧化碳排放量增加___________。当耗电量从1
KW·h增加到100KW·h时,二氧化碳排放量从____
___增加到_____________。
议一议:
(3)小明家本月用电大约110
KW·h、天然气20m3、自来水5t、油耗75L,请你计算一下小明家这几
项的二氧化碳排放量。
1、在地球某地,温度T(℃)与高度d(m)的关系可以
近似地用
来表示,
根据这个关系式,当d的值分别是200,400,600,800,1000时,计算相应的T值,并用表格表示所得结果。
2.如图所示,长方形的长为12,宽为x,则:
①设长方形面积S,写出S与x的关系式。
②若用C表示长方形的周长,写出周长C与宽x之间的关系式。
说说,你有哪些
收获和困惑?
畅所欲言
谢谢聆听!
9.2用表达式表示变量之间的关系2
鲁教版六年级下册数学课件
某电影院地面的一部分是扇形,座位按右面表格方式设置:
①表格中变化的量是
和
,
②变量中
随着
的变化而变化。
③第5排有____个座位,第6排有____个座位
1.如果△ABC的底边长为a,为h
,
那么面积
S△ABC
=_____________.2.如果梯形的上底、下底长分别为a、b,
高为h
,
那么面积
S梯形=_____________.3.如果圆的半径为r,
那么圆的面积
S=
.4.如果圆锥底面的半径为r,高为h,
体积V圆锥=_______________.
学习目标
1.了解表达式是表示变量之间关系的另一种方法;
2.探索具体问题中变量间的关系,并能用表达式表示出来.
3.能根据表达式求值,初步体会自变量和因变量的数值对应关系。
4.进一步发展符号感、初步感受模型思想。
确定一个三角形面积的量有哪些?
是三角形的
和
。
D
B
C
A
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在的直线向B运动时,三角形的面积发生了怎样的变化?
(1)在这个变化过程中自变量是
,因变量是
。
三角形的面积随着底边BC长度的增加而
。
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在的直线向B运动时,三角形的面积发生了怎样的变化?
(2)如果三角形的底边长为x(厘米),
那么三角形的面积y(平方厘米)可以表示为_________。
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在的直线向B运动时,三角形的面积发生了怎样的变化?
(3)当底边长从12厘米变化到3厘米时,三角形的面
积从_____平方厘米变化到_____平方厘米.
等式y=3x,表示了三角形面积和三角形底边长之间的变化关系,它是变量y随x变化的关系式。
注意:关系式是我们表示变量
之间关系的另一种方法.利用
关系式,如y=3x,我们可以根
据任何一个自变量值求出相应
的因变量的值。例如当x=4时,
y=3×4=12.
你还记得圆锥的体积公式是什么吗?
其中的字母表示什么?
如图,圆锥的高度是4厘米,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化。
(1)在这个变化过程中,自变量、因变量各是什么?
如图,圆锥的高度是4厘米,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化。
(2)如果圆锥底面半径为
r(厘米),那么圆锥的体积v(厘米3)与r的关系式为:
______________
议一议:
你知道什么是“低碳生活”吗?“低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳、特别是二氧化碳的排放量的一种方式。
议一议:
(1)如果家居用电的二氧化碳排放量用y表示,耗电量用x表示,那么y与x之间的关系式可以表示为_____________。
议一议:
(2)在上述关系式中,耗电量每增加1
KW·h,二氧化碳排放量增加___________。当耗电量从1
KW·h增加到100KW·h时,二氧化碳排放量从____
___增加到_____________。
议一议:
(3)小明家本月用电大约110
KW·h、天然气20m3、自来水5t、油耗75L,请你计算一下小明家这几
项的二氧化碳排放量。
1、在地球某地,温度T(℃)与高度d(m)的关系可以
近似地用
来表示,
根据这个关系式,当d的值分别是200,400,600,800,1000时,计算相应的T值,并用表格表示所得结果。
2.如图所示,长方形的长为12,宽为x,则:
①设长方形面积S,写出S与x的关系式。
②若用C表示长方形的周长,写出周长C与宽x之间的关系式。
说说,你有哪些
收获和困惑?
畅所欲言
谢谢聆听!
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
