人教A版高中数学必修三第二章2.3.2 两个变量的线性相关教学 课件 (共21张PPT)
文档属性
| 名称 | 人教A版高中数学必修三第二章2.3.2 两个变量的线性相关教学 课件 (共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-05 09:51:02 | ||
图片预览







文档简介
(共21张PPT)
2.3.2
两个变量的线性相关
普通高中课程标准实验教科书人教A版《数学》(必修3)第二章《统计》第3节
函数关系
匀速直线运动中
的路程s和时间t
相关关系
体重y和身高x
探究:银川一中在校学生的体重
y(kg)和身高x(cm)之间的关系。
分组探究过程
收集数据和选择样本
那么,经过以上展示、分析,我们在探究“银川一中在校学生的体重和身高之间的关系”时,应该怎样选取样本呢?
第一:样本容量为?
第二:用哪种随机抽样方法?
第三:收集完数据之后可如何处理数据?
请依据散点图,预测一下学校身高为188cm的同学的体重?
提出问题
线性相关关系、回归直线
回归方程
如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线叫做回归直线。
回归直线的方程简称回归方程。
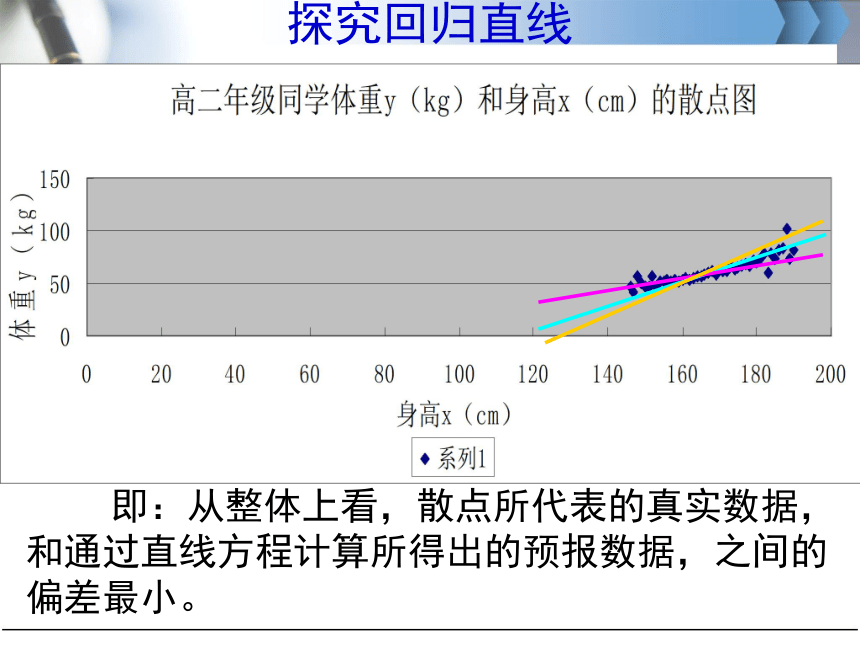
探究回归直线
即:从整体上看,散点所代表的真实数据,和通过直线方程计算所得出的预报数据,之间的偏差最小。
纵
向
距
离
探究回归方程
偏差之和为:
最小二乘法
这种通过求(1)式的最小值而得到回归方程的方法,即使得样本数据的点到回归直线的距离的平方和最小的方法叫做最小二乘法。
回归直线必过点
借助计算机Excel软件,迅速能得到身高和体重这两个变量的回归直线和回归方程。
确定回归方程
理解回归方程的预报作用
计算x=175cm时,y的预报值,对比真实值和预报值。
解决问题
利用回归方程,预测学校身高为188cm的同学的体重?
在现实问题的分析中,为了使得统计推断更具可信度,我们常常需要考虑随机误差,即建立线性回归模型
其中
表示随机误差来分析线性相关关系。
下面,我们一起来对比,用已知的回归方程预测下列不同个体的体重时,哪个可信度更高。
1、1999年银川一中某个188cm的同学的体重;银川一中现在在校某个188cm的同学的体重。
2、重庆某个188cm的人的体重;银川一中现在在校某个188cm的同学的体重。
回归方程做统计推断时的局限性
回归直线方程有时效性
回归直线方程只适用于所研究的样本的总体
回归方程做统计推断时的局限性
以上,我们经历了对具有线性相关关系的两个变量进行统计分析的完整的过程,我们称为回归分析。回顾整个过程,谁来归纳小结一下:对具有线性相关关系的两个变量进行回归分析的具体流程?
归纳回归分析的流程
收集数据
画散点图
确定回归直线方程
做出统计推断
这节课我们掌握了用回归分析的方法来研究具有线性相关关系的两个变量,课后,请大家选择自己感兴趣的实际问题,进行研究,形成研究报告,并互相交流。
2.3.2
两个变量的线性相关
普通高中课程标准实验教科书人教A版《数学》(必修3)第二章《统计》第3节
函数关系
匀速直线运动中
的路程s和时间t
相关关系
体重y和身高x
探究:银川一中在校学生的体重
y(kg)和身高x(cm)之间的关系。
分组探究过程
收集数据和选择样本
那么,经过以上展示、分析,我们在探究“银川一中在校学生的体重和身高之间的关系”时,应该怎样选取样本呢?
第一:样本容量为?
第二:用哪种随机抽样方法?
第三:收集完数据之后可如何处理数据?
请依据散点图,预测一下学校身高为188cm的同学的体重?
提出问题
线性相关关系、回归直线
回归方程
如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线叫做回归直线。
回归直线的方程简称回归方程。
探究回归直线
即:从整体上看,散点所代表的真实数据,和通过直线方程计算所得出的预报数据,之间的偏差最小。
纵
向
距
离
探究回归方程
偏差之和为:
最小二乘法
这种通过求(1)式的最小值而得到回归方程的方法,即使得样本数据的点到回归直线的距离的平方和最小的方法叫做最小二乘法。
回归直线必过点
借助计算机Excel软件,迅速能得到身高和体重这两个变量的回归直线和回归方程。
确定回归方程
理解回归方程的预报作用
计算x=175cm时,y的预报值,对比真实值和预报值。
解决问题
利用回归方程,预测学校身高为188cm的同学的体重?
在现实问题的分析中,为了使得统计推断更具可信度,我们常常需要考虑随机误差,即建立线性回归模型
其中
表示随机误差来分析线性相关关系。
下面,我们一起来对比,用已知的回归方程预测下列不同个体的体重时,哪个可信度更高。
1、1999年银川一中某个188cm的同学的体重;银川一中现在在校某个188cm的同学的体重。
2、重庆某个188cm的人的体重;银川一中现在在校某个188cm的同学的体重。
回归方程做统计推断时的局限性
回归直线方程有时效性
回归直线方程只适用于所研究的样本的总体
回归方程做统计推断时的局限性
以上,我们经历了对具有线性相关关系的两个变量进行统计分析的完整的过程,我们称为回归分析。回顾整个过程,谁来归纳小结一下:对具有线性相关关系的两个变量进行回归分析的具体流程?
归纳回归分析的流程
收集数据
画散点图
确定回归直线方程
做出统计推断
这节课我们掌握了用回归分析的方法来研究具有线性相关关系的两个变量,课后,请大家选择自己感兴趣的实际问题,进行研究,形成研究报告,并互相交流。
