人教版数学必修4第一章1.1.2 弧度制 课件(共21张PPT)
文档属性
| 名称 | 人教版数学必修4第一章1.1.2 弧度制 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-06 15:46:59 | ||
图片预览







文档简介
(共21张PPT)
人教版A版数学必修4
一、创设情境,导入新知
1公里=1000米
孙杨在里约奥运会获得200米自由泳金牌!
0.2公里自由泳!
一、创设情境,导入新知
——弧度制
角度制:将一个周角均分成360份,每一份代表1度。
(单位:度、分、秒)
故圆周角等于360°,平角等于180°,直角等于90°
快问快答:
1°13'+1°47'=?
1°7'+1°8'=?
2°60′=3°
2°15'
60进制
11+29=?
40
分小组合作:
二、动手感知,建构概念
第一小组
陈焕焕
陈奕州
陈小慧
王芳琴
王素筝
二
罗海振
谢楷林
王士鹏
吴宗尧
沈家昭
三
符林颖
林家能
黄莹
梁燕英
欧成敏
四
黄星晓
陈燕妮
陈伟小
林送转
陈倩汝
五
孙昌淋
符凤玉
陈子梦
王章乔
陈丽莹
六
周智群
林小玉
陈红艳
李婷婷
陈佳斯
七
符婷婷
刘佳恩
羊少果
陈樱娇
符佳佳
八
邓小科
王波
王学强
吴燕归
王燕丽
九
苏丽萍
钟小娴
谢澈
谢国锃
王萌玉
十
庞宛阁
陈流瑾
许康柔
倪敏泽
秦瑞晖
十一
王梦真
王佳逾
方媛
吴长青
王永志
二、动手感知,建构概念
实验1:
(1)阅读教材中对1弧度角的概念的描述;
(2)如何在圆形卡纸上作出1弧度角?
(3)以小组为单位,相互交流1弧度角的画法。
实验准备:每人准备一大一小的两张圆形卡纸、一根无弹性的绳子。
二、动手感知,建构概念
定义:把长度等于半径长的弧所对的圆心角叫做1弧度角。
注:单位用rad表示,读作弧度。
单位通常可以省略不写。
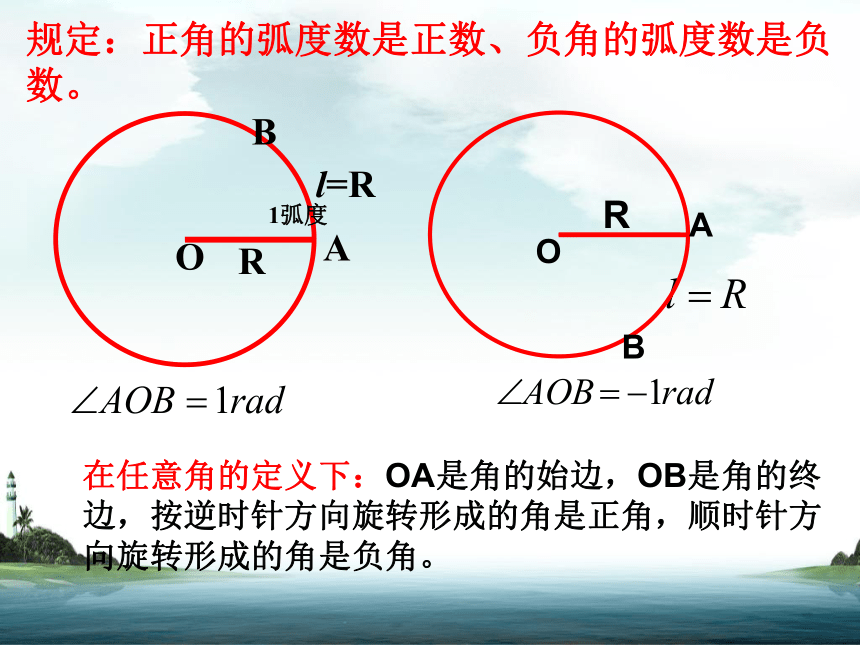
在任意角的定义下:OA是角的始边,OB是角的终边,按逆时针方向旋转形成的角是正角,顺时针方向旋转形成的角是负角。
O
A
B
规定:正角的弧度数是正数、负角的弧度数是负数。
R
三、合作交流,探究性质
实验2:
(1)请在大小两张圆形卡纸上分别作出
1弧度角;
(2)观察、比较所作出两个1弧度角的大小;
(3)小组合作交流,说一说你的发现。
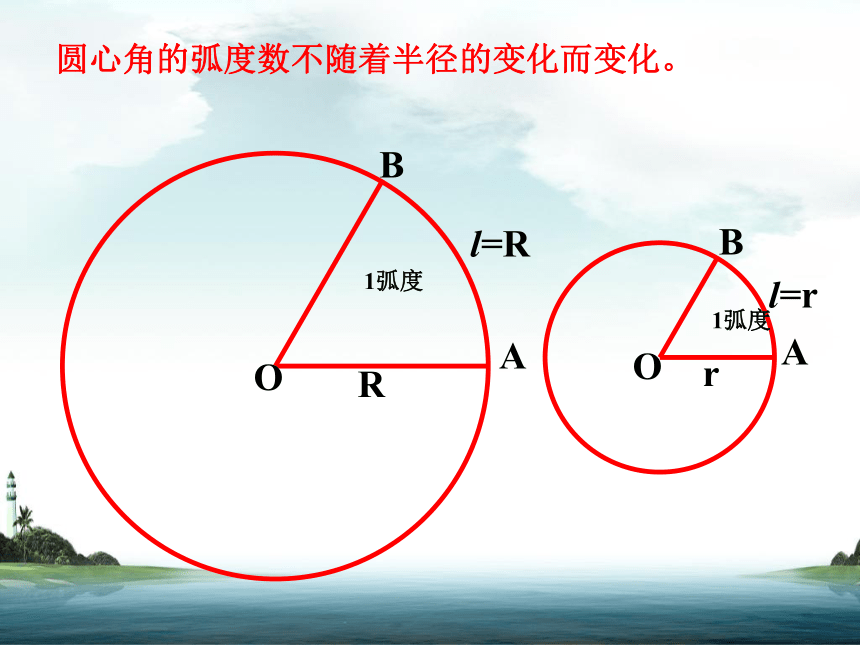
圆心角的弧度数不随着半径的变化而变化。
思考:如果弧长是
,半径是r,那么弧所对的圆心角
的弧度数是多少?
探究:如图,半径为r的圆的圆心与原点重合,角的终边与x轴的正半轴重合,交圆于点A,终边与圆交于点B.
请完成表格.
三、合作交流,探究性质
⌒
1
2r
3
2r
逆时针
顺时针
圆心角
的正负是由
的终边的旋转方向决定,圆心角的弧度数的绝对值等于弧长和半径的比值。
弧长AB
r
3r
半径r
r
r
r
r
圆心角
2
-2
OB旋转方向
逆时针
逆时针
弧长
、半径r、圆心角
三者之间的关系
已知圆的半径为r
(1)计算圆的周长=______,由此得出圆周角的弧度数=_____
;
(2)圆周角的度数=_____;
(3)得出结论:
=______(填弧度数)
即
=______(填弧度数);
(4)1弧度=_______≈_____(填角度数)
(5)1°=_______≈________(填弧度数).
2πr
2π
360°
2π
π
57.3°
角度制和弧度制的换算:
1、本节课你学习了什么内容?
2、在本节课中你对哪部分内容记忆最深刻,可谈谈你的感受。
3、你还有什么困惑吗?
五、归纳小结,发展与深化
弧度制
定义:把长度等于半径长的弧所对的圆心角叫做1弧度角。
规定:任意角定义下,正角的弧度数是正数
,负角的弧度数是负数,零角是0.
角度制和弧度制的换算:
弧度制和角度制有什么区别和联系呢?
五、归纳小结,发展与深化
1、两种单位都是度量角的大小的单位制;
2、角度制是六十进制,弧度制是十进制,角的概念推广之后,在弧度制下,角的集合和实数R之间建立一种一一对应的关系。
3、弧度制将弧长和线段度量统一起来。
一、弧度制的发明——托勒密。
1、托勒密大约于公元90年出生在希腊。
2、托勒密真正创立了天文学,并且计算出诸多天体运行轨迹的是两千年前古罗马时代的托勒密。
3、托勒密发明了球坐标,定义了包括赤道和零度经线在内的经纬线,他提出了黄道,还发明了弧度制。
五、归纳小结,发展与深化
二、弧度制思想的提出——欧拉
1、18世纪以前,人们一直是用线段的长来定义三角函数的.
2、直至1748年,瑞士数学家欧拉
在出版的一部划时代的著作《无穷小分析概论》中,提出了弧度制的思想.这一思想将线段与弧的度量单位统一起来,大大简化了某些三角公式及计算.
五、归纳小结,发展与深化
三、弧度制的正式提出——汤姆生
1873年6月5日,数学教师汤姆生首先使用了“弧度”一词.当时,他将“半径”(radius)的前四个字母与“角”(angle)的前两个字母合在一起,构成radian。
并被人们广泛接受和引用.我国学者曾把radian译成“弪’(由“弧”与“径”两字的一部分拼成).中华人民共和国成立以来,中学数学教科书中都把radian译作“弧度”.
五、归纳小结,发展与深化
任何一个数学知识点都经历上百年甚至上千年的探索。
孙杨夺冠背后有着无数努力的汗水!
学习同样不是一件一蹴而就的事情,是量变到质变的过程!
人教版A版数学必修4
一、创设情境,导入新知
1公里=1000米
孙杨在里约奥运会获得200米自由泳金牌!
0.2公里自由泳!
一、创设情境,导入新知
——弧度制
角度制:将一个周角均分成360份,每一份代表1度。
(单位:度、分、秒)
故圆周角等于360°,平角等于180°,直角等于90°
快问快答:
1°13'+1°47'=?
1°7'+1°8'=?
2°60′=3°
2°15'
60进制
11+29=?
40
分小组合作:
二、动手感知,建构概念
第一小组
陈焕焕
陈奕州
陈小慧
王芳琴
王素筝
二
罗海振
谢楷林
王士鹏
吴宗尧
沈家昭
三
符林颖
林家能
黄莹
梁燕英
欧成敏
四
黄星晓
陈燕妮
陈伟小
林送转
陈倩汝
五
孙昌淋
符凤玉
陈子梦
王章乔
陈丽莹
六
周智群
林小玉
陈红艳
李婷婷
陈佳斯
七
符婷婷
刘佳恩
羊少果
陈樱娇
符佳佳
八
邓小科
王波
王学强
吴燕归
王燕丽
九
苏丽萍
钟小娴
谢澈
谢国锃
王萌玉
十
庞宛阁
陈流瑾
许康柔
倪敏泽
秦瑞晖
十一
王梦真
王佳逾
方媛
吴长青
王永志
二、动手感知,建构概念
实验1:
(1)阅读教材中对1弧度角的概念的描述;
(2)如何在圆形卡纸上作出1弧度角?
(3)以小组为单位,相互交流1弧度角的画法。
实验准备:每人准备一大一小的两张圆形卡纸、一根无弹性的绳子。
二、动手感知,建构概念
定义:把长度等于半径长的弧所对的圆心角叫做1弧度角。
注:单位用rad表示,读作弧度。
单位通常可以省略不写。
在任意角的定义下:OA是角的始边,OB是角的终边,按逆时针方向旋转形成的角是正角,顺时针方向旋转形成的角是负角。
O
A
B
规定:正角的弧度数是正数、负角的弧度数是负数。
R
三、合作交流,探究性质
实验2:
(1)请在大小两张圆形卡纸上分别作出
1弧度角;
(2)观察、比较所作出两个1弧度角的大小;
(3)小组合作交流,说一说你的发现。
圆心角的弧度数不随着半径的变化而变化。
思考:如果弧长是
,半径是r,那么弧所对的圆心角
的弧度数是多少?
探究:如图,半径为r的圆的圆心与原点重合,角的终边与x轴的正半轴重合,交圆于点A,终边与圆交于点B.
请完成表格.
三、合作交流,探究性质
⌒
1
2r
3
2r
逆时针
顺时针
圆心角
的正负是由
的终边的旋转方向决定,圆心角的弧度数的绝对值等于弧长和半径的比值。
弧长AB
r
3r
半径r
r
r
r
r
圆心角
2
-2
OB旋转方向
逆时针
逆时针
弧长
、半径r、圆心角
三者之间的关系
已知圆的半径为r
(1)计算圆的周长=______,由此得出圆周角的弧度数=_____
;
(2)圆周角的度数=_____;
(3)得出结论:
=______(填弧度数)
即
=______(填弧度数);
(4)1弧度=_______≈_____(填角度数)
(5)1°=_______≈________(填弧度数).
2πr
2π
360°
2π
π
57.3°
角度制和弧度制的换算:
1、本节课你学习了什么内容?
2、在本节课中你对哪部分内容记忆最深刻,可谈谈你的感受。
3、你还有什么困惑吗?
五、归纳小结,发展与深化
弧度制
定义:把长度等于半径长的弧所对的圆心角叫做1弧度角。
规定:任意角定义下,正角的弧度数是正数
,负角的弧度数是负数,零角是0.
角度制和弧度制的换算:
弧度制和角度制有什么区别和联系呢?
五、归纳小结,发展与深化
1、两种单位都是度量角的大小的单位制;
2、角度制是六十进制,弧度制是十进制,角的概念推广之后,在弧度制下,角的集合和实数R之间建立一种一一对应的关系。
3、弧度制将弧长和线段度量统一起来。
一、弧度制的发明——托勒密。
1、托勒密大约于公元90年出生在希腊。
2、托勒密真正创立了天文学,并且计算出诸多天体运行轨迹的是两千年前古罗马时代的托勒密。
3、托勒密发明了球坐标,定义了包括赤道和零度经线在内的经纬线,他提出了黄道,还发明了弧度制。
五、归纳小结,发展与深化
二、弧度制思想的提出——欧拉
1、18世纪以前,人们一直是用线段的长来定义三角函数的.
2、直至1748年,瑞士数学家欧拉
在出版的一部划时代的著作《无穷小分析概论》中,提出了弧度制的思想.这一思想将线段与弧的度量单位统一起来,大大简化了某些三角公式及计算.
五、归纳小结,发展与深化
三、弧度制的正式提出——汤姆生
1873年6月5日,数学教师汤姆生首先使用了“弧度”一词.当时,他将“半径”(radius)的前四个字母与“角”(angle)的前两个字母合在一起,构成radian。
并被人们广泛接受和引用.我国学者曾把radian译成“弪’(由“弧”与“径”两字的一部分拼成).中华人民共和国成立以来,中学数学教科书中都把radian译作“弧度”.
五、归纳小结,发展与深化
任何一个数学知识点都经历上百年甚至上千年的探索。
孙杨夺冠背后有着无数努力的汗水!
学习同样不是一件一蹴而就的事情,是量变到质变的过程!
