人教版数学必修4第一章1.1.2弧度制课件(共20张PPT)
文档属性
| 名称 | 人教版数学必修4第一章1.1.2弧度制课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-06 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
1.1.2
弧度制
引入新课
1.我们学习了角的概念的推广知道角可以分为哪几类?
“正角”与“负角”“0角”
2.要描述一个角的大小,通常用什么表示呢?
是用度来表示的
4.在半径为r的圆中,n°的圆心角所对的圆弧长如何计算?
3.那么1°的角是如何定义的?
1°的角可以理解为将圆周角分成360等份,
每一等份的弧所对的圆心角就是它是一个定值,
与所取圆的半径大小无关.
引入新课
5.
圆心角的大小是否与圆半径的大小有关?
探究新知
(一)弧度制的概念
讨论:角除了以度为单位,还有分和秒,他们是六十进制的,计算不方便,角的度量是否也能用不同的单位制?(类比长度的度量单位)
新知1:弧度制的定义
规定长度等于半径长的圆弧
所对的圆心角叫做1弧度的角.
以弧度为单位来度量角的
制度叫做弧度制.
在弧度制下,1弧度记作1
rad.
弧度制定义的三点说明
1.弧度制是以“弧度”为单位来度量角的单位制,
角度制是以“度”为单位来度量角的单位制.
2.
1弧度是等于半径长的弧所对的圆心角(或这条
弧)的大小,而1°的角是周角的1/360
.
3.无论是以“弧度”还是以“度”为单位,
角的大小都是一个与半径大小无关的定值.
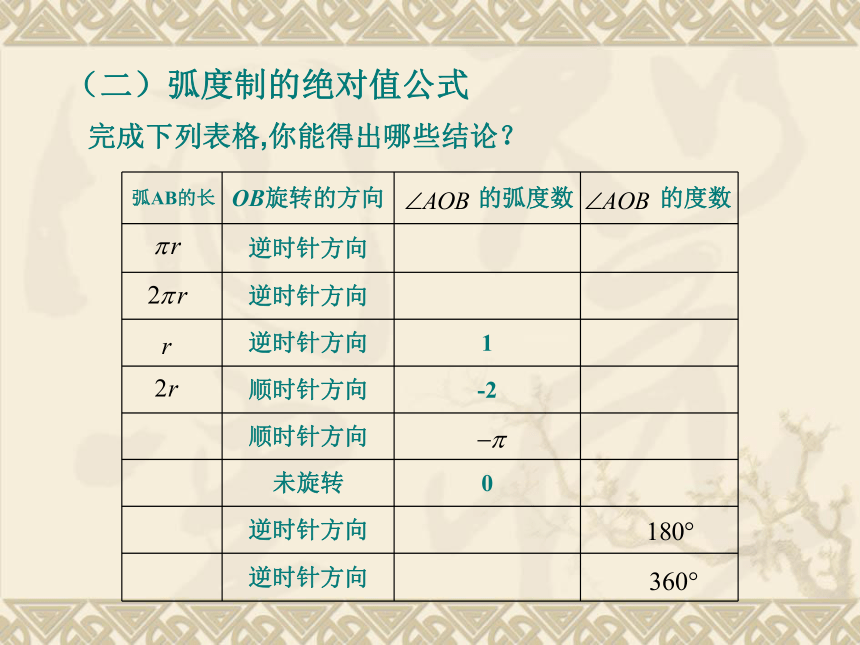
(二)弧度制的绝对值公式
完成下列表格,你能得出哪些结论?
弧AB的长
OB旋转的方向
的弧度数
的度数
逆时针方向
逆时针方向
逆时针方向
1
顺时针方向
-2
顺时针方向
未旋转
0
逆时针方向
逆时针方向
的长
OB旋转的方向
的弧度数
的度数
逆时针方向
逆时针方向
逆时针方向
1
顺时针方向
-2
顺时针方向
0
未旋转
0
逆时针方向
逆时针方向
(1)一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0.
新知2:
(三)弧度与角度的换算
360°=2π
rad
180°=π
rad
理解新知
1.关键是弄清1弧度的角的概念:长度等于半径长
的圆弧所对的圆心角叫做1弧度的角.
2.无论是以“弧度”还是以“度”为单位,角的大
小都是一个与半径大小无关的定值.
3.正角的弧度数是一个正数,负角的弧度数是一
个负数,零角的弧度数是0.
5.角度制与弧度制换算
:180°=π
rad
运用新知
例1按照下列要求,把67°30′化成弧度:
(1)精确值;
(2)精确到0.001的近似值.
(2)利用计算器计算
运用新知
解:
特别说明:
例1和例2都是角度和弧度的换算,
要注意度的单位和弧度的单位一定不能省略.
根据度与弧度的换算关系,下表中各特殊角对应的弧度数分别是多少?
运用新知
注意:用弧度制表示角时,“弧度”二字或“rad”通常略去不写,而只写该角所对应的弧度数.如α=2表示α是2rad的角.
随堂练习:
例3.利用弧度制证明下列关于扇形的公式:
运用新知
课堂小结
课堂小结
布置作业
1.1.2
弧度制
引入新课
1.我们学习了角的概念的推广知道角可以分为哪几类?
“正角”与“负角”“0角”
2.要描述一个角的大小,通常用什么表示呢?
是用度来表示的
4.在半径为r的圆中,n°的圆心角所对的圆弧长如何计算?
3.那么1°的角是如何定义的?
1°的角可以理解为将圆周角分成360等份,
每一等份的弧所对的圆心角就是它是一个定值,
与所取圆的半径大小无关.
引入新课
5.
圆心角的大小是否与圆半径的大小有关?
探究新知
(一)弧度制的概念
讨论:角除了以度为单位,还有分和秒,他们是六十进制的,计算不方便,角的度量是否也能用不同的单位制?(类比长度的度量单位)
新知1:弧度制的定义
规定长度等于半径长的圆弧
所对的圆心角叫做1弧度的角.
以弧度为单位来度量角的
制度叫做弧度制.
在弧度制下,1弧度记作1
rad.
弧度制定义的三点说明
1.弧度制是以“弧度”为单位来度量角的单位制,
角度制是以“度”为单位来度量角的单位制.
2.
1弧度是等于半径长的弧所对的圆心角(或这条
弧)的大小,而1°的角是周角的1/360
.
3.无论是以“弧度”还是以“度”为单位,
角的大小都是一个与半径大小无关的定值.
(二)弧度制的绝对值公式
完成下列表格,你能得出哪些结论?
弧AB的长
OB旋转的方向
的弧度数
的度数
逆时针方向
逆时针方向
逆时针方向
1
顺时针方向
-2
顺时针方向
未旋转
0
逆时针方向
逆时针方向
的长
OB旋转的方向
的弧度数
的度数
逆时针方向
逆时针方向
逆时针方向
1
顺时针方向
-2
顺时针方向
0
未旋转
0
逆时针方向
逆时针方向
(1)一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0.
新知2:
(三)弧度与角度的换算
360°=2π
rad
180°=π
rad
理解新知
1.关键是弄清1弧度的角的概念:长度等于半径长
的圆弧所对的圆心角叫做1弧度的角.
2.无论是以“弧度”还是以“度”为单位,角的大
小都是一个与半径大小无关的定值.
3.正角的弧度数是一个正数,负角的弧度数是一
个负数,零角的弧度数是0.
5.角度制与弧度制换算
:180°=π
rad
运用新知
例1按照下列要求,把67°30′化成弧度:
(1)精确值;
(2)精确到0.001的近似值.
(2)利用计算器计算
运用新知
解:
特别说明:
例1和例2都是角度和弧度的换算,
要注意度的单位和弧度的单位一定不能省略.
根据度与弧度的换算关系,下表中各特殊角对应的弧度数分别是多少?
运用新知
注意:用弧度制表示角时,“弧度”二字或“rad”通常略去不写,而只写该角所对应的弧度数.如α=2表示α是2rad的角.
随堂练习:
例3.利用弧度制证明下列关于扇形的公式:
运用新知
课堂小结
课堂小结
布置作业
