人教版数学必修4第一章1.2.1任意角的三角函数课件(共21张PPT)
文档属性
| 名称 | 人教版数学必修4第一章1.2.1任意角的三角函数课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-06 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
P
y
x
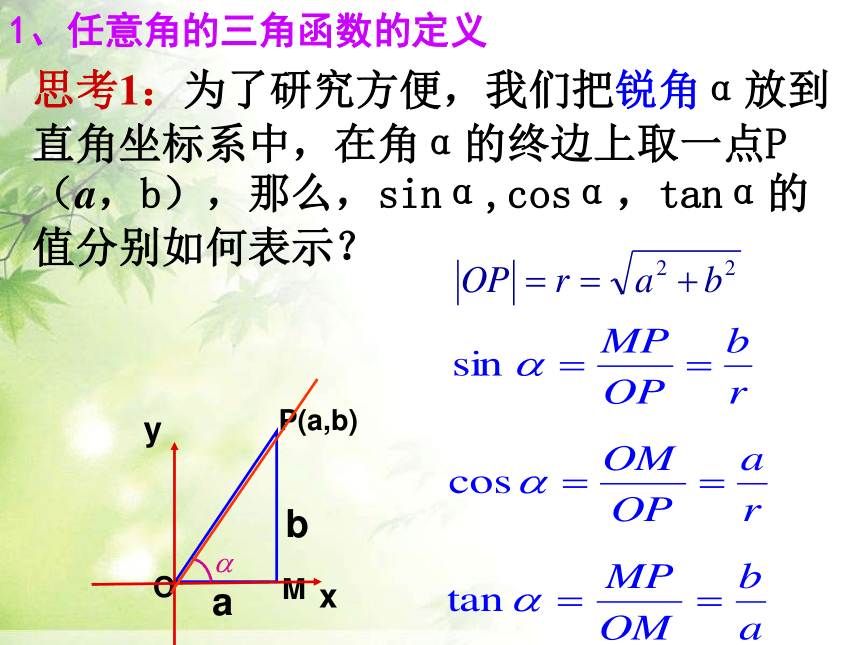
思考1:为了研究方便,我们把锐角α放到直角坐标系中,在角α的终边上取一点P(a,b),那么,sinα,cosα,tanα的值分别如何表示?
1、任意角的三角函数的定义
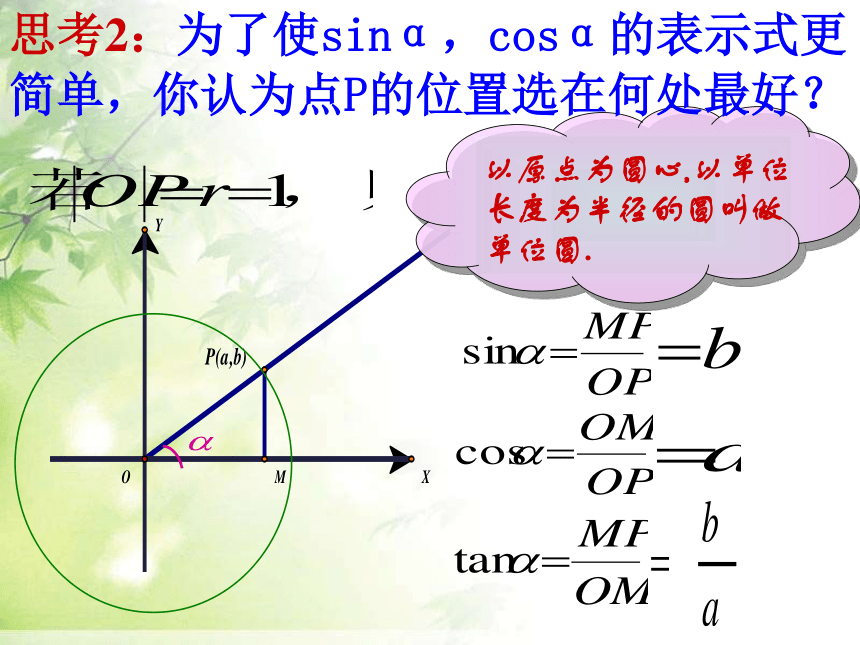
思考2:为了使sinα,cosα的表示式更简单,你认为点P的位置选在何处最好?
α的终边
P(x,y)
O
x
y
P(x,y)
α的终边
思考3:设α是一个任意角,它的终边与单位圆交于点P(x,y),为了与当α为锐角时的三角函数保持统一,你认为sinα,cosα,tanα对应的值应分别如何定义?
对应关系
,
,
都是以角为自变量,以单位圆
上的点的坐标或坐标的比值为函数值的函数,
分别称为正弦函数、余弦函数和正切函数,
并统称为三角函数.
思考4:三角函数该如何定义呢?
例1、求
的正弦,余弦,正切的值
O
点评:若已知角α的大小,可求出角α终边与单位圆的交点,然后再利用定义求三角函数值。
∵
∴
正切函数的定义域是
正、余弦函数的定义域为R,
思考5:在弧度制中,这三个三角函数的
定义域分别是什么?
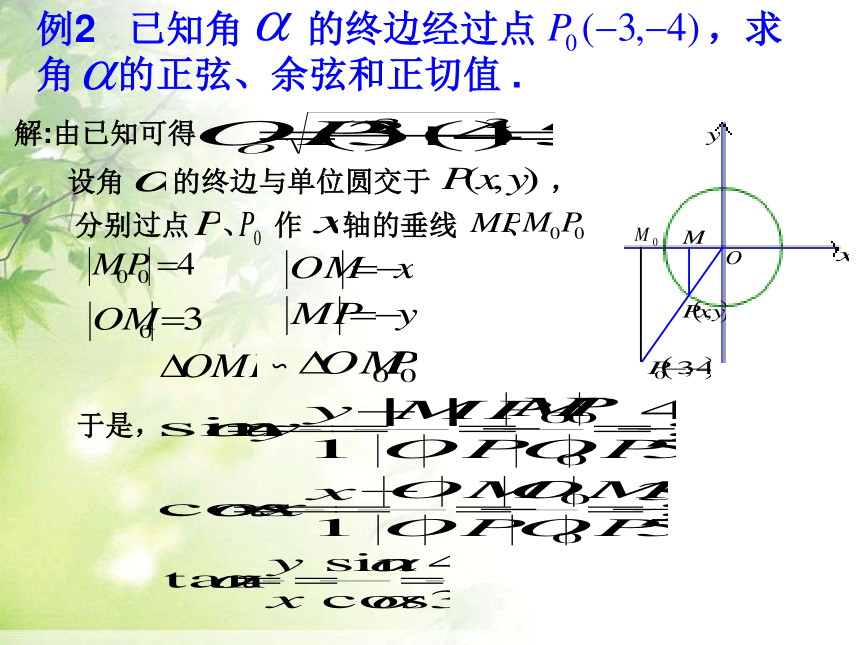
例2
已知角
的终边经过点
,求角
的正弦、余弦和正切值
.
\
于是,
定义推广:
于是,
解:由已知可得:
全为+
一全正
二正弦
三正切
四余弦
规律:
2、三角函数值的符号
例3、求证:当
成立
时,角θ为第三象限角,反之也成立。
例题讲解
证明:若sinθ<0,那么θ角的终边可能位于第三
或第四象限,也可能位于y轴的非正半轴上
又若tanθ>0,那么θ角的终边可能位于第一或第三象限.
因为①②都成立,所以θ角的终边只能位于第三象限.于是θ为第三象限角。反之,若θ为第三象限角,则①②都成立
练习:确定下列三角函数值的符号:
3、诱导公式(一)
结论:终边相同的角的同一三角函数的值相等.
解:
例4:求下列三角函数值:
1.
内容总结:
(1)任意角三角函数的概念以及它推广的定义。
诱导公式
归纳总结
1.
内容总结:
(2)任意角三角
函数的符号规律。
(3)诱导公式
2、数形结合思想,分类讨论思想
归纳总结
作业:
课本第15页
练习
2、3
课本第20页
习题1.2
A组
2
练习1
特殊角的三角函数:
不存在
不存在
P
y
x
思考1:为了研究方便,我们把锐角α放到直角坐标系中,在角α的终边上取一点P(a,b),那么,sinα,cosα,tanα的值分别如何表示?
1、任意角的三角函数的定义
思考2:为了使sinα,cosα的表示式更简单,你认为点P的位置选在何处最好?
α的终边
P(x,y)
O
x
y
P(x,y)
α的终边
思考3:设α是一个任意角,它的终边与单位圆交于点P(x,y),为了与当α为锐角时的三角函数保持统一,你认为sinα,cosα,tanα对应的值应分别如何定义?
对应关系
,
,
都是以角为自变量,以单位圆
上的点的坐标或坐标的比值为函数值的函数,
分别称为正弦函数、余弦函数和正切函数,
并统称为三角函数.
思考4:三角函数该如何定义呢?
例1、求
的正弦,余弦,正切的值
O
点评:若已知角α的大小,可求出角α终边与单位圆的交点,然后再利用定义求三角函数值。
∵
∴
正切函数的定义域是
正、余弦函数的定义域为R,
思考5:在弧度制中,这三个三角函数的
定义域分别是什么?
例2
已知角
的终边经过点
,求角
的正弦、余弦和正切值
.
\
于是,
定义推广:
于是,
解:由已知可得:
全为+
一全正
二正弦
三正切
四余弦
规律:
2、三角函数值的符号
例3、求证:当
成立
时,角θ为第三象限角,反之也成立。
例题讲解
证明:若sinθ<0,那么θ角的终边可能位于第三
或第四象限,也可能位于y轴的非正半轴上
又若tanθ>0,那么θ角的终边可能位于第一或第三象限.
因为①②都成立,所以θ角的终边只能位于第三象限.于是θ为第三象限角。反之,若θ为第三象限角,则①②都成立
练习:确定下列三角函数值的符号:
3、诱导公式(一)
结论:终边相同的角的同一三角函数的值相等.
解:
例4:求下列三角函数值:
1.
内容总结:
(1)任意角三角函数的概念以及它推广的定义。
诱导公式
归纳总结
1.
内容总结:
(2)任意角三角
函数的符号规律。
(3)诱导公式
2、数形结合思想,分类讨论思想
归纳总结
作业:
课本第15页
练习
2、3
课本第20页
习题1.2
A组
2
练习1
特殊角的三角函数:
不存在
不存在
