人教版数学必修四1.2.2《同角三角函数基本关系》授课课件(共24张PPT)
文档属性
| 名称 | 人教版数学必修四1.2.2《同角三角函数基本关系》授课课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 576.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-06 20:30:25 | ||
图片预览








文档简介
(共24张PPT)
一、创境设问:填一填
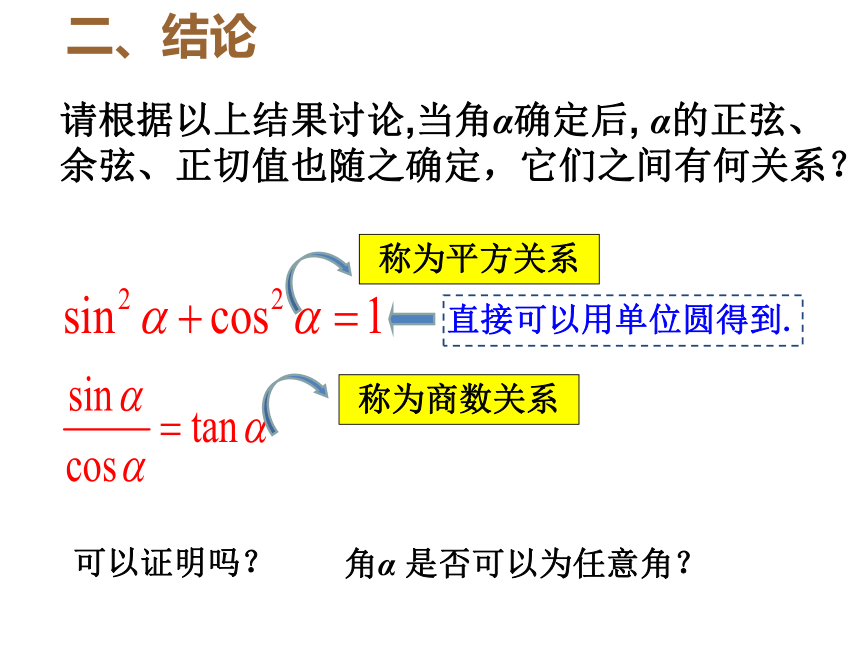
直接可以用单位圆得到.
请根据以上结果讨论,当角α确定后,
α的正弦、余弦、正切值也随之确定,它们之间有何关系?
可以证明吗?
角α
是否可以为任意角?
称为平方关系
二、结论
称为商数关系
Company
Logo
回顾:任意角的三角函数定义
.
一般在直角坐标系中,给定单位圆,对任意的角α,使α的顶点与原点重合,始边与x轴的非负半轴重合,终边与单位圆交于点p(a,b),则点p的纵坐标b叫角α的正弦函数,记作b=sin
α,p的横坐标a叫角α的余弦函数,记作b=cos
α。通常习惯于用x表示自变量,即用x表示角的大小,用y表示函数值,这样就定义了任意角的三角函数y=sinx和y=cosx,它们的定义域为全体实数,值域为【-1,1】.
根据函数定义,比值
是角α的函数,
我们把它叫作角α的正切函数,记作y=tanα,其中α∈R,α≠
+kπ,k∈Z.
y=tanx
判一判
判断下列式子是否成立?
三、数学应用:求值
先定象限,后定值
小结:(1)注意方程思想的运用;
(2)分类讨论的数学思想.
三、数学应用:求值
先定象限,后定值
三、数学应用:求值
例3、已知tan
α=2,求:
化弦为切
化弦为切
妙用“1”,然后再化弦为切
拓展延伸
三、数学应用:求值
例4、已知0<α<π,sinα+cosα=
.
求:(1)sinαcosα;
(2)
sinα-cosα.
三、数学应用:求值
问题4:在利用公式求值中应该注意哪些方面?
符号判定准确;
恰当表述;
步骤清楚。
三、数学应用:求值
例5.化简
三、数学应用:化简
三、数学应用:化简
三、数学应用:化简(练习)
三、数学应用:证明
三、数学应用:证明
分析:由左往右证
例6
求证:
恒等式证明常用方法?
求证:
分析:
三、数学应用:证明
分析:1.两面夹
2.切化弦
三、数学应用:证明
(一)同角三角函数的基本关系式:
平方关系:
商数关系:
(二)公式的应用:
知一求二:由一个角的某一三角函数值
求出其它的两个三角函数值;
(三)数学思想方法:
①分类讨论;
②方程(组)的思想.
小结:
1.证明方法
(1)由左往右证
(2)由右往左证
由复杂的一端向简单的一端化简
(3)两面夹
2.技巧
小结:
欢迎你的提问!
一、创境设问:填一填
直接可以用单位圆得到.
请根据以上结果讨论,当角α确定后,
α的正弦、余弦、正切值也随之确定,它们之间有何关系?
可以证明吗?
角α
是否可以为任意角?
称为平方关系
二、结论
称为商数关系
Company
Logo
回顾:任意角的三角函数定义
.
一般在直角坐标系中,给定单位圆,对任意的角α,使α的顶点与原点重合,始边与x轴的非负半轴重合,终边与单位圆交于点p(a,b),则点p的纵坐标b叫角α的正弦函数,记作b=sin
α,p的横坐标a叫角α的余弦函数,记作b=cos
α。通常习惯于用x表示自变量,即用x表示角的大小,用y表示函数值,这样就定义了任意角的三角函数y=sinx和y=cosx,它们的定义域为全体实数,值域为【-1,1】.
根据函数定义,比值
是角α的函数,
我们把它叫作角α的正切函数,记作y=tanα,其中α∈R,α≠
+kπ,k∈Z.
y=tanx
判一判
判断下列式子是否成立?
三、数学应用:求值
先定象限,后定值
小结:(1)注意方程思想的运用;
(2)分类讨论的数学思想.
三、数学应用:求值
先定象限,后定值
三、数学应用:求值
例3、已知tan
α=2,求:
化弦为切
化弦为切
妙用“1”,然后再化弦为切
拓展延伸
三、数学应用:求值
例4、已知0<α<π,sinα+cosα=
.
求:(1)sinαcosα;
(2)
sinα-cosα.
三、数学应用:求值
问题4:在利用公式求值中应该注意哪些方面?
符号判定准确;
恰当表述;
步骤清楚。
三、数学应用:求值
例5.化简
三、数学应用:化简
三、数学应用:化简
三、数学应用:化简(练习)
三、数学应用:证明
三、数学应用:证明
分析:由左往右证
例6
求证:
恒等式证明常用方法?
求证:
分析:
三、数学应用:证明
分析:1.两面夹
2.切化弦
三、数学应用:证明
(一)同角三角函数的基本关系式:
平方关系:
商数关系:
(二)公式的应用:
知一求二:由一个角的某一三角函数值
求出其它的两个三角函数值;
(三)数学思想方法:
①分类讨论;
②方程(组)的思想.
小结:
1.证明方法
(1)由左往右证
(2)由右往左证
由复杂的一端向简单的一端化简
(3)两面夹
2.技巧
小结:
欢迎你的提问!
