人教版八年级下册数学18.2.3正方形 课件(2课时 共131张)
文档属性
| 名称 | 人教版八年级下册数学18.2.3正方形 课件(2课时 共131张) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-03 00:00:00 | ||
图片预览


文档简介
(共131张PPT)
初二年级
数学
正方形(第一课时)
平行四边形
复习反思,引发思考
一般
特殊
以平行四边形为例,你能说一说如何研究一个几何图形吗?
菱形
矩形
平行四
边形
性
质
定义
边
判定
边
角
对角线
角
对角线
通过平行四边形边、角的特殊化,得到了特殊的平行四边形.
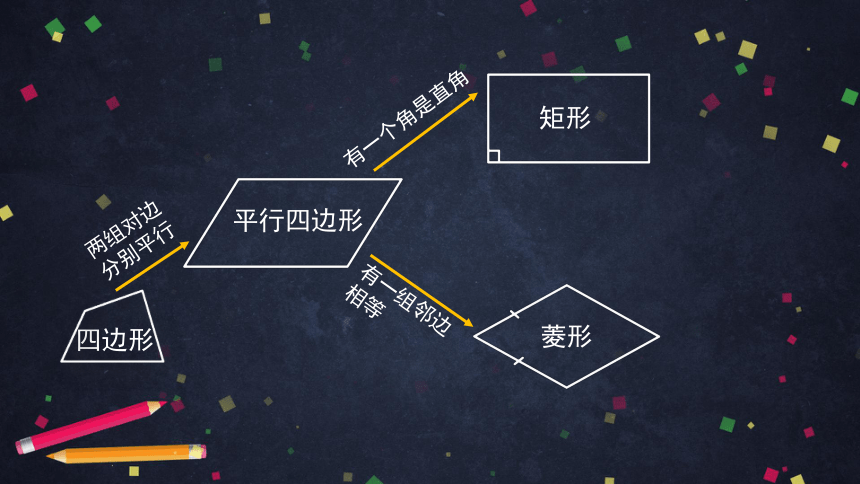
你能说说矩形、菱形与平行四边形有什么关系吗?
有一个角是直角
有一组邻边相等
两组对边
分别平行
四边形
平行四边形
矩形
菱形
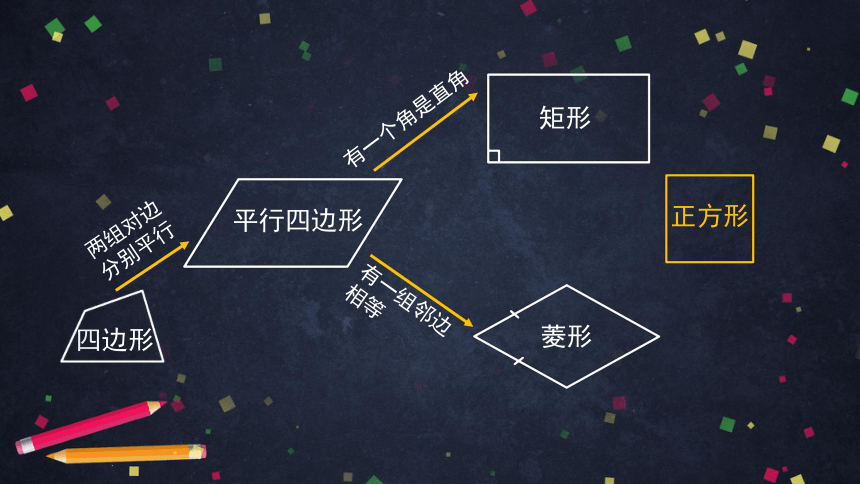
有一个角是直角
两组对边
分别平行
四边形
平行四边形
矩形
菱形
正方形
有一组邻边相等
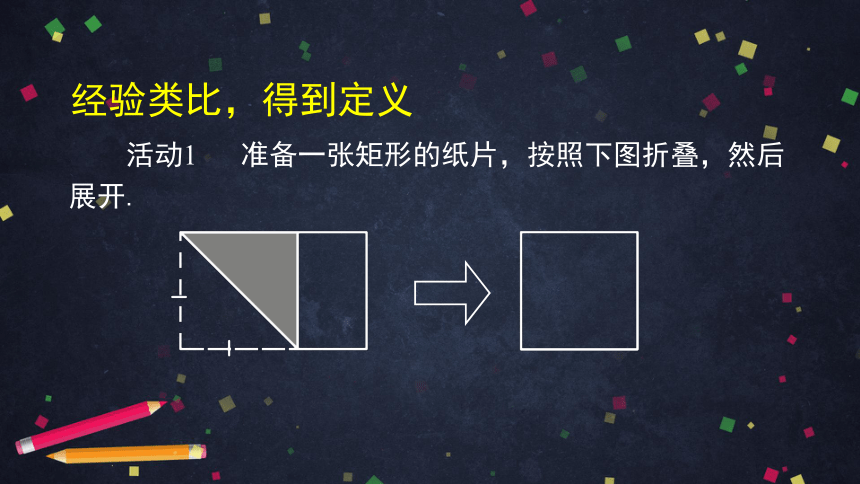
活动1
准备一张矩形的纸片,按照下图折叠,然后展开.
经验类比,得到定义
正方形
经验类比,得到定义
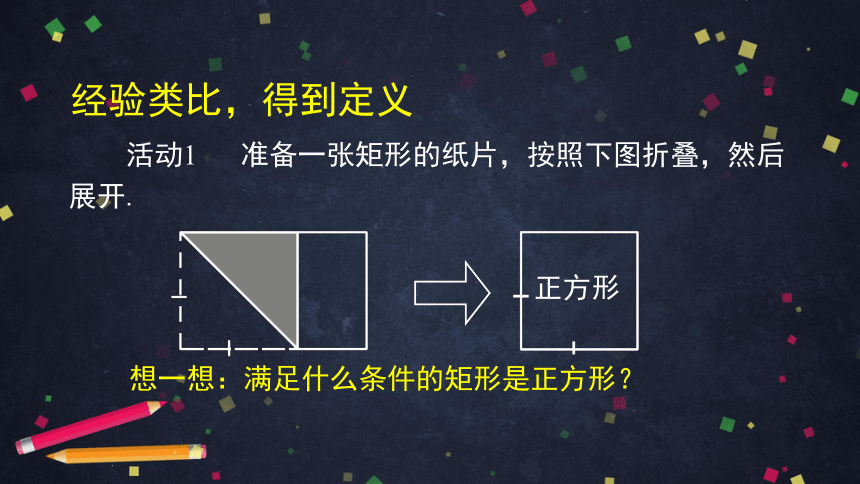
活动1
准备一张矩形的纸片,按照下图折叠,然后展开.
想一想:满足什么条件的矩形是正方形?
经验类比,得到定义
正方形
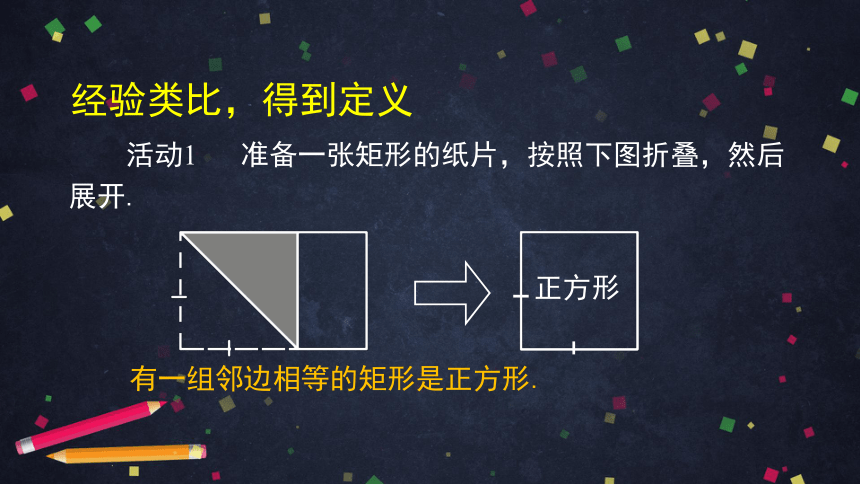
活动1
准备一张矩形的纸片,按照下图折叠,然后展开.
有一组邻边相等的矩形是正方形.
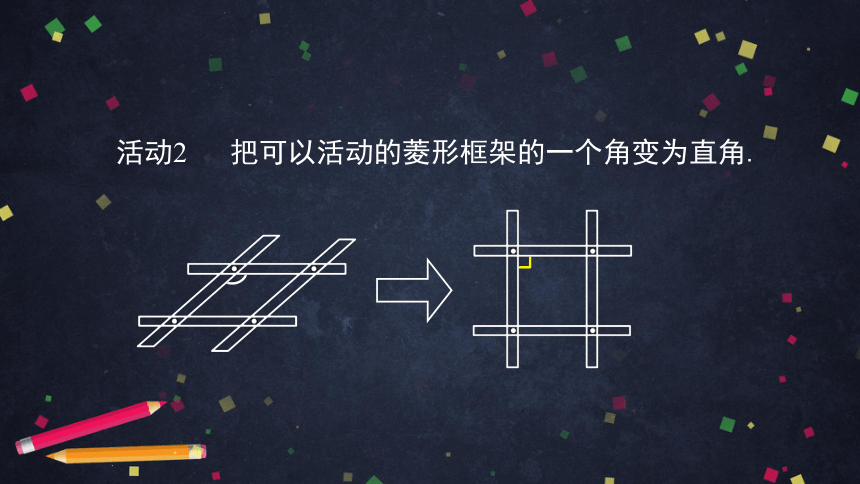
活动2
把可以活动的菱形框架的一个角变为直角.
想一想:满足什么条件的菱形是正方形?
活动2
把可以活动的菱形框架的一个角变为直角.
活动2
把可以活动的菱形框架的一个角变为直角.
有一个角是直角的菱形是正方形.
有一个角是直角
两组对边
分别平行
四边形
平行四边形
矩形
菱形
正方形
有一个角是直角
有一组邻边相等
有一个角是直角
有一组邻边相等
有一组邻边相等
正方形的定义
有一组邻边相等的矩形是正方形.
有一个角是直角的菱形是正方形.
有一个角是直角且有一组邻边相等的平行四边形是正方形.
正方形既是矩形,又是菱形.它具有矩形的性质,
又有菱形的性质.
B
C
A
D
O
你得到了哪些性质?
理性思考,获得定理
边
角
对角线
猜想1
正方形的四条边都相等.
四条边都相等
性质1
正方形的四条边都相等.
A
B
C
D
∵
四边形ABCD是正方形,
∴
AB=BC=CD=DA.
猜想2
正方形的四个角都是直角.
四个角都是直角
性质2
正方形的四个角都是直角.
A
B
C
D
∵
四边形ABCD是正方形,
∴
∠A=∠B=∠C=∠D=90°.
猜想:正方形的对角线相等,并且互相垂直平分.
已知:如图,四边形ABCD是正方形,对角线AC,BD相交于点O.
求证:AC=BD,AC⊥BD,AO=BO=CO=DO.
B
C
A
D
O
正方形
菱形
矩形
AC=BD
AC⊥BD
AO=CO,
BO=DO
AO=BO=CO=DO
证明:∵
正方形ABCD是矩形,
∴
AC=BD.
∵
正方形ABCD是平行四边形,
∴
AO=CO,BO=DO.
∴
AO=BO=CO=DO.
∵
正方形ABCD是菱形,
∴
AC⊥BD.
B
C
A
D
O
性质3
正方形的对角线相等,并且互相垂直平分.
∵
四边形ABCD是正方形,
∴
AC=BD,AC⊥BD,
AO=BO=CO=DO.
B
C
A
D
O
正方形是轴对称图形,它有四条对称轴,分别是对边中点的连线以及两条对角线所在的直线.
正方形是轴对称图形吗?
它的对称轴是什么?
对称性
B
C
A
D
O
正方形
边
角
对角线
矩形
四个角都是直角
对角线相等
菱形
四条边都相等
对角线互相垂直,并且每一条对角线平分一组对角
正方形的四条边都相等.
正方形的四个角都是直角.
正方形的对角线相等,并且互相垂直平分.
正方形的性质
用定义判定:
有一个角是直角且有一组邻边相等的平行四边形是正方形.
有一个角是直角的菱形是正方形.
有一组邻边相等的矩形是正方形.
矩形
菱形
正方形
有一组邻边相等
有一个角是直角
矩形
正方形
边
角
对角线
?
有一组邻边相等
猜想:对角线互相垂直的矩形是正方形.
已知:如图,四边形ABCD是矩形,对角线AC,BD相交于点O,AC⊥BD.
求证:四边形ABCD是正方形.
B
C
A
D
O
B
C
A
D
O
AC⊥BD
OB=OD
四边形ABCD是正方形
四边形ABCD是矩形
AB=AD
B
C
A
D
O
证明:∵
四边形ABCD是矩形,
∴
BO=DO.
∵
AC⊥BD,
∴
AB=AD.
∴
四边形ABCD是正方形.
判定
对角线互相垂直的矩形是正方形.
∵
四边形ABCD是矩形,AC⊥BD,
∴
四边形ABCD是正方形.
B
C
A
D
O
矩形
有一组邻边相等
对角线互相垂直
正方形
猜想:对角线相等的菱形是正方形.
已知:如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=BD.
求证:四边形ABCD是正方形.
B
C
A
D
O
B
C
A
D
O
AC=BD
四边形ABCD是正方形
四边形ABCD是菱形
四个等腰直角三角形
有一个角是直角
AO=CO,BO=DO,AC⊥BD
证明:∵
四边形ABCD是菱形,
∴
AO=CO,BO=DO,AC⊥BD.
∵
AC=BD,
∴
AO=BO=CO=DO.
∴
△AOD,△AOB是等腰直角三角形.
∴
∠BAO=∠DAO=45°.
∴
∠DAB=90°.
∴
四边形ABCD是正方形.
B
C
A
D
O
判定
对角线相等的菱形是正方形.
∵
四边形ABCD是菱形,AC=BD,
∴
四边形ABCD是正方形.
B
C
A
D
O
有一个角是直角
对角线相等
菱形
正方形
正方形的判定
平行四边形
先判定矩形
再判定菱形
先判定菱形
再判定矩形
正方形
例
如图,在正方形ABCD中,△BEC是等边三角形.求证:∠EAD=∠EDA=15°.
运用定理,解决问题
B
A
E
C
D
B
A
E
C
D
正方形
∠EAD,∠EDA
等边三角形
三条边都相等
三个角都是60°
四条边都相等
四个角都是直角
∠BAE,∠CDE
证明:∵
△BEC是等边三角形,
∴
BE=CE=BC,∠EBC=∠ECB=60°.
∵
四边形ABCD是正方形,
∴
AB=BC=CD,
∠ABC=∠BCD=∠DAB=90°.
∴
AB=BE=CE=CD,∠ABE=∠DCE=30°.
∴
△ABE,△DCE是等腰三角形.
B
A
E
C
D
∴
∠BAE=∠BEA=75°.
∴
∠EAD=∠DAB-∠BAE
=15°.
同理
∠EDA=15°.
∴
∠EAD=∠EDA=15°.
B
A
E
C
D
例题小结
正方形
应用正方形的性质
解决角度问题
挖掘隐含条件
例
如图,在Rt△ABC中,∠ACB=90°,CD平分∠ACB且交AB于点D,DE⊥BC于点E,DF⊥AC于点F.求证:四边形CEDF是正方形.
B
C
A
F
E
D
B
C
A
F
E
直角
DE⊥BC
DF⊥AC
四边形CEDF是正方形
矩形
对角线互相垂直
有一组邻边相等
D
B
C
A
F
E
在判定四边形CEDF是矩形后,证明对角线互相垂直.
角的平分线
∠CGE=90°
45°
1
2
3
对角线相等且互相平分
D
G
证明:∵
CD平分∠ACB,DE⊥BC,DF⊥AC,
∴
DE=DF,∠DFC=∠DEC=90
°.
又
∠ACB=90°,
∴
四边形CEDF是矩形.
又
DE=DF,
∴
四边形CEDF是正方形.
B
C
A
F
E
D
例题小结
正方形
有一组邻边相等
对角线互相垂直
有一个角是直角
对角线相等
平行四边形
矩形
菱形
练习
如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为
.
课堂练习,加深认识
C
A
B
D
E
1
2
正方形的面积
正方形的边长
正方形的性质
∠B=90°
勾股定理
C
A
B
D
E
正方形的性质
边长及面积
C
A
B
D
E
练习
如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为
.
3
练习
判断下列说法是否正确.
(1)正方形一定是矩形.
( )
(2)四条边都相等的四边形是正方形.
( )
(3)有一个角是直角的平行四边形是正方形.
( )
(4)两条对角线相等且互相垂直平分的四边形是正方
形.(
)
(5)两条对角线相等的菱形是正方形.
( )
√
×
×
练习
判断下列说法是否正确.
(1)正方形一定是矩形.
( )
(2)四条边都相等的四边形是正方形.
( )
(3)有一个角是直角的平行四边形是正方形.
( )
√
平行四边形
矩形
菱形
(4)两条对角线相等且互相垂直平分的四边形是正方形.(
)
√
平行四边形
矩形
(5)两条对角线相等的菱形是正方形.
( )
正方形
平行四边形
矩形
菱形
A
C
B
D
F
E
M
N
练习
如图,E,F,M,N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN.求证:四边形EFMN是正方形.
A
C
B
D
F
E
M
N
正方形ABCD
全等三角形
AE=BF=CM=DN
四个角都是直角,
四条边都相等
菱形EFMN
A
C
B
D
F
E
M
N
四边形EFMN是正方形
菱形EFMN
∠ANE=∠BEF
有一个角是直角
∠NEF=90°
证明:∵
四边形ABCD是正方形,
∴
AB=BC=CD=DA,
∠A=∠B=∠C=∠D=90°.
∵
AE=BF=CM=DN,
∴
AN=BE=CF=DM.
∴
△AEN≌△BFE≌△CMF≌△DNM.
A
C
B
D
F
E
M
N
∴
EN=FE=MF=NM,∠ANE=∠BEF.
∵
∠AEN+∠ANE=90°,
∴
∠AEN+∠BEF=90°.
∴
∠NEF=180°-∠AEN-∠BEF=90°.
∴
四边形EFMN是菱形.
∴
四边形EFMN是正方形.
A
C
B
D
F
E
M
N
定义
归纳总结,提升认识
判定
先证明矩形
再证明菱形
先证明菱形
再证明矩形
正方形
性
质
边
角
对角线
平行四边形
一般
特殊
矩形
菱形
正方形
课后作业
如图,在正方形ABCD的外侧,作等边三角形ADE,则∠AEB为(
).
(A)10°
(B)15°
(C)20°
(D)125°
A
B
E
D
C
2.
满足下列条件的四边形是不是正方形?为什么?
(1)对角线互相垂直且相等的平行四边形;
(2)对角线互相垂直的矩形;
(3)对角线相等的菱形;
(4)对角线互相垂直平分相等的四边形.
3.
如图,ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,测量知,EC=30m,EB=10m.这块场地的面积和对角线长分别是多少?
A
C
B
D
E
同学们再见!
正方形(第二课时)
初二年级
数学
定义
复习引入,回顾知识
正方形
有一组邻边相等的矩形是正方形.
有一个角是直角的菱形是正方形.
有一个角是直角且有一组邻边相等的平行四边形是正方形.
正方形的定义
定义
类比
正方形
性
质
边
角
对角线
正方形的四条边都相等.
正方形的四个角都是直角.
正方形的对角线相等,并且互相垂直平分.
正方形的性质
定义
判定
类比
正方形
性
质
边
角
对角线
正方形的判定
平行四边形
先判定矩形
再判定菱形
先判定菱形
再判定矩形
正方形
平行四边形
一般
特殊
矩形
菱形
正方形
四边形
平行四边形
矩形
正方形
菱形
综合运用,解决问题
图中共有多少个等腰直角三角形?
B
C
A
D
O
练习
如图,四边形ABCD是正方形,对角线AC,BD相交于点O.
分析:
B
C
A
D
O
OA=OB=OC=OD,AC⊥BD
△AOB,△BOC,△COD,△DOA
B
C
A
D
O
分析:
AB=BC=CD=DA,
∠ABC=∠BCD=∠CDA=∠DAB=90°
△ABC,△BCD,△CDA,△DAB
B
C
A
D
O
△AOB≌△BOC≌△COD≌△DOA
△ABC≌△BCD≌△CDA≌△DAB
解:图中一共有8个等腰直角三角形.
△AOB,△BOC,△COD,△DOA
△ABC,△BCD,△CDA,△DAB
全等三角形
45°
等腰直角三角形
全等三角形
特殊的角度
小结
B
C
A
D
O
如图,正方形ABCD两条对角线相交于点O,AB=2.
(1)对角线AC的长为
.
(2)△AOB的面积为
.
练习
B
C
A
D
O
2
等腰直角三角形
正方形
A
B
C
2
2
分析:
B
C
A
D
O
如图,正方形ABCD两条对角线相交于点O,AB=2.
(1)对角线AC的长为
.
(2)△AOB的面积为
.
B
C
A
D
O
2
全等三角形
正方形
方法1
B
C
A
D
O
2
等腰直角三角形
正方形
方法2
2
2
A
B
C
O
B
C
A
D
O
如图,正方形ABCD两条对角线相交于点O,AB=2.
(1)对角线AC的长为
.
(2)△AOB的面积为
.
1
小结
等腰直角三角形
勾股定理
线段的长
小结
等腰直角三角形
勾股定理
线段的长
例
如图,四边形ABCD是正方形,点E,F分别在AB,AD上,且BE=AF,BF与CE相交于点G.CE与BF相等吗?它们有什么位置关系?为什么?
A
B
C
D
F
E
G
猜想
CE=BF,CE⊥BF.
例
如图,四边形ABCD是正方形,点E,F分别在AB,AD上,且BE=AF,BF与CE相交于点G.CE与BF相等吗?它们有什么位置关系?为什么?
A
B
C
D
F
E
G
CE与BF的关系
分析:
△BCE≌△ABF
例
如图,四边形ABCD是正方形,点E,F分别在AB,AD上,且BE=AF,BF与CE相交于点G.CE与BF相等吗?它们有什么位置关系?为什么?
A
B
C
D
F
E
G
CE与BF的关系
△BCE≌△ABF
四边形ABCD是正方形
分析:
解:
CE=BF,CE⊥BF.
证明:∵
四边形ABCD是正方形,
∴
∠ABC=∠A=90°,BC=AB.
又
BE=AF,
∴
△BCE≌△ABF.
∴
CE=BF,∠1=∠2.
1
2
A
B
C
D
F
E
G
∵
∠1+∠3=90°,
∴
∠2+∠3=90°.
∴
∠BGC=90°.
∴
CE⊥BF
.
1
2
3
A
B
C
D
F
E
G
正方形的性质
全等三角形
线段的关系
A
B
C
D
F
E
G
对应边相等
对应角相等
A
B
C
D
F
E
G
小结
正方形的性质
全等三角形
线段的关系
A
B
C
D
F
E
G
对应边相等
对应角相等
A
B
C
D
F
E
G
小结
M
N
A
B
C
D
E
G
如图,四边形ABCD是正方形,点E,M,N分别在AB,BC,AD上,CE⊥MN
于点G.求证:CE=MN.
A
B
C
D
F
E
G
F
变式1
M
N
A
B
C
D
E
G
变式1
如图,四边形ABCD是正方形,点E,M,N分别在AB,BC,AD上,CE⊥MN
于点G.求证:CE=MN.
CE=BF
CE=MN
BF=MN
分析:
F
△BCE≌△ABF
∠ABC=∠A=90°
BC=AB
正方形的性质
M
N
A
B
C
D
E
G
变式1
如图,四边形ABCD是正方形,点E,M,N分别在AB,BC,AD上,CE⊥MN
于点G.求证:CE=MN.
分析:
F
CE=BF
CE=MN
BF=MN
△BCE≌△ABF
∠ABC=∠A=90°
BC=AB
正方形的性质
Q
2
1
3
∠1=∠3
M
N
A
B
C
D
E
G
变式1
如图,四边形ABCD是正方形,点E,M,N分别在AB,BC,AD上,CE⊥MN
于点G.求证:CE=MN.
分析:
F
CE=BF
CE=MN
BF=MN
△BCE≌△ABF
∠ABC=∠A=90°
BC=AB
正方形的性质
Q
2
1
3
∠1=∠3
?
BMNF
M
N
A
B
C
D
E
G
P
1
2
∠B=∠MPN
=90°
∠1=∠MCG
分析:
BC=PN
△BCE≌△PNM
∠B=∠MPN
=90°
∠1=∠MCG
分析:
M
N
A
B
C
D
E
G
P
1
2
证明:
过点B作BF⊥CE于点Q,交AD于点F.
∴
∠FQC=90°.
∴
∠1+∠2=90°.
∵
CE⊥MN,
∴
∠NGC=90°.
∴
∠NGC=∠FQC.
∴
BF∥MN.
M
N
A
B
C
D
E
G
F
Q
2
1
3
∵
四边形ABCD是正方形,
∴
BC=AB,∠ABC=∠A=90°,AD∥BC.
∴
∠2+∠3=90°.
∴
∠1=∠3.
∴
△BCE≌△ABF.
∴
CE=BF.
M
N
A
B
C
D
E
G
F
Q
2
1
3
M
N
A
B
C
D
E
G
F
Q
2
1
3
∵
BF∥MN,
AD∥BC
,
∴
四边形BMNF是平行四边形.
∴
BF=MN.
∴
CE=MN.
在正方形ABCD中
CE⊥MN
CE=MN
小结
M
N
A
B
C
D
E
G
F
添加辅助线
P
M
N
A
B
C
D
E
G
如图,四边形ABCD是正方形,点E在AB上,点H在AD的延长线上,CE⊥CH
于点C.求证:CE=CH.
A
B
C
D
F
E
G
H
A
B
C
D
E
F
分析:
变式2
变式2
如图,四边形ABCD是正方形,点E在AB上,点H在AD的延长线上,CE⊥CH
于点C.求证:CE=CH.
H
A
B
C
D
E
F
分析:
CE=BF
CE=CH
△BCE≌△ABF
∠ABC=∠A=90°
BC=AB
正方形的性质
∠BCE=∠ABF
变式2
如图,四边形ABCD是正方形,点E在AB上,点H在AD的延长线上,CE⊥CH
于点C.求证:CE=CH.
H
A
B
C
D
E
F
分析:
CE=CH
BF=CH
?
BCHF
CE=BF
△BCE≌△ABF
∠ABC=∠A=90°
BC=AB
正方形的性质
∠BCE=∠ABF
证明:
过点B作BF⊥CE于点Q,交AD于点F.
∴
∠FQC=90°.
∴
∠BCE+∠FBC=90°.
∵
CE⊥CH,
∴
∠HCE=90°.
∴
∠HCE+∠FQC=180°.
∴
BF∥CH.
Q
H
A
B
C
D
E
F
∵
四边形ABCD是正方形,
∴
BC=AB,∠ABC=∠A=90°,AD∥BC.
∴
∠ABF+∠FBC=90°.
∴
∠BCE=∠ABF.
∴
△BCE≌△ABF.
∴
CE=BF.
Q
H
A
B
C
D
E
F
∵
BF∥CH,
AD∥BC
,
∴
四边形BCHF是平行四边形.
∴
BF=CH.
∴
CE=CH.
Q
H
A
B
C
D
E
F
在正方形ABCD外部
CE⊥CH
CE=CH
小结
H
A
B
C
D
E
F
例题小结
A
B
C
D
F
E
F
A
B
C
D
F
E
M
N
A
B
C
D
E
H
图形的运动过程
线段的位置关系
添加辅助线
构造图形
例
如图,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,2).求B,C两点的坐标.
B
C
D
O
x
y
B,C两点的坐标
线段OB,BC
分析:
所在象限
确定符号
正方形性质
OB=OD
四条边相等
点B的横坐标
B
C
D
O
x
y
D
(0,2)
分析:
正方形性质
点C的坐标
CB⊥x轴,CD⊥y轴
B
C
D
O
x
y
OB的长
OD的长
分析:
点C的横坐标
点C的纵坐标
B
C
D
O
x
y
解:∵
四边形OBCD是正方形,
∴
CB⊥x轴,CD⊥y轴,OB=OD.
∵
点D的坐标是(0,2),
∴
OD=2.
∴
OB=OD=2.
∴
点B的坐标是(2,0).
∵
点C在第一象限,
∴
点C的坐标是(2,2).
例题小结
B
C
D
O
x
x
y
正方形的性质
点的坐标的含义
点的坐标
正方形
在坐标系中研究几何图形
几何图形的特征
坐标系的特征
解决问题
数形结合
例
如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,BE与对角线AC交于点P,连接DP.求DP+EP的值.
A
B
C
D
E
P
A
B
C
D
E
P
利用正方形的对称性
DP+EP
DP=BP
BP+EP
BE
例
如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,BE与对角线AC交于点P,连接DP.求DP+EP的值.
分析:
解:∵
AC是正方形ABCD的对角线,
∴
BP=DP.
∴
DP+EP=BP+EP=BE.
∵
△ABE是等边三角形,
∴
BE=AB.
∵
正方形ABCD的面积为16,
∴
AB=4.
∴
DP+EP=BE=4.
A
B
C
D
E
P
例题小结
正方形的轴对称性
线段的数量关系
四边形
平行四边形
矩形
正方形
菱形
归纳总结,提升认识
线段
等腰直角三角形
45°
B
C
A
D
O
45°
角
课后作业
如图,四边形ABCD是正方形.G是BC上的任意一点,DE⊥AG于点E,BF∥DE,且交AG于点F.
求证:AF-BF=EF.
A
B
C
D
E
F
G
2.
如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.求证:AE=EF.
A
B
C
D
E
F
同学们再见!
初二年级
数学
正方形(第一课时)
平行四边形
复习反思,引发思考
一般
特殊
以平行四边形为例,你能说一说如何研究一个几何图形吗?
菱形
矩形
平行四
边形
性
质
定义
边
判定
边
角
对角线
角
对角线
通过平行四边形边、角的特殊化,得到了特殊的平行四边形.
你能说说矩形、菱形与平行四边形有什么关系吗?
有一个角是直角
有一组邻边相等
两组对边
分别平行
四边形
平行四边形
矩形
菱形
有一个角是直角
两组对边
分别平行
四边形
平行四边形
矩形
菱形
正方形
有一组邻边相等
活动1
准备一张矩形的纸片,按照下图折叠,然后展开.
经验类比,得到定义
正方形
经验类比,得到定义
活动1
准备一张矩形的纸片,按照下图折叠,然后展开.
想一想:满足什么条件的矩形是正方形?
经验类比,得到定义
正方形
活动1
准备一张矩形的纸片,按照下图折叠,然后展开.
有一组邻边相等的矩形是正方形.
活动2
把可以活动的菱形框架的一个角变为直角.
想一想:满足什么条件的菱形是正方形?
活动2
把可以活动的菱形框架的一个角变为直角.
活动2
把可以活动的菱形框架的一个角变为直角.
有一个角是直角的菱形是正方形.
有一个角是直角
两组对边
分别平行
四边形
平行四边形
矩形
菱形
正方形
有一个角是直角
有一组邻边相等
有一个角是直角
有一组邻边相等
有一组邻边相等
正方形的定义
有一组邻边相等的矩形是正方形.
有一个角是直角的菱形是正方形.
有一个角是直角且有一组邻边相等的平行四边形是正方形.
正方形既是矩形,又是菱形.它具有矩形的性质,
又有菱形的性质.
B
C
A
D
O
你得到了哪些性质?
理性思考,获得定理
边
角
对角线
猜想1
正方形的四条边都相等.
四条边都相等
性质1
正方形的四条边都相等.
A
B
C
D
∵
四边形ABCD是正方形,
∴
AB=BC=CD=DA.
猜想2
正方形的四个角都是直角.
四个角都是直角
性质2
正方形的四个角都是直角.
A
B
C
D
∵
四边形ABCD是正方形,
∴
∠A=∠B=∠C=∠D=90°.
猜想:正方形的对角线相等,并且互相垂直平分.
已知:如图,四边形ABCD是正方形,对角线AC,BD相交于点O.
求证:AC=BD,AC⊥BD,AO=BO=CO=DO.
B
C
A
D
O
正方形
菱形
矩形
AC=BD
AC⊥BD
AO=CO,
BO=DO
AO=BO=CO=DO
证明:∵
正方形ABCD是矩形,
∴
AC=BD.
∵
正方形ABCD是平行四边形,
∴
AO=CO,BO=DO.
∴
AO=BO=CO=DO.
∵
正方形ABCD是菱形,
∴
AC⊥BD.
B
C
A
D
O
性质3
正方形的对角线相等,并且互相垂直平分.
∵
四边形ABCD是正方形,
∴
AC=BD,AC⊥BD,
AO=BO=CO=DO.
B
C
A
D
O
正方形是轴对称图形,它有四条对称轴,分别是对边中点的连线以及两条对角线所在的直线.
正方形是轴对称图形吗?
它的对称轴是什么?
对称性
B
C
A
D
O
正方形
边
角
对角线
矩形
四个角都是直角
对角线相等
菱形
四条边都相等
对角线互相垂直,并且每一条对角线平分一组对角
正方形的四条边都相等.
正方形的四个角都是直角.
正方形的对角线相等,并且互相垂直平分.
正方形的性质
用定义判定:
有一个角是直角且有一组邻边相等的平行四边形是正方形.
有一个角是直角的菱形是正方形.
有一组邻边相等的矩形是正方形.
矩形
菱形
正方形
有一组邻边相等
有一个角是直角
矩形
正方形
边
角
对角线
?
有一组邻边相等
猜想:对角线互相垂直的矩形是正方形.
已知:如图,四边形ABCD是矩形,对角线AC,BD相交于点O,AC⊥BD.
求证:四边形ABCD是正方形.
B
C
A
D
O
B
C
A
D
O
AC⊥BD
OB=OD
四边形ABCD是正方形
四边形ABCD是矩形
AB=AD
B
C
A
D
O
证明:∵
四边形ABCD是矩形,
∴
BO=DO.
∵
AC⊥BD,
∴
AB=AD.
∴
四边形ABCD是正方形.
判定
对角线互相垂直的矩形是正方形.
∵
四边形ABCD是矩形,AC⊥BD,
∴
四边形ABCD是正方形.
B
C
A
D
O
矩形
有一组邻边相等
对角线互相垂直
正方形
猜想:对角线相等的菱形是正方形.
已知:如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=BD.
求证:四边形ABCD是正方形.
B
C
A
D
O
B
C
A
D
O
AC=BD
四边形ABCD是正方形
四边形ABCD是菱形
四个等腰直角三角形
有一个角是直角
AO=CO,BO=DO,AC⊥BD
证明:∵
四边形ABCD是菱形,
∴
AO=CO,BO=DO,AC⊥BD.
∵
AC=BD,
∴
AO=BO=CO=DO.
∴
△AOD,△AOB是等腰直角三角形.
∴
∠BAO=∠DAO=45°.
∴
∠DAB=90°.
∴
四边形ABCD是正方形.
B
C
A
D
O
判定
对角线相等的菱形是正方形.
∵
四边形ABCD是菱形,AC=BD,
∴
四边形ABCD是正方形.
B
C
A
D
O
有一个角是直角
对角线相等
菱形
正方形
正方形的判定
平行四边形
先判定矩形
再判定菱形
先判定菱形
再判定矩形
正方形
例
如图,在正方形ABCD中,△BEC是等边三角形.求证:∠EAD=∠EDA=15°.
运用定理,解决问题
B
A
E
C
D
B
A
E
C
D
正方形
∠EAD,∠EDA
等边三角形
三条边都相等
三个角都是60°
四条边都相等
四个角都是直角
∠BAE,∠CDE
证明:∵
△BEC是等边三角形,
∴
BE=CE=BC,∠EBC=∠ECB=60°.
∵
四边形ABCD是正方形,
∴
AB=BC=CD,
∠ABC=∠BCD=∠DAB=90°.
∴
AB=BE=CE=CD,∠ABE=∠DCE=30°.
∴
△ABE,△DCE是等腰三角形.
B
A
E
C
D
∴
∠BAE=∠BEA=75°.
∴
∠EAD=∠DAB-∠BAE
=15°.
同理
∠EDA=15°.
∴
∠EAD=∠EDA=15°.
B
A
E
C
D
例题小结
正方形
应用正方形的性质
解决角度问题
挖掘隐含条件
例
如图,在Rt△ABC中,∠ACB=90°,CD平分∠ACB且交AB于点D,DE⊥BC于点E,DF⊥AC于点F.求证:四边形CEDF是正方形.
B
C
A
F
E
D
B
C
A
F
E
直角
DE⊥BC
DF⊥AC
四边形CEDF是正方形
矩形
对角线互相垂直
有一组邻边相等
D
B
C
A
F
E
在判定四边形CEDF是矩形后,证明对角线互相垂直.
角的平分线
∠CGE=90°
45°
1
2
3
对角线相等且互相平分
D
G
证明:∵
CD平分∠ACB,DE⊥BC,DF⊥AC,
∴
DE=DF,∠DFC=∠DEC=90
°.
又
∠ACB=90°,
∴
四边形CEDF是矩形.
又
DE=DF,
∴
四边形CEDF是正方形.
B
C
A
F
E
D
例题小结
正方形
有一组邻边相等
对角线互相垂直
有一个角是直角
对角线相等
平行四边形
矩形
菱形
练习
如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为
.
课堂练习,加深认识
C
A
B
D
E
1
2
正方形的面积
正方形的边长
正方形的性质
∠B=90°
勾股定理
C
A
B
D
E
正方形的性质
边长及面积
C
A
B
D
E
练习
如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为
.
3
练习
判断下列说法是否正确.
(1)正方形一定是矩形.
( )
(2)四条边都相等的四边形是正方形.
( )
(3)有一个角是直角的平行四边形是正方形.
( )
(4)两条对角线相等且互相垂直平分的四边形是正方
形.(
)
(5)两条对角线相等的菱形是正方形.
( )
√
×
×
练习
判断下列说法是否正确.
(1)正方形一定是矩形.
( )
(2)四条边都相等的四边形是正方形.
( )
(3)有一个角是直角的平行四边形是正方形.
( )
√
平行四边形
矩形
菱形
(4)两条对角线相等且互相垂直平分的四边形是正方形.(
)
√
平行四边形
矩形
(5)两条对角线相等的菱形是正方形.
( )
正方形
平行四边形
矩形
菱形
A
C
B
D
F
E
M
N
练习
如图,E,F,M,N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN.求证:四边形EFMN是正方形.
A
C
B
D
F
E
M
N
正方形ABCD
全等三角形
AE=BF=CM=DN
四个角都是直角,
四条边都相等
菱形EFMN
A
C
B
D
F
E
M
N
四边形EFMN是正方形
菱形EFMN
∠ANE=∠BEF
有一个角是直角
∠NEF=90°
证明:∵
四边形ABCD是正方形,
∴
AB=BC=CD=DA,
∠A=∠B=∠C=∠D=90°.
∵
AE=BF=CM=DN,
∴
AN=BE=CF=DM.
∴
△AEN≌△BFE≌△CMF≌△DNM.
A
C
B
D
F
E
M
N
∴
EN=FE=MF=NM,∠ANE=∠BEF.
∵
∠AEN+∠ANE=90°,
∴
∠AEN+∠BEF=90°.
∴
∠NEF=180°-∠AEN-∠BEF=90°.
∴
四边形EFMN是菱形.
∴
四边形EFMN是正方形.
A
C
B
D
F
E
M
N
定义
归纳总结,提升认识
判定
先证明矩形
再证明菱形
先证明菱形
再证明矩形
正方形
性
质
边
角
对角线
平行四边形
一般
特殊
矩形
菱形
正方形
课后作业
如图,在正方形ABCD的外侧,作等边三角形ADE,则∠AEB为(
).
(A)10°
(B)15°
(C)20°
(D)125°
A
B
E
D
C
2.
满足下列条件的四边形是不是正方形?为什么?
(1)对角线互相垂直且相等的平行四边形;
(2)对角线互相垂直的矩形;
(3)对角线相等的菱形;
(4)对角线互相垂直平分相等的四边形.
3.
如图,ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,测量知,EC=30m,EB=10m.这块场地的面积和对角线长分别是多少?
A
C
B
D
E
同学们再见!
正方形(第二课时)
初二年级
数学
定义
复习引入,回顾知识
正方形
有一组邻边相等的矩形是正方形.
有一个角是直角的菱形是正方形.
有一个角是直角且有一组邻边相等的平行四边形是正方形.
正方形的定义
定义
类比
正方形
性
质
边
角
对角线
正方形的四条边都相等.
正方形的四个角都是直角.
正方形的对角线相等,并且互相垂直平分.
正方形的性质
定义
判定
类比
正方形
性
质
边
角
对角线
正方形的判定
平行四边形
先判定矩形
再判定菱形
先判定菱形
再判定矩形
正方形
平行四边形
一般
特殊
矩形
菱形
正方形
四边形
平行四边形
矩形
正方形
菱形
综合运用,解决问题
图中共有多少个等腰直角三角形?
B
C
A
D
O
练习
如图,四边形ABCD是正方形,对角线AC,BD相交于点O.
分析:
B
C
A
D
O
OA=OB=OC=OD,AC⊥BD
△AOB,△BOC,△COD,△DOA
B
C
A
D
O
分析:
AB=BC=CD=DA,
∠ABC=∠BCD=∠CDA=∠DAB=90°
△ABC,△BCD,△CDA,△DAB
B
C
A
D
O
△AOB≌△BOC≌△COD≌△DOA
△ABC≌△BCD≌△CDA≌△DAB
解:图中一共有8个等腰直角三角形.
△AOB,△BOC,△COD,△DOA
△ABC,△BCD,△CDA,△DAB
全等三角形
45°
等腰直角三角形
全等三角形
特殊的角度
小结
B
C
A
D
O
如图,正方形ABCD两条对角线相交于点O,AB=2.
(1)对角线AC的长为
.
(2)△AOB的面积为
.
练习
B
C
A
D
O
2
等腰直角三角形
正方形
A
B
C
2
2
分析:
B
C
A
D
O
如图,正方形ABCD两条对角线相交于点O,AB=2.
(1)对角线AC的长为
.
(2)△AOB的面积为
.
B
C
A
D
O
2
全等三角形
正方形
方法1
B
C
A
D
O
2
等腰直角三角形
正方形
方法2
2
2
A
B
C
O
B
C
A
D
O
如图,正方形ABCD两条对角线相交于点O,AB=2.
(1)对角线AC的长为
.
(2)△AOB的面积为
.
1
小结
等腰直角三角形
勾股定理
线段的长
小结
等腰直角三角形
勾股定理
线段的长
例
如图,四边形ABCD是正方形,点E,F分别在AB,AD上,且BE=AF,BF与CE相交于点G.CE与BF相等吗?它们有什么位置关系?为什么?
A
B
C
D
F
E
G
猜想
CE=BF,CE⊥BF.
例
如图,四边形ABCD是正方形,点E,F分别在AB,AD上,且BE=AF,BF与CE相交于点G.CE与BF相等吗?它们有什么位置关系?为什么?
A
B
C
D
F
E
G
CE与BF的关系
分析:
△BCE≌△ABF
例
如图,四边形ABCD是正方形,点E,F分别在AB,AD上,且BE=AF,BF与CE相交于点G.CE与BF相等吗?它们有什么位置关系?为什么?
A
B
C
D
F
E
G
CE与BF的关系
△BCE≌△ABF
四边形ABCD是正方形
分析:
解:
CE=BF,CE⊥BF.
证明:∵
四边形ABCD是正方形,
∴
∠ABC=∠A=90°,BC=AB.
又
BE=AF,
∴
△BCE≌△ABF.
∴
CE=BF,∠1=∠2.
1
2
A
B
C
D
F
E
G
∵
∠1+∠3=90°,
∴
∠2+∠3=90°.
∴
∠BGC=90°.
∴
CE⊥BF
.
1
2
3
A
B
C
D
F
E
G
正方形的性质
全等三角形
线段的关系
A
B
C
D
F
E
G
对应边相等
对应角相等
A
B
C
D
F
E
G
小结
正方形的性质
全等三角形
线段的关系
A
B
C
D
F
E
G
对应边相等
对应角相等
A
B
C
D
F
E
G
小结
M
N
A
B
C
D
E
G
如图,四边形ABCD是正方形,点E,M,N分别在AB,BC,AD上,CE⊥MN
于点G.求证:CE=MN.
A
B
C
D
F
E
G
F
变式1
M
N
A
B
C
D
E
G
变式1
如图,四边形ABCD是正方形,点E,M,N分别在AB,BC,AD上,CE⊥MN
于点G.求证:CE=MN.
CE=BF
CE=MN
BF=MN
分析:
F
△BCE≌△ABF
∠ABC=∠A=90°
BC=AB
正方形的性质
M
N
A
B
C
D
E
G
变式1
如图,四边形ABCD是正方形,点E,M,N分别在AB,BC,AD上,CE⊥MN
于点G.求证:CE=MN.
分析:
F
CE=BF
CE=MN
BF=MN
△BCE≌△ABF
∠ABC=∠A=90°
BC=AB
正方形的性质
Q
2
1
3
∠1=∠3
M
N
A
B
C
D
E
G
变式1
如图,四边形ABCD是正方形,点E,M,N分别在AB,BC,AD上,CE⊥MN
于点G.求证:CE=MN.
分析:
F
CE=BF
CE=MN
BF=MN
△BCE≌△ABF
∠ABC=∠A=90°
BC=AB
正方形的性质
Q
2
1
3
∠1=∠3
?
BMNF
M
N
A
B
C
D
E
G
P
1
2
∠B=∠MPN
=90°
∠1=∠MCG
分析:
BC=PN
△BCE≌△PNM
∠B=∠MPN
=90°
∠1=∠MCG
分析:
M
N
A
B
C
D
E
G
P
1
2
证明:
过点B作BF⊥CE于点Q,交AD于点F.
∴
∠FQC=90°.
∴
∠1+∠2=90°.
∵
CE⊥MN,
∴
∠NGC=90°.
∴
∠NGC=∠FQC.
∴
BF∥MN.
M
N
A
B
C
D
E
G
F
Q
2
1
3
∵
四边形ABCD是正方形,
∴
BC=AB,∠ABC=∠A=90°,AD∥BC.
∴
∠2+∠3=90°.
∴
∠1=∠3.
∴
△BCE≌△ABF.
∴
CE=BF.
M
N
A
B
C
D
E
G
F
Q
2
1
3
M
N
A
B
C
D
E
G
F
Q
2
1
3
∵
BF∥MN,
AD∥BC
,
∴
四边形BMNF是平行四边形.
∴
BF=MN.
∴
CE=MN.
在正方形ABCD中
CE⊥MN
CE=MN
小结
M
N
A
B
C
D
E
G
F
添加辅助线
P
M
N
A
B
C
D
E
G
如图,四边形ABCD是正方形,点E在AB上,点H在AD的延长线上,CE⊥CH
于点C.求证:CE=CH.
A
B
C
D
F
E
G
H
A
B
C
D
E
F
分析:
变式2
变式2
如图,四边形ABCD是正方形,点E在AB上,点H在AD的延长线上,CE⊥CH
于点C.求证:CE=CH.
H
A
B
C
D
E
F
分析:
CE=BF
CE=CH
△BCE≌△ABF
∠ABC=∠A=90°
BC=AB
正方形的性质
∠BCE=∠ABF
变式2
如图,四边形ABCD是正方形,点E在AB上,点H在AD的延长线上,CE⊥CH
于点C.求证:CE=CH.
H
A
B
C
D
E
F
分析:
CE=CH
BF=CH
?
BCHF
CE=BF
△BCE≌△ABF
∠ABC=∠A=90°
BC=AB
正方形的性质
∠BCE=∠ABF
证明:
过点B作BF⊥CE于点Q,交AD于点F.
∴
∠FQC=90°.
∴
∠BCE+∠FBC=90°.
∵
CE⊥CH,
∴
∠HCE=90°.
∴
∠HCE+∠FQC=180°.
∴
BF∥CH.
Q
H
A
B
C
D
E
F
∵
四边形ABCD是正方形,
∴
BC=AB,∠ABC=∠A=90°,AD∥BC.
∴
∠ABF+∠FBC=90°.
∴
∠BCE=∠ABF.
∴
△BCE≌△ABF.
∴
CE=BF.
Q
H
A
B
C
D
E
F
∵
BF∥CH,
AD∥BC
,
∴
四边形BCHF是平行四边形.
∴
BF=CH.
∴
CE=CH.
Q
H
A
B
C
D
E
F
在正方形ABCD外部
CE⊥CH
CE=CH
小结
H
A
B
C
D
E
F
例题小结
A
B
C
D
F
E
F
A
B
C
D
F
E
M
N
A
B
C
D
E
H
图形的运动过程
线段的位置关系
添加辅助线
构造图形
例
如图,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,2).求B,C两点的坐标.
B
C
D
O
x
y
B,C两点的坐标
线段OB,BC
分析:
所在象限
确定符号
正方形性质
OB=OD
四条边相等
点B的横坐标
B
C
D
O
x
y
D
(0,2)
分析:
正方形性质
点C的坐标
CB⊥x轴,CD⊥y轴
B
C
D
O
x
y
OB的长
OD的长
分析:
点C的横坐标
点C的纵坐标
B
C
D
O
x
y
解:∵
四边形OBCD是正方形,
∴
CB⊥x轴,CD⊥y轴,OB=OD.
∵
点D的坐标是(0,2),
∴
OD=2.
∴
OB=OD=2.
∴
点B的坐标是(2,0).
∵
点C在第一象限,
∴
点C的坐标是(2,2).
例题小结
B
C
D
O
x
x
y
正方形的性质
点的坐标的含义
点的坐标
正方形
在坐标系中研究几何图形
几何图形的特征
坐标系的特征
解决问题
数形结合
例
如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,BE与对角线AC交于点P,连接DP.求DP+EP的值.
A
B
C
D
E
P
A
B
C
D
E
P
利用正方形的对称性
DP+EP
DP=BP
BP+EP
BE
例
如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,BE与对角线AC交于点P,连接DP.求DP+EP的值.
分析:
解:∵
AC是正方形ABCD的对角线,
∴
BP=DP.
∴
DP+EP=BP+EP=BE.
∵
△ABE是等边三角形,
∴
BE=AB.
∵
正方形ABCD的面积为16,
∴
AB=4.
∴
DP+EP=BE=4.
A
B
C
D
E
P
例题小结
正方形的轴对称性
线段的数量关系
四边形
平行四边形
矩形
正方形
菱形
归纳总结,提升认识
线段
等腰直角三角形
45°
B
C
A
D
O
45°
角
课后作业
如图,四边形ABCD是正方形.G是BC上的任意一点,DE⊥AG于点E,BF∥DE,且交AG于点F.
求证:AF-BF=EF.
A
B
C
D
E
F
G
2.
如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.求证:AE=EF.
A
B
C
D
E
F
同学们再见!
