人教版七年级数学下册课件8.4三元一次方程组解法及其应用(共28张PPT)
文档属性
| 名称 | 人教版七年级数学下册课件8.4三元一次方程组解法及其应用(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 464.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-04 21:55:52 | ||
图片预览








文档简介
(共28张PPT)
8.4
三元一次方程组
解法及其应用
1.下列不是二元一次方程组的是(
)
A
B
C
D
C
温故知新
2.解二元一次方程组:
3.二元一次方程组的三要素是什么?
解二元一次方程组的基本思路是什么?
化二元为一元
转化思想
代入消元法和加减消元法
学习目标:
(1)了解三元一次方程组的概念;
(2)能解简单的三元一次方程组,在解的过程中进一步体会“消元”思想.
(3)能利用三元一次方程组解决生活中的实际问题
学习重点:
会用消元法解三元一次方程组.
目标导航
三个小动物年龄之和为26岁
流氓兔比加菲猫大1岁
流氓兔年龄的2倍加上米老鼠的年龄之和比加菲猫大18岁
求
三
个
小
动
物
的年
龄
情境导入
探究一
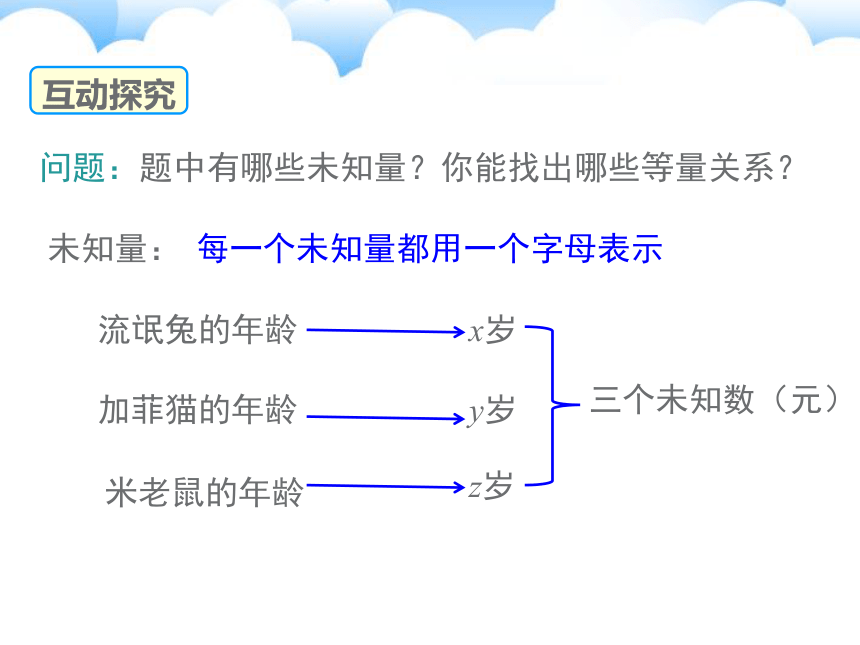
互动探究
问题:题中有哪些未知量?你能找出哪些等量关系?
未知量:
流氓兔的年龄
加菲猫的年龄
米老鼠的年龄
每一个未知量都用一个字母表示
x岁
y岁
z岁
三个未知数(元)
等量关系:
(1)流氓兔的年龄+加菲猫的年龄+米老鼠的年龄=26
(2)流氓兔的年龄=加菲猫的年龄+1
(3)2×流氓兔的年龄+米老鼠的年龄=加菲猫的年龄+18
用方程表示等量关系.
x+y+z=26.
?
x=y+1.
?
2x+z=y+18.
?
因三个小动物的年龄必须同时满足上述三个方程,故将三个方程联立在一起.
x+y+z=26.
?
x=y+1.
?
2x+z=y+18.
?
小明手头有12张面额分别是1元、2元、5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍.求1元、2元、5元的纸币各多少张?
问题中含有几个未知数?有
几个相等关系?
探索新知
探究二
设1元、2元、5元的纸币分别为x张、y张、z张.
根据题意,可以得到下面三个方程:
x+y+z=12
x=4y
x+2y+5z=22
①
②
③
你能根据等量关系列出方程吗?
交流探索
这个问题的解必须同时满足上面三个条件,因此,我们把这三个方程合在一起,写成
x+y+z=12,
x=4y,
x+2y+5z=22.
x+y+z=12
x+2y+5z=22
含有三个未知数,并且含有未知数的项的次数都是1,像这样的整式方程叫做三元一次方程.
x+y+z=26.
2x+z=y+18.
观察这四个方程,它们有什么共同的特点?
你能为它们命一个统一的名字吗?
你能依据二元一次方程的定义给出三元一次方程的定义吗?
新知探究
三元一次方程的定义:
一
观察上述两个方程组,想一想这两个方程组能叫做三元一次方程组吗?
x+y+z=12,
x=4y,
x+2y+5z=22.
方程组中含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个整式方程,像这样的方程组叫做三元一次方程组.
x+y+z=26.
?
x-1=y.
?
2x+z=y+18.
?
新知探究
请你类比二元一次方程组的定义给三元一次方程组下个定义.
三元一次方程组的定义:
二
跟踪训练
1.下列方程组中,不是三元一次方程组的是(
)
A.
B.
C.
D.
B
2.判断下列方程组是不是三元一次方程组?
方程个数不一定是三个,但至少要有两个。
方程中含有未知数的项的次数都是一次,而2xy是二次
方程中含有未知数的个数只有两个
√
×
×
√
简单三元一次方程组
跟踪训练
三元一次方程组的解:
三
类似二元一次方程组的解,三元一次方程组中各个方程的公共解,叫做这个三元一次方程组的解.
怎样解三元一次方程组呢?
能不能像以前一样“消元”,把“三元”化成“二元”呢?
①
③
②
解:把②分别代入①③得:
5y+z=12
④
6y+5z=22
⑤
由④得z=12-5y
把z=12-5y代入⑤得:
6y+5(12-5y)=22
解得
y=2
由②得x=8
把y=2,x=8
分别代入
①
得:
2+8+z=12
z=2
∴原方程组的解是
代入法
消x
新知探究
解三元一次方程组:
你还有其它方法吗?
①
②
③
解:
①
×5-
③得:4x+3y=38④
把x=4y代入④得:y=2
x=8
把y=2,x=8分别代入
①得:
2+8+z=12
z=2
∴原方程组的解是
加减法
消z
新知探究
解三元一次方程组:
解三元一次方程组的基本思路是:
通过“代入”或“加减”进行消元,把“三元”转化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而再转化为解一元一次方程。
三元一次方程组
消元
二元一次方程组
消元
一元一次方程
新知探究
解:②×3+③
,得
11x+10z=35
④
①与④组成方程组
解这个方程组,得
把x=5,z=-2代入②,得y=
因此,这个三元一次方程组的解为
3x+4z=7,
11x+10z=35.
x=5,
z=-2.
3x+4z=7,
①
2x+3y+z=9,
②
5x-9y+7z=8.
③
x=5,
y=
z=-2.
典例精析
【例1】解三元一次方程组:
例2
在等式
中,当
时,
;当
时,
;当
时,
求
的值.
分析:根据已知条件,你能得到什么?
典例精析
解:根据题意,
得三元一次方程组
②-①,得a+b=1;
④
③-①,得4a+b=10;
⑤
④与⑤组成二元一次方程组
解这个方程组,得
①
②
③
代入①,得
c=-5
因此,
答:
典例精析
例3.解三元一次方程组
你准备消去哪个未知数?
你有几种消元方案?试一试!
典例精析
方案一:
(消x)
由②得x=1+y分别代入①、③得到
关于y
、z的二元一次方程:
方案二:
(消y)由②得y=x-1分别代入①、③得到关于x、z的二元一次方程组:
方案三:(消z)由①得z=23-x-y代入③得到关于x、y的二元一次方程,此方程与②联立成关于x、y的二元一次方程组。
例3.解三元一次方程组
你准备消去哪个未知数?
你有几种消元方案?试一试!
典例精析
方案一:(消x)①
-
②消x,
得含y、z的二元一次方程。
①
×2-
③消x,得含y、z的二元一次方程。
方案二:(消y)①+
②消y,
得含x、z的二元一次方程。
②+
③消y,
得含x、z的二元一次方程。
方案三:(消z)①
+
③消z,
得含x、y的二元一次方程,
与②联立成关于x、y的二元一次方程组。
一元一次方程
求出第一个未知数的值
求出第三个未知数的值
求出第二个未知数的值
二元一次方程组
三元一次方程组
小结:
谈谈你有哪些收获?
三元一次方程的解题思路是什么?
1.消元时一般先消去系数
的未知数;
2.如果三个方程中有一个方程是二元一次方程,则可以先通过对另外两个方程组进行消元,消去二元一次方程中缺少的那个元(
);
3.消元时,每个方程至少要用一次;
4.有表达式“x=···,”
用
;
5.相同未知数系数相同或相反,
.
代入法
加减消元法
技巧小结:
最简单
缺某元,消某元
(2)解三元一次方程组的基本方法是代入法和加减法
,加减法比较常用.
(1)
解三元一次方程组的基本思想是消元,
关键也是消元。我们一定要根据方程组的特点,选准消元对象,
定好消元方案.
(3)
解完后要代入原方程组的三个方程中进行检验.
教师总结
1.解方程组
若要使运算简便,消元的方
法应选取(
)
(A)先消去x;
(B)先消去y;
(C)先消去z;
(D)以上说法都不对.
巩固训练
B
2.解下列三元一次方程组
.
3.甲、乙、丙三个数的和是35,甲数的2倍比乙数大5,乙
数的三分之一等于丙数的二分之一.求这三个数.
4.甲、乙、丙三个数的和是35,甲数的2倍比乙数大5,乙数的
等于丙数的
。求这三个数。
巩固训练
5.一个三位数,个位、百位上的数的和等于十位上的数,百位上的数的7倍比个位、十位上的数的和大2,且个位、十位、百位上的数的和是14.求这个三位数。
6.若|x-3y+5|+|3x+y-5|+
=0,求x,y,z的值。
7.若x+2y+3z=10,4x+3y+2z=15,则x+y+z的值为(
)
A.2
B.3
C.4
D.5
8.4
三元一次方程组
解法及其应用
1.下列不是二元一次方程组的是(
)
A
B
C
D
C
温故知新
2.解二元一次方程组:
3.二元一次方程组的三要素是什么?
解二元一次方程组的基本思路是什么?
化二元为一元
转化思想
代入消元法和加减消元法
学习目标:
(1)了解三元一次方程组的概念;
(2)能解简单的三元一次方程组,在解的过程中进一步体会“消元”思想.
(3)能利用三元一次方程组解决生活中的实际问题
学习重点:
会用消元法解三元一次方程组.
目标导航
三个小动物年龄之和为26岁
流氓兔比加菲猫大1岁
流氓兔年龄的2倍加上米老鼠的年龄之和比加菲猫大18岁
求
三
个
小
动
物
的年
龄
情境导入
探究一
互动探究
问题:题中有哪些未知量?你能找出哪些等量关系?
未知量:
流氓兔的年龄
加菲猫的年龄
米老鼠的年龄
每一个未知量都用一个字母表示
x岁
y岁
z岁
三个未知数(元)
等量关系:
(1)流氓兔的年龄+加菲猫的年龄+米老鼠的年龄=26
(2)流氓兔的年龄=加菲猫的年龄+1
(3)2×流氓兔的年龄+米老鼠的年龄=加菲猫的年龄+18
用方程表示等量关系.
x+y+z=26.
?
x=y+1.
?
2x+z=y+18.
?
因三个小动物的年龄必须同时满足上述三个方程,故将三个方程联立在一起.
x+y+z=26.
?
x=y+1.
?
2x+z=y+18.
?
小明手头有12张面额分别是1元、2元、5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍.求1元、2元、5元的纸币各多少张?
问题中含有几个未知数?有
几个相等关系?
探索新知
探究二
设1元、2元、5元的纸币分别为x张、y张、z张.
根据题意,可以得到下面三个方程:
x+y+z=12
x=4y
x+2y+5z=22
①
②
③
你能根据等量关系列出方程吗?
交流探索
这个问题的解必须同时满足上面三个条件,因此,我们把这三个方程合在一起,写成
x+y+z=12,
x=4y,
x+2y+5z=22.
x+y+z=12
x+2y+5z=22
含有三个未知数,并且含有未知数的项的次数都是1,像这样的整式方程叫做三元一次方程.
x+y+z=26.
2x+z=y+18.
观察这四个方程,它们有什么共同的特点?
你能为它们命一个统一的名字吗?
你能依据二元一次方程的定义给出三元一次方程的定义吗?
新知探究
三元一次方程的定义:
一
观察上述两个方程组,想一想这两个方程组能叫做三元一次方程组吗?
x+y+z=12,
x=4y,
x+2y+5z=22.
方程组中含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个整式方程,像这样的方程组叫做三元一次方程组.
x+y+z=26.
?
x-1=y.
?
2x+z=y+18.
?
新知探究
请你类比二元一次方程组的定义给三元一次方程组下个定义.
三元一次方程组的定义:
二
跟踪训练
1.下列方程组中,不是三元一次方程组的是(
)
A.
B.
C.
D.
B
2.判断下列方程组是不是三元一次方程组?
方程个数不一定是三个,但至少要有两个。
方程中含有未知数的项的次数都是一次,而2xy是二次
方程中含有未知数的个数只有两个
√
×
×
√
简单三元一次方程组
跟踪训练
三元一次方程组的解:
三
类似二元一次方程组的解,三元一次方程组中各个方程的公共解,叫做这个三元一次方程组的解.
怎样解三元一次方程组呢?
能不能像以前一样“消元”,把“三元”化成“二元”呢?
①
③
②
解:把②分别代入①③得:
5y+z=12
④
6y+5z=22
⑤
由④得z=12-5y
把z=12-5y代入⑤得:
6y+5(12-5y)=22
解得
y=2
由②得x=8
把y=2,x=8
分别代入
①
得:
2+8+z=12
z=2
∴原方程组的解是
代入法
消x
新知探究
解三元一次方程组:
你还有其它方法吗?
①
②
③
解:
①
×5-
③得:4x+3y=38④
把x=4y代入④得:y=2
x=8
把y=2,x=8分别代入
①得:
2+8+z=12
z=2
∴原方程组的解是
加减法
消z
新知探究
解三元一次方程组:
解三元一次方程组的基本思路是:
通过“代入”或“加减”进行消元,把“三元”转化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而再转化为解一元一次方程。
三元一次方程组
消元
二元一次方程组
消元
一元一次方程
新知探究
解:②×3+③
,得
11x+10z=35
④
①与④组成方程组
解这个方程组,得
把x=5,z=-2代入②,得y=
因此,这个三元一次方程组的解为
3x+4z=7,
11x+10z=35.
x=5,
z=-2.
3x+4z=7,
①
2x+3y+z=9,
②
5x-9y+7z=8.
③
x=5,
y=
z=-2.
典例精析
【例1】解三元一次方程组:
例2
在等式
中,当
时,
;当
时,
;当
时,
求
的值.
分析:根据已知条件,你能得到什么?
典例精析
解:根据题意,
得三元一次方程组
②-①,得a+b=1;
④
③-①,得4a+b=10;
⑤
④与⑤组成二元一次方程组
解这个方程组,得
①
②
③
代入①,得
c=-5
因此,
答:
典例精析
例3.解三元一次方程组
你准备消去哪个未知数?
你有几种消元方案?试一试!
典例精析
方案一:
(消x)
由②得x=1+y分别代入①、③得到
关于y
、z的二元一次方程:
方案二:
(消y)由②得y=x-1分别代入①、③得到关于x、z的二元一次方程组:
方案三:(消z)由①得z=23-x-y代入③得到关于x、y的二元一次方程,此方程与②联立成关于x、y的二元一次方程组。
例3.解三元一次方程组
你准备消去哪个未知数?
你有几种消元方案?试一试!
典例精析
方案一:(消x)①
-
②消x,
得含y、z的二元一次方程。
①
×2-
③消x,得含y、z的二元一次方程。
方案二:(消y)①+
②消y,
得含x、z的二元一次方程。
②+
③消y,
得含x、z的二元一次方程。
方案三:(消z)①
+
③消z,
得含x、y的二元一次方程,
与②联立成关于x、y的二元一次方程组。
一元一次方程
求出第一个未知数的值
求出第三个未知数的值
求出第二个未知数的值
二元一次方程组
三元一次方程组
小结:
谈谈你有哪些收获?
三元一次方程的解题思路是什么?
1.消元时一般先消去系数
的未知数;
2.如果三个方程中有一个方程是二元一次方程,则可以先通过对另外两个方程组进行消元,消去二元一次方程中缺少的那个元(
);
3.消元时,每个方程至少要用一次;
4.有表达式“x=···,”
用
;
5.相同未知数系数相同或相反,
.
代入法
加减消元法
技巧小结:
最简单
缺某元,消某元
(2)解三元一次方程组的基本方法是代入法和加减法
,加减法比较常用.
(1)
解三元一次方程组的基本思想是消元,
关键也是消元。我们一定要根据方程组的特点,选准消元对象,
定好消元方案.
(3)
解完后要代入原方程组的三个方程中进行检验.
教师总结
1.解方程组
若要使运算简便,消元的方
法应选取(
)
(A)先消去x;
(B)先消去y;
(C)先消去z;
(D)以上说法都不对.
巩固训练
B
2.解下列三元一次方程组
.
3.甲、乙、丙三个数的和是35,甲数的2倍比乙数大5,乙
数的三分之一等于丙数的二分之一.求这三个数.
4.甲、乙、丙三个数的和是35,甲数的2倍比乙数大5,乙数的
等于丙数的
。求这三个数。
巩固训练
5.一个三位数,个位、百位上的数的和等于十位上的数,百位上的数的7倍比个位、十位上的数的和大2,且个位、十位、百位上的数的和是14.求这个三位数。
6.若|x-3y+5|+|3x+y-5|+
=0,求x,y,z的值。
7.若x+2y+3z=10,4x+3y+2z=15,则x+y+z的值为(
)
A.2
B.3
C.4
D.5
