沪教版高中数学高二下册第十二章12.4 椭圆的性质 课件(共17张PPT)
文档属性
| 名称 | 沪教版高中数学高二下册第十二章12.4 椭圆的性质 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 282.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-06 21:25:34 | ||
图片预览


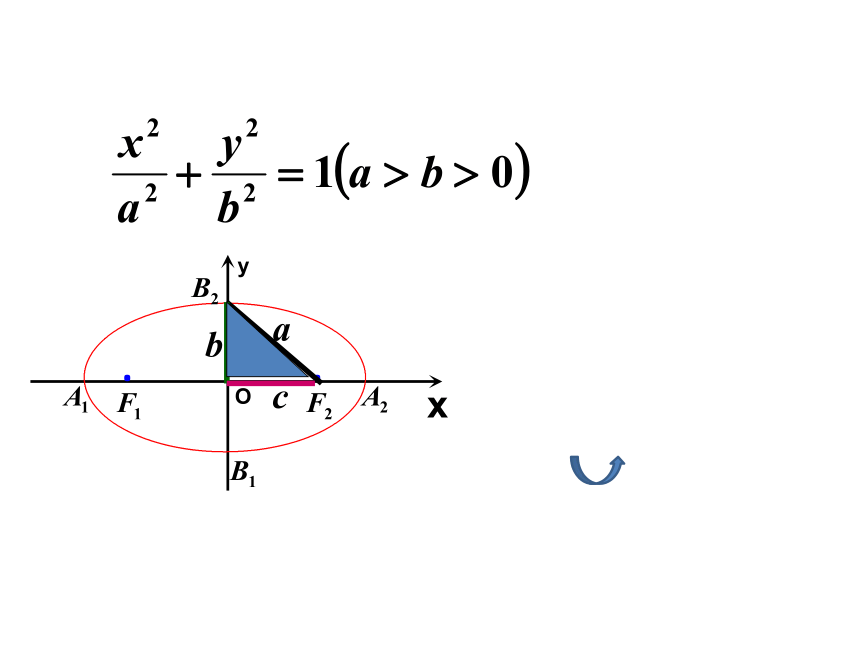



文档简介
(共17张PPT)
椭圆的性质
2020年6月2日
标准方程
图形
焦点坐标
定义
a、b、c的等量关系
焦点位置的判定
共同点
不同点
F1(-c,0)、F2(c,0)
F1(0,-c)、F2(0,c)
平面内与两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.
b2
=
a2
–c2
椭圆的两种标准方程中,总是
a>b>0.
所以哪个项的分母大,焦点就在那个轴上;反过来,焦点在哪个轴上,相应的那个项的分母就越大.
x
y
M
O
x
y
M
O
O
x
y
.
.
观察:
O
x
y
.
.
F1
F2
x
y
O
P(x,y)
Q(-x,-y)
N(x,-y)
M(-x,y)
1对称性
在标准方程下,
坐标轴是对称轴,
原点是对称中心,
椭圆的对称中心叫做椭圆的中心。
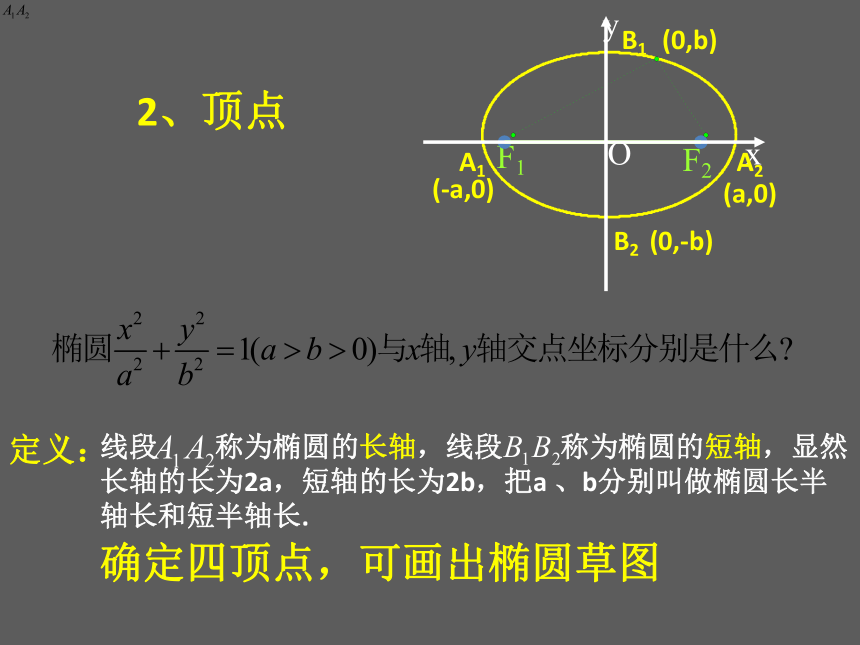
定义:
线段 称为椭圆的长轴,线段 称为椭圆的短轴,显然长轴的长为2a,短轴的长为2b,把a
、b分别叫做椭圆长半轴长和短半轴长.
F1
F2
x
y
O
A1
A2
B1
B2
(-a,0)
(a,0)
(0,b)
(0,-b)
确定四顶点,可画出椭圆草图
2、顶点
F1
F2
x
y
O
A1
A2
B1
B2
(-a,0)
(a,0)
(0,b)
(0,-b)
3、范围
说出椭圆
的对称性、顶点、范围;
F1
F2
M
x
y
O
O
x
y
.
.
P(x,y)
解:
O
x
y
.
.
标准方程
(
)
(
)
图形
性质
范围
对称性
关于
x轴、
y轴和原点对称
顶点
焦点
两轴
长轴长
,
短轴长
焦距
|F1F2|=2c,c2=a2-b2
作业:
练习册:P27,
A:T1,2,3,4,6,8,
B:T1,2,3
椭圆的性质
2020年6月2日
标准方程
图形
焦点坐标
定义
a、b、c的等量关系
焦点位置的判定
共同点
不同点
F1(-c,0)、F2(c,0)
F1(0,-c)、F2(0,c)
平面内与两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.
b2
=
a2
–c2
椭圆的两种标准方程中,总是
a>b>0.
所以哪个项的分母大,焦点就在那个轴上;反过来,焦点在哪个轴上,相应的那个项的分母就越大.
x
y
M
O
x
y
M
O
O
x
y
.
.
观察:
O
x
y
.
.
F1
F2
x
y
O
P(x,y)
Q(-x,-y)
N(x,-y)
M(-x,y)
1对称性
在标准方程下,
坐标轴是对称轴,
原点是对称中心,
椭圆的对称中心叫做椭圆的中心。
定义:
线段 称为椭圆的长轴,线段 称为椭圆的短轴,显然长轴的长为2a,短轴的长为2b,把a
、b分别叫做椭圆长半轴长和短半轴长.
F1
F2
x
y
O
A1
A2
B1
B2
(-a,0)
(a,0)
(0,b)
(0,-b)
确定四顶点,可画出椭圆草图
2、顶点
F1
F2
x
y
O
A1
A2
B1
B2
(-a,0)
(a,0)
(0,b)
(0,-b)
3、范围
说出椭圆
的对称性、顶点、范围;
F1
F2
M
x
y
O
O
x
y
.
.
P(x,y)
解:
O
x
y
.
.
标准方程
(
)
(
)
图形
性质
范围
对称性
关于
x轴、
y轴和原点对称
顶点
焦点
两轴
长轴长
,
短轴长
焦距
|F1F2|=2c,c2=a2-b2
作业:
练习册:P27,
A:T1,2,3,4,6,8,
B:T1,2,3
