沪教版高中数学高二下册第十二章12.8 抛物线的性质 课件(共15张PPT)
文档属性
| 名称 | 沪教版高中数学高二下册第十二章12.8 抛物线的性质 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 268.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-06 21:44:09 | ||
图片预览



文档简介
(共15张PPT)
抛物线的性质
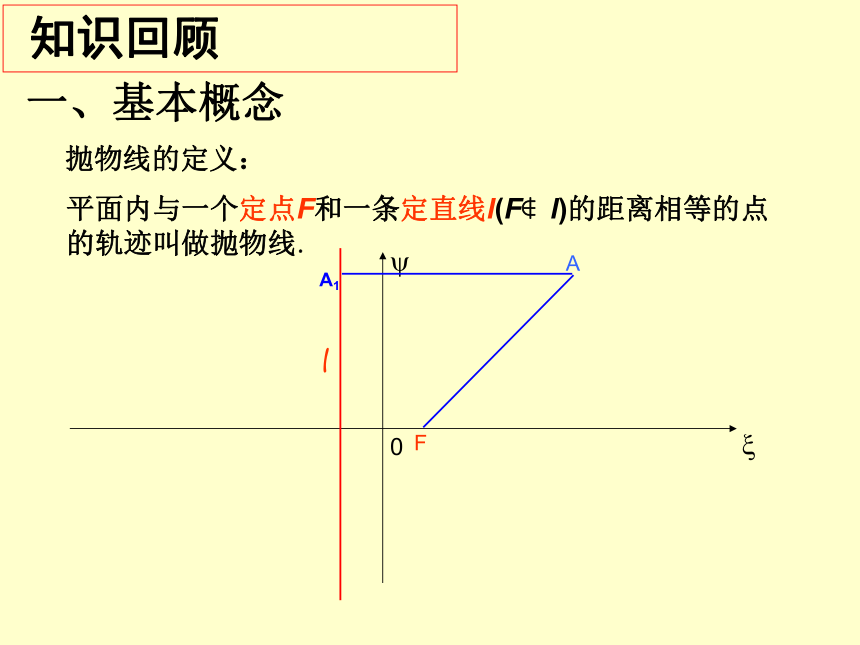
知识回顾
一、基本概念
抛物线的定义:
平面内与一个定点F和一条定直线l(F?l)的距离相等的点的轨迹叫做抛物线.
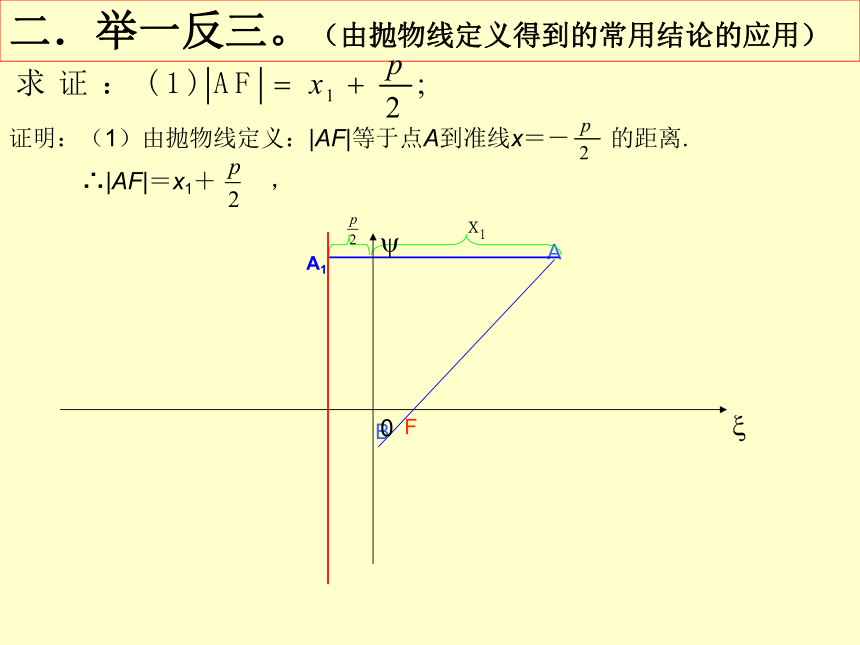
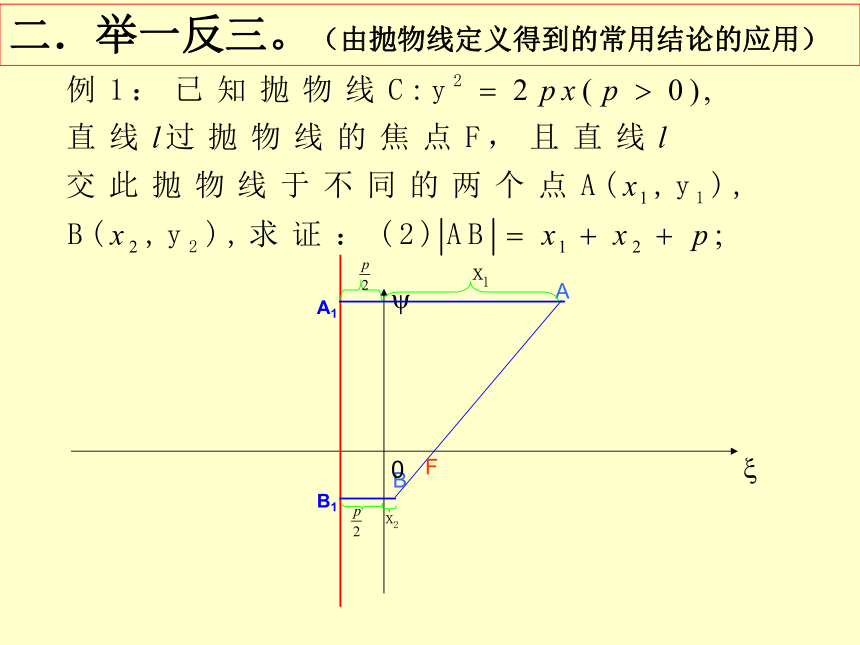
二.举一反三。(由抛物线定义得到的常用结论的应用)
二.举一反三。(由抛物线定义得到的常用结论的应用)
二.举一反三。(由抛物线定义得到的常用结论的应用)
二.举一反三。(由抛物线定义得到的常用结论的应用)
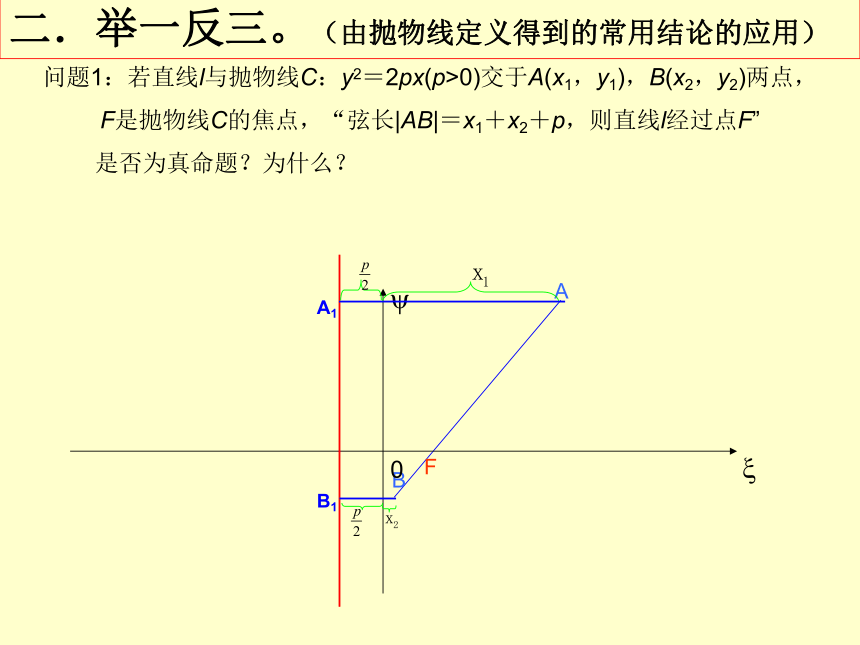
问题1:若直线l与抛物线C:y2=2px(p>0)交于A(x1,y1),B(x2,y2)两点,
F是抛物线C的焦点,“弦长|AB|=x1+x2+p,则直线l经过点F”
是否为真命题?为什么?
二.举一反三。(由抛物线定义得到的常用结论的应用)
问题2:已知抛物线y2=2px(p>0)的焦点为F,点P1(x1,y1)、P2(x2,y2)、
P3(x3,y3)在抛物线上,且2x2=x1+x3,则有
( )
A.|FP1|+|FP2|=|FP3|
B.|FP1|2+|FP2|2=|FP3|2
C.2|FP2|=|FP1|+|FP3|
D.|FP2|2=|FP1|·|FP3|
C
二.举一反三。(由抛物线定义得到的常用结论的应用)
二.举一反三。(由抛物线定义得到的常用结论的应用)
解:如图:因为抛物线的焦点为F(2,0),
所以|AB|=|AF|+|BF|
=
|AA1|+|BB2|
A
三.应用举例(过焦点的直线与抛物线相交)
例2:已知抛物线C:y2=2px(p>0),直线l过抛物线焦点F且直线l交此抛物线于不同的两个点A(x1,y1)、B(x2,y2),,
求证:
解:如图:因为抛物线的焦点
三.应用举例(过焦点的直线与抛物线相交)
例2:已知抛物线C:y2=2px(p>0),直线l过抛物线焦点F,且直线l交此抛物线于不同的两个点A(x1,y1)、B(x2,y2),
求证:
四.拓展提高。
(不过焦点的直线与抛物线相交)
例3:已知抛物线C:y2=2px(p>0),直线l交此抛物线于不同的两个点A(x1,y1)、B(x2,y2),且直线l过抛物线焦点F,
(1)直线l过点M(-p,0)时,证明:y1·y2为定值;
四.拓展提高。
(不过焦点的直线与抛物线相交)
例3:已知抛物线C:y2=2px(p>0),直线l交此抛物线于不同的两个点A(x1,y1)、B(x2,y2),且直线l过抛物线焦点F,
(2)当
y1·y2=-p时,直线l是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由。
五.思考分析。
(不过焦点的直线与抛物线相交)
例4:已知抛物线C:y2=2px(p>0),直线l交此抛物线于不同的两个点A(x1,y1)、B(x2,y2),且直线l过抛物线焦点F,
五.课堂小结。
六.作业布置。
谢
谢
抛物线的性质
知识回顾
一、基本概念
抛物线的定义:
平面内与一个定点F和一条定直线l(F?l)的距离相等的点的轨迹叫做抛物线.
二.举一反三。(由抛物线定义得到的常用结论的应用)
二.举一反三。(由抛物线定义得到的常用结论的应用)
二.举一反三。(由抛物线定义得到的常用结论的应用)
二.举一反三。(由抛物线定义得到的常用结论的应用)
问题1:若直线l与抛物线C:y2=2px(p>0)交于A(x1,y1),B(x2,y2)两点,
F是抛物线C的焦点,“弦长|AB|=x1+x2+p,则直线l经过点F”
是否为真命题?为什么?
二.举一反三。(由抛物线定义得到的常用结论的应用)
问题2:已知抛物线y2=2px(p>0)的焦点为F,点P1(x1,y1)、P2(x2,y2)、
P3(x3,y3)在抛物线上,且2x2=x1+x3,则有
( )
A.|FP1|+|FP2|=|FP3|
B.|FP1|2+|FP2|2=|FP3|2
C.2|FP2|=|FP1|+|FP3|
D.|FP2|2=|FP1|·|FP3|
C
二.举一反三。(由抛物线定义得到的常用结论的应用)
二.举一反三。(由抛物线定义得到的常用结论的应用)
解:如图:因为抛物线的焦点为F(2,0),
所以|AB|=|AF|+|BF|
=
|AA1|+|BB2|
A
三.应用举例(过焦点的直线与抛物线相交)
例2:已知抛物线C:y2=2px(p>0),直线l过抛物线焦点F且直线l交此抛物线于不同的两个点A(x1,y1)、B(x2,y2),,
求证:
解:如图:因为抛物线的焦点
三.应用举例(过焦点的直线与抛物线相交)
例2:已知抛物线C:y2=2px(p>0),直线l过抛物线焦点F,且直线l交此抛物线于不同的两个点A(x1,y1)、B(x2,y2),
求证:
四.拓展提高。
(不过焦点的直线与抛物线相交)
例3:已知抛物线C:y2=2px(p>0),直线l交此抛物线于不同的两个点A(x1,y1)、B(x2,y2),且直线l过抛物线焦点F,
(1)直线l过点M(-p,0)时,证明:y1·y2为定值;
四.拓展提高。
(不过焦点的直线与抛物线相交)
例3:已知抛物线C:y2=2px(p>0),直线l交此抛物线于不同的两个点A(x1,y1)、B(x2,y2),且直线l过抛物线焦点F,
(2)当
y1·y2=-p时,直线l是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由。
五.思考分析。
(不过焦点的直线与抛物线相交)
例4:已知抛物线C:y2=2px(p>0),直线l交此抛物线于不同的两个点A(x1,y1)、B(x2,y2),且直线l过抛物线焦点F,
五.课堂小结。
六.作业布置。
谢
谢
