沪教版高中数学高二下册第十二章小结:椭圆中与面积有关的取值范围问题 课件(共15张PPT)
文档属性
| 名称 | 沪教版高中数学高二下册第十二章小结:椭圆中与面积有关的取值范围问题 课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-07 10:58:04 | ||
图片预览




文档简介
(共15张PPT)
椭圆中与面积有关的
取值范围问题
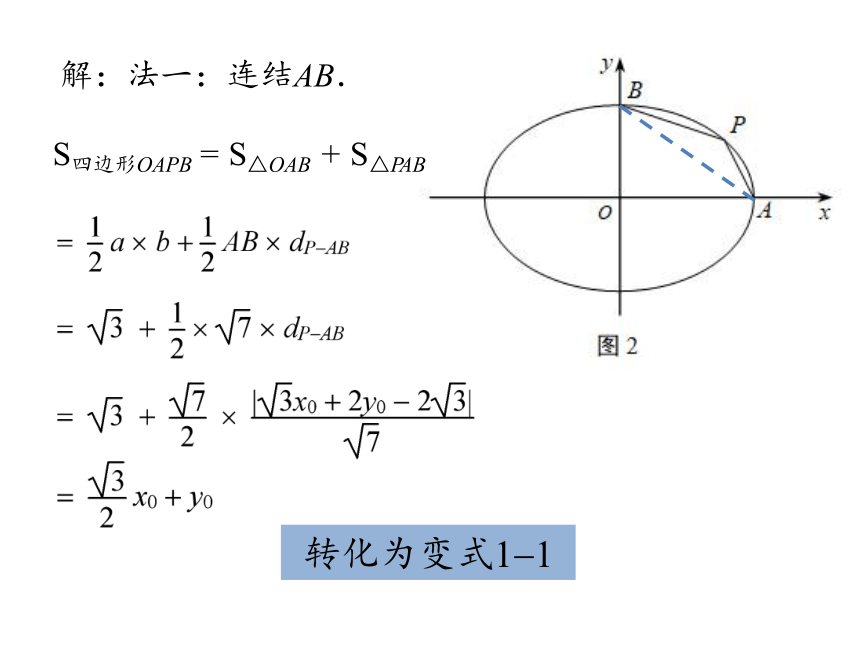
解:法一:连结AB.
S四边形OAPB
=
S△OAB
+
S△PAB
转化为变式1?1
法二:连结OP,设P(x0,
y0).
S四边形OAPB
=
S△OPB
+
S△OPA
法三:过P作P
G
?
x轴于点G.
S四边形OAPB
=
S四边形OGPB
+
S△PGA
G
问题转化为:
法一(运用基本不等式):
法二:
法三:
线性规划(方程思想)
作业拓展
总结
借助几何图形,寻找存在“最值”的特殊位置;
2.建立面积的目标函数,用代数方法求此函数的最值;
(引入变元—建模—解模)
3.识图能力,运算能力,数据处理能力;
4.化归思想、数形结合思想;
5.通过一题多解,一题多变体会数学解题中的和谐统一之美.
品
田园高中团委学生会
图1
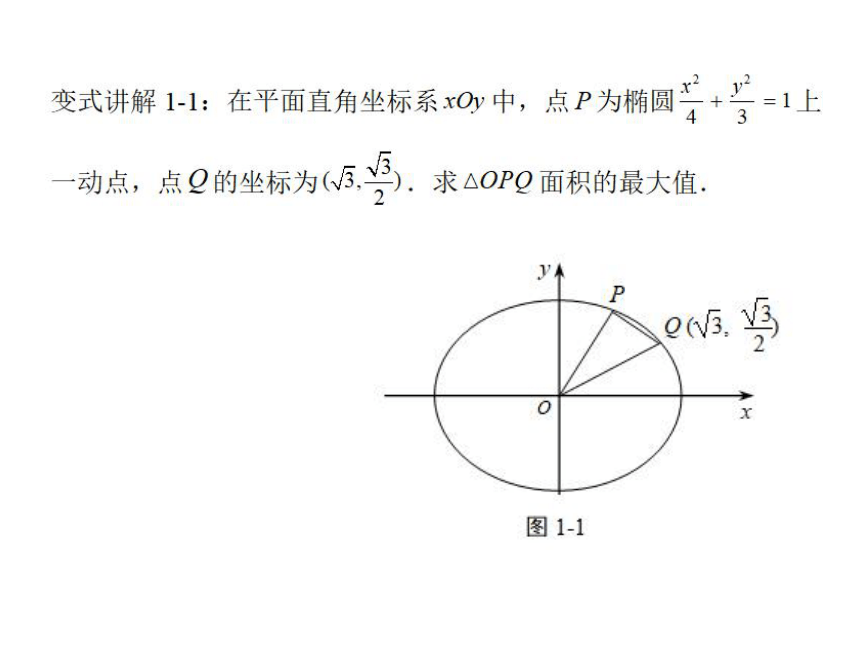
变式讲解1:在平面直角坐标系xOy中,点P为椭圆4+3=1上
动点,点Q的坐标为(3,).求△OPQ面积的最大值
Q
图1-1
变式讲解1:在平面直角坐标系xOy中,点P为椭圆x+=1上一动点,点Q的坐标为(3,y2)
4
求△OPQ面积的最大值
P
Q(3
解度P时第+,0+一
k=,直线0为和,昂y=0
=x-1l_△o-l
dp-ou++
45
图1-1
食十=第0代锅参),-08,和=130,0∈回可
十一08将8=40+),叶含∈,)
于
te[4So最大值为书
⊙线性划(推程鼠想),=%-士t
由{+4们=,际4)-=+x+已=04-4-6)=P(-+≥0
=X。-t
-4≤t≤4.
B
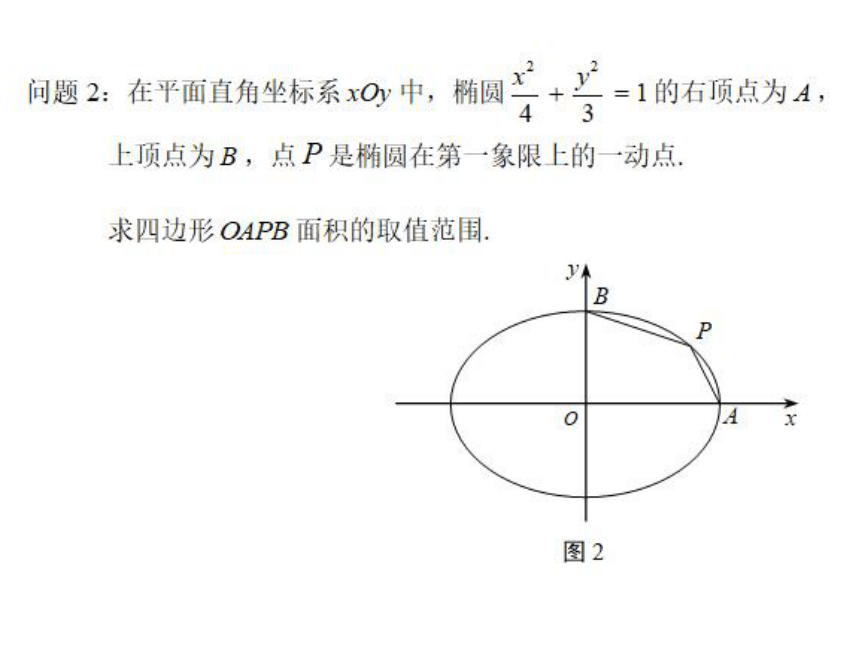
图2
问题2:在平面直角坐标系xOy中,椭圆x+2=1的右顶点为A,
上顶点为B,点P是椭圆在第一象限上的一动点
求四边形OAPB面积的取值范围
已知+题=1,x0>0,y>0,
43
求Z=130+10的范围
变式讲解2-1:在平面直角坐标系xOy中,椭圆+2=1的右顶点为A
上顶点为B,过原点O的直线与线段AB交于点D,与椭圆交于P,Q两点
求四边形APBQ面积的最大值
B
图2-1
1.在平面直角坐标系xy中,点P、Q为椭圆xy2=1上两动点,
且满足OP⊥OQ,求△OPQ面积的最值
图3
3.在平面直角坐标系xOy中,椭圆x+y=1的右顶点为A,
上顶点为B,过原点O的直线与线段AB交于点D,与椭圆交于
P,Q两点,设△APB的面积为S1,△AQB的面积为S2
求最大值
椭圆中与面积有关的
取值范围问题
解:法一:连结AB.
S四边形OAPB
=
S△OAB
+
S△PAB
转化为变式1?1
法二:连结OP,设P(x0,
y0).
S四边形OAPB
=
S△OPB
+
S△OPA
法三:过P作P
G
?
x轴于点G.
S四边形OAPB
=
S四边形OGPB
+
S△PGA
G
问题转化为:
法一(运用基本不等式):
法二:
法三:
线性规划(方程思想)
作业拓展
总结
借助几何图形,寻找存在“最值”的特殊位置;
2.建立面积的目标函数,用代数方法求此函数的最值;
(引入变元—建模—解模)
3.识图能力,运算能力,数据处理能力;
4.化归思想、数形结合思想;
5.通过一题多解,一题多变体会数学解题中的和谐统一之美.
品
田园高中团委学生会
图1
变式讲解1:在平面直角坐标系xOy中,点P为椭圆4+3=1上
动点,点Q的坐标为(3,).求△OPQ面积的最大值
Q
图1-1
变式讲解1:在平面直角坐标系xOy中,点P为椭圆x+=1上一动点,点Q的坐标为(3,y2)
4
求△OPQ面积的最大值
P
Q(3
解度P时第+,0+一
k=,直线0为和,昂y=0
=x-1l_△o-l
dp-ou++
45
图1-1
食十=第0代锅参),-08,和=130,0∈回可
十一08将8=40+),叶含∈,)
于
te[4So最大值为书
⊙线性划(推程鼠想),=%-士t
由{+4们=,际4)-=+x+已=04-4-6)=P(-+≥0
=X。-t
-4≤t≤4.
B
图2
问题2:在平面直角坐标系xOy中,椭圆x+2=1的右顶点为A,
上顶点为B,点P是椭圆在第一象限上的一动点
求四边形OAPB面积的取值范围
已知+题=1,x0>0,y>0,
43
求Z=130+10的范围
变式讲解2-1:在平面直角坐标系xOy中,椭圆+2=1的右顶点为A
上顶点为B,过原点O的直线与线段AB交于点D,与椭圆交于P,Q两点
求四边形APBQ面积的最大值
B
图2-1
1.在平面直角坐标系xy中,点P、Q为椭圆xy2=1上两动点,
且满足OP⊥OQ,求△OPQ面积的最值
图3
3.在平面直角坐标系xOy中,椭圆x+y=1的右顶点为A,
上顶点为B,过原点O的直线与线段AB交于点D,与椭圆交于
P,Q两点,设△APB的面积为S1,△AQB的面积为S2
求最大值
