沪教版高中数学高二下册第十一章11.2直线的倾斜角和斜率 课件 (共25张PPT)
文档属性
| 名称 | 沪教版高中数学高二下册第十一章11.2直线的倾斜角和斜率 课件 (共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 808.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-07 11:23:20 | ||
图片预览







文档简介
(共25张PPT)
倾斜角与斜率
直线的倾斜角与斜率
1.理解直线的斜率和倾斜角的概念;
2.理解直线倾斜角的惟一性及直线斜率的存在性;
3.了解斜率公式的推导过程,会应用斜率公式求直线的斜率.
问题导学
题型探究
达标检测
学习目标
问题导学
新知探究
点点落实
知识点一 直线的倾斜角
思考1 在平面直角坐标系中,只知道直线上的一点,能不能确定一条直1线呢?
答案 不能.
思考2 在平面直角坐标系中,过定点P的四条直线
如图所示,每条直线与x轴的相对倾斜程度是否相同?
答案 不同.
1.倾斜角的定义
(1)当直线l与x轴相交时,取x轴作为基准,x轴
与直线l向上方向之间所成的角α叫做直线l的倾斜角.
(2)当直线l与x轴平行或重合时,规定它的倾斜角为0°.
2.倾斜角的范围
直线的倾斜角α的取值范围为
.
3.确定平面直角坐标系中一条直线位置的几何要素是:直线上的一个
以及它的
.
正向
0°≤α<180°
定点
倾斜角
知识点二 直线的斜率与倾斜角的关系
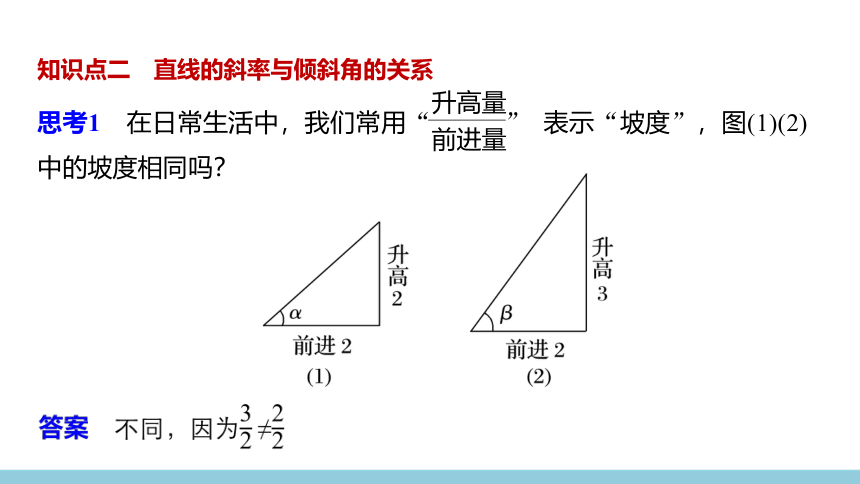
思考1 在日常生活中,我们常用“
”
表示“坡度”,图(1)(2)中的坡度相同吗?
前进量
升高量
?
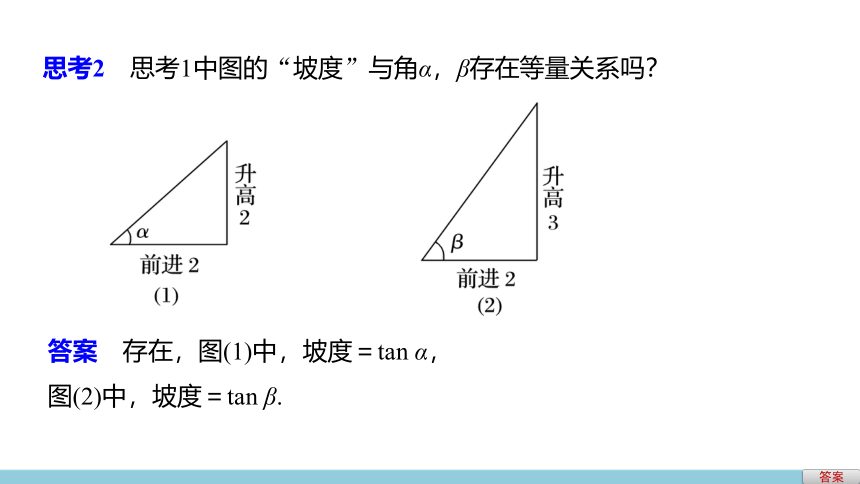
思考2 思考1中图的“坡度”与角α,β存在等量关系吗?
答案 存在,图(1)中,坡度=tan
α,
图(2)中,坡度=tan
β.
答案
1.直线的斜率
把一条直线的倾斜角α的
叫做这条直线的斜率,斜率常用小写字母k表示,即k=
.
2.斜率与倾斜角的对应关系
正切值
tan
α
图示
倾斜角(范围)
斜率(范围)
α=0°
k=0
0°<α<90°
k>0
α=90°
不存在
90°<α<180°
k<0
知识点三 过两点的直线的斜率公式
?
返回
?
答案
题型探究
重点难点
个个击破
类型一 直线的倾斜角
例1 设直线l过原点,其倾斜角为α,将直线l绕坐标原点沿逆时针方向旋转40°,得直线l1,则直线l1的倾斜角为( )
A.α+40°
B.α-140°
C.140°-α
D.当0°≤α<140°时为α+40°,当140°≤α<180°时为α-140°
解析
根据题意,画出图形,如图所示:
因为0°≤α<180°,显然A,B,C未分类讨论,均不全面,不合题意.
通过画图(如图所示)可知:
当0°≤α<140°时,l1的倾斜角为α+40°;
当140°≤α<180°时,l1的倾斜角为40°+α-180°=α-140°.故选D.
答案 D
反思与感悟
(1)解答本题要注意根据倾斜角的概念及倾斜角的取值范围解答.
(2)求直线的倾斜角主要根据定义来求,其关键是根据题意画出图形,找准倾斜角,有时要根据情况分类讨论.
跟踪训练1 已知直线l向上方向与y轴正向所成的角为30°,则直线l的倾斜角为___________.
解析
有两种情况:①如图(1),直线l向上方向与x轴正向所成的角为60°,即直线l的倾斜角为60°.
②如图(2),直线l向上方向与x轴正向所成的角为120°,即直线l的倾斜角为120°.
60°或120°
类型二 直线的斜率
例2
直线l1,l2,l3都经过点P(3,2),又l1,l2,l3分别经过点Q1(-2,-1),Q2(4,-2),Q3(-3,2),计算直线l1,l2,l3的斜率,并判断这些直线的倾斜角是锐角还是钝角.
?
反思与感悟
应用斜率公式时应先判定两定点的横坐标是否相等,若相等,直线垂直于x轴,斜率不存在;若不相等,再代入斜率公式求解.
跟踪训练2 (1)若经过A(m,3),B(1,2)两点的直线的倾斜角为45°,则m=
.
(2)经过A(m,3),B(1,2)两点的直线的倾斜角α的取值范围是_________
(其中m≥1).
2
0°<α≤90°
类型三 斜率与倾斜角的综合应用
例3、(1)已知某直线l的倾斜角为α=45
°,又P1(2,y1),
P2(x2,5),
P3(3,1)是此直线上的三点,求x2、y1的值
(2)已知A(3,3),B(-4,2),C(0,-2).若点D在线段BC上(包
括端点)移动,求直线AD的斜率的变化范围.
反思与感悟
(1)用斜率公式可解决三点共线问题
(2)斜率与倾斜角的关系如图:
跟踪训练3 (1)已知A(1,1),B(3,5),C(a,7),D(-1,b)四点在同一条直线上,求直线的斜率k及a,b的值.
?
(2)已知直线l过点P(1,1)且与线段MN相交,其中M(2,-3),N(-3,-2),求直线l的斜率k的取值范围.
解
如图所示,直线l绕着点P在直线PM与PN间旋转,l′是过P点且与x轴垂直的直线.
当l在PN位置转到l′位置时,
当l在l′位置转到PM位置时,
倾斜角大于90°,k≤kPM=-4.
1
2
3
达标检测
4
1.对于下列命题:
①若α是直线l的倾斜角,则0°≤α<180°;
②若k是直线的斜率,则k∈R;
③任一条直线都有倾斜角,但不一定有斜率;
④任一条直线都有斜率,但不一定有倾斜角.
其中正确命题的个数是( )
A.1
B.2
C.3
D.4
解析 ①②③正确.
C
1
2
3
4
2.m,n,p是两两不相等的实数,则点A(m+n,p),B(n+p,m),C(p+m,n)必( )
A.在同一条直线上
B.是直角三角形的顶点
C.是等腰三角形的顶点
D.是等边三角形的顶点
解析
∴A,B,C三点共线.
A
1
2
3
4
3.已知A(m,-m+3),B(2,m-1),C(-1,4),直线AC的斜率是直线BC的斜率的3倍,则m的值为____.
解析
由题意知,kAC=3kBC,
4
1
2
3
4
解析答案
4.求经过下列两点的直线的斜率,并判断其倾斜角是锐角还是钝角.
(1)(1,1),(2,4);
解
所以倾斜角是锐角;
所以倾斜角是钝角;
(2)(-3,5),(0,2);
解
1
2
3
4
(3)(2,3),(2,5);
(4)(3,-2),(6,-2).
解
由x1=x2=2得:k不存在,倾斜角是90°;
所以倾斜角为0°.
解
直线情况
平行于x轴
垂直于x轴
0
α的大小
0°
0°<α<90°
90°
90°<α<180°
k的范围
0
k>0
不存在
k<0
k的增减情况
?
k随α的增大而增大
?
k随α的增大而增大
学习小结
直线的斜率和倾斜角反映了直线的倾斜程度,二者紧密相连,如下表:
返回
倾斜角与斜率
直线的倾斜角与斜率
1.理解直线的斜率和倾斜角的概念;
2.理解直线倾斜角的惟一性及直线斜率的存在性;
3.了解斜率公式的推导过程,会应用斜率公式求直线的斜率.
问题导学
题型探究
达标检测
学习目标
问题导学
新知探究
点点落实
知识点一 直线的倾斜角
思考1 在平面直角坐标系中,只知道直线上的一点,能不能确定一条直1线呢?
答案 不能.
思考2 在平面直角坐标系中,过定点P的四条直线
如图所示,每条直线与x轴的相对倾斜程度是否相同?
答案 不同.
1.倾斜角的定义
(1)当直线l与x轴相交时,取x轴作为基准,x轴
与直线l向上方向之间所成的角α叫做直线l的倾斜角.
(2)当直线l与x轴平行或重合时,规定它的倾斜角为0°.
2.倾斜角的范围
直线的倾斜角α的取值范围为
.
3.确定平面直角坐标系中一条直线位置的几何要素是:直线上的一个
以及它的
.
正向
0°≤α<180°
定点
倾斜角
知识点二 直线的斜率与倾斜角的关系
思考1 在日常生活中,我们常用“
”
表示“坡度”,图(1)(2)中的坡度相同吗?
前进量
升高量
?
思考2 思考1中图的“坡度”与角α,β存在等量关系吗?
答案 存在,图(1)中,坡度=tan
α,
图(2)中,坡度=tan
β.
答案
1.直线的斜率
把一条直线的倾斜角α的
叫做这条直线的斜率,斜率常用小写字母k表示,即k=
.
2.斜率与倾斜角的对应关系
正切值
tan
α
图示
倾斜角(范围)
斜率(范围)
α=0°
k=0
0°<α<90°
k>0
α=90°
不存在
90°<α<180°
k<0
知识点三 过两点的直线的斜率公式
?
返回
?
答案
题型探究
重点难点
个个击破
类型一 直线的倾斜角
例1 设直线l过原点,其倾斜角为α,将直线l绕坐标原点沿逆时针方向旋转40°,得直线l1,则直线l1的倾斜角为( )
A.α+40°
B.α-140°
C.140°-α
D.当0°≤α<140°时为α+40°,当140°≤α<180°时为α-140°
解析
根据题意,画出图形,如图所示:
因为0°≤α<180°,显然A,B,C未分类讨论,均不全面,不合题意.
通过画图(如图所示)可知:
当0°≤α<140°时,l1的倾斜角为α+40°;
当140°≤α<180°时,l1的倾斜角为40°+α-180°=α-140°.故选D.
答案 D
反思与感悟
(1)解答本题要注意根据倾斜角的概念及倾斜角的取值范围解答.
(2)求直线的倾斜角主要根据定义来求,其关键是根据题意画出图形,找准倾斜角,有时要根据情况分类讨论.
跟踪训练1 已知直线l向上方向与y轴正向所成的角为30°,则直线l的倾斜角为___________.
解析
有两种情况:①如图(1),直线l向上方向与x轴正向所成的角为60°,即直线l的倾斜角为60°.
②如图(2),直线l向上方向与x轴正向所成的角为120°,即直线l的倾斜角为120°.
60°或120°
类型二 直线的斜率
例2
直线l1,l2,l3都经过点P(3,2),又l1,l2,l3分别经过点Q1(-2,-1),Q2(4,-2),Q3(-3,2),计算直线l1,l2,l3的斜率,并判断这些直线的倾斜角是锐角还是钝角.
?
反思与感悟
应用斜率公式时应先判定两定点的横坐标是否相等,若相等,直线垂直于x轴,斜率不存在;若不相等,再代入斜率公式求解.
跟踪训练2 (1)若经过A(m,3),B(1,2)两点的直线的倾斜角为45°,则m=
.
(2)经过A(m,3),B(1,2)两点的直线的倾斜角α的取值范围是_________
(其中m≥1).
2
0°<α≤90°
类型三 斜率与倾斜角的综合应用
例3、(1)已知某直线l的倾斜角为α=45
°,又P1(2,y1),
P2(x2,5),
P3(3,1)是此直线上的三点,求x2、y1的值
(2)已知A(3,3),B(-4,2),C(0,-2).若点D在线段BC上(包
括端点)移动,求直线AD的斜率的变化范围.
反思与感悟
(1)用斜率公式可解决三点共线问题
(2)斜率与倾斜角的关系如图:
跟踪训练3 (1)已知A(1,1),B(3,5),C(a,7),D(-1,b)四点在同一条直线上,求直线的斜率k及a,b的值.
?
(2)已知直线l过点P(1,1)且与线段MN相交,其中M(2,-3),N(-3,-2),求直线l的斜率k的取值范围.
解
如图所示,直线l绕着点P在直线PM与PN间旋转,l′是过P点且与x轴垂直的直线.
当l在PN位置转到l′位置时,
当l在l′位置转到PM位置时,
倾斜角大于90°,k≤kPM=-4.
1
2
3
达标检测
4
1.对于下列命题:
①若α是直线l的倾斜角,则0°≤α<180°;
②若k是直线的斜率,则k∈R;
③任一条直线都有倾斜角,但不一定有斜率;
④任一条直线都有斜率,但不一定有倾斜角.
其中正确命题的个数是( )
A.1
B.2
C.3
D.4
解析 ①②③正确.
C
1
2
3
4
2.m,n,p是两两不相等的实数,则点A(m+n,p),B(n+p,m),C(p+m,n)必( )
A.在同一条直线上
B.是直角三角形的顶点
C.是等腰三角形的顶点
D.是等边三角形的顶点
解析
∴A,B,C三点共线.
A
1
2
3
4
3.已知A(m,-m+3),B(2,m-1),C(-1,4),直线AC的斜率是直线BC的斜率的3倍,则m的值为____.
解析
由题意知,kAC=3kBC,
4
1
2
3
4
解析答案
4.求经过下列两点的直线的斜率,并判断其倾斜角是锐角还是钝角.
(1)(1,1),(2,4);
解
所以倾斜角是锐角;
所以倾斜角是钝角;
(2)(-3,5),(0,2);
解
1
2
3
4
(3)(2,3),(2,5);
(4)(3,-2),(6,-2).
解
由x1=x2=2得:k不存在,倾斜角是90°;
所以倾斜角为0°.
解
直线情况
平行于x轴
垂直于x轴
0
α的大小
0°
0°<α<90°
90°
90°<α<180°
k的范围
0
k>0
不存在
k<0
k的增减情况
?
k随α的增大而增大
?
k随α的增大而增大
学习小结
直线的斜率和倾斜角反映了直线的倾斜程度,二者紧密相连,如下表:
返回
