人教A版高中数学必修4第三章3.1.2两角和与差的正弦、余弦、正切公式课件(共20张PPT)
文档属性
| 名称 | 人教A版高中数学必修4第三章3.1.2两角和与差的正弦、余弦、正切公式课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 309.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-07 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
3.1.2两角和与差的
正弦、余弦、正切公式
1.复习
两角差的余弦公式
用-
?代替?看看有什么结果?
cos[?-(-?)]=
cos?cos(-?)+sin?sin(-?)
=
cos?cos?-sin?sin?
cos(?+?)
cos(?+?)
=
cos?cos?-sin?sin?
2.两个和的余弦公式
(
C(?+?)
)
思考:两角和与差的正弦公式是怎样的呢?
提示:利用诱导公式五(或六)可以实现正弦,余弦的互化
3.两角和的正弦公式
(S(?+?))
4.两角差的正弦公式
(S(?-?))
也可在S(?+?)用-
?代?得出
(
C(?-?)
)
(
C(?+?)
)
cos(?-?)=
cos?cos?+sin?sin?
cos(?+?)=
cos?cos?-sin?sin?
(
S(?+?)
)
(
S(?-?)
)
sin(?+?)=
sin?cos?+cos?sin?
sin(?-?)=
sin?cos?-cos?sin?
思考:两角和与差的正切公式是怎样的呢?
(这里有什么要求?)
(又有什么要求?)
6.两角差的正切公式
(T(?-?))
5.两角和的正切公式
(T(?+?))
那两角差的正切呢?
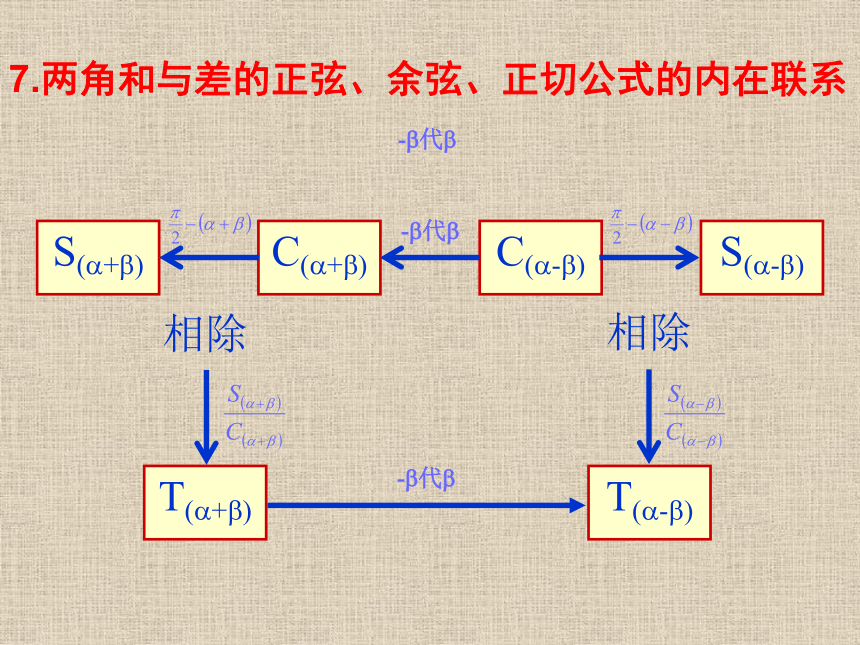
7.两角和与差的正弦、余弦、正切公式的内在联系
C(?-?)
8.例题讲解
例1
解:
?是第四象限角,得
例2
利用和(差)角公式计算下列各式的值
求下列各式的值
化简
构造角
10.小结
(
C(?-?)
)
(
C(?+?)
)
cos(?-?)=
cos?cos?+sin?sin?
cos(?+?)=
cos?cos?-sin?sin?
(
S(?+?)
)
(
S(?-?)
)
sin(?+?)=
sin?cos?+cos?sin?
sin(?-?)=
sin?cos?-cos?sin?
(
T(?+?)
)
(
T(?-?)
)
两角和与差的正弦、余弦、正切公式
同名积,符号反。
异名积,符号同。
+
+
余弦:
同名积
符号反
正切:
符号上同
下不同
正弦:
异名积
符号同
3.1.2两角和与差的
正弦、余弦、正切公式
1.复习
两角差的余弦公式
用-
?代替?看看有什么结果?
cos[?-(-?)]=
cos?cos(-?)+sin?sin(-?)
=
cos?cos?-sin?sin?
cos(?+?)
cos(?+?)
=
cos?cos?-sin?sin?
2.两个和的余弦公式
(
C(?+?)
)
思考:两角和与差的正弦公式是怎样的呢?
提示:利用诱导公式五(或六)可以实现正弦,余弦的互化
3.两角和的正弦公式
(S(?+?))
4.两角差的正弦公式
(S(?-?))
也可在S(?+?)用-
?代?得出
(
C(?-?)
)
(
C(?+?)
)
cos(?-?)=
cos?cos?+sin?sin?
cos(?+?)=
cos?cos?-sin?sin?
(
S(?+?)
)
(
S(?-?)
)
sin(?+?)=
sin?cos?+cos?sin?
sin(?-?)=
sin?cos?-cos?sin?
思考:两角和与差的正切公式是怎样的呢?
(这里有什么要求?)
(又有什么要求?)
6.两角差的正切公式
(T(?-?))
5.两角和的正切公式
(T(?+?))
那两角差的正切呢?
7.两角和与差的正弦、余弦、正切公式的内在联系
C(?-?)
8.例题讲解
例1
解:
?是第四象限角,得
例2
利用和(差)角公式计算下列各式的值
求下列各式的值
化简
构造角
10.小结
(
C(?-?)
)
(
C(?+?)
)
cos(?-?)=
cos?cos?+sin?sin?
cos(?+?)=
cos?cos?-sin?sin?
(
S(?+?)
)
(
S(?-?)
)
sin(?+?)=
sin?cos?+cos?sin?
sin(?-?)=
sin?cos?-cos?sin?
(
T(?+?)
)
(
T(?-?)
)
两角和与差的正弦、余弦、正切公式
同名积,符号反。
异名积,符号同。
+
+
余弦:
同名积
符号反
正切:
符号上同
下不同
正弦:
异名积
符号同
