人教A版数学必修4第一章1.4.3 正切函数的性质和图象教案
文档属性
| 名称 | 人教A版数学必修4第一章1.4.3 正切函数的性质和图象教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 254.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-07 00:00:00 | ||
图片预览


文档简介
§1.4.3
正切函数的图像与性质
教材分析
《正切函数的图象和性质》
它前承正、余弦函数,后启必修五中的直线斜率问题。研究正切函数的图象与性质过程不仅是对正、余弦曲线研讨方法的一种再现,更是一种提升,同时又为后续的学习奠定了基石。教材的安排是先研究正切函数的性质,再根据性质来画出图像。但是我对这节课进行了调整,先由正切线和正切函数部分性质来画出图像,再更加直观的研究正切函数的其他性质。正弦函数在研究方法上类似,我采用以类比的方式,让学生回忆正弦曲线的作图过程与方法,进而启发、引导学生发现作正切曲线的一种方法。教材上直接圈定了区间(),这样限制了学生的思维,我把问题留给学生思考,采用让学生自己选择周期,并比较得出最优区间,激发学生的思考能力。
教学目标
知识与技能
体会类比方法在画正切函数图像发挥的作用,会画正切函数的草图。通过图像观察性质,培养观察分析、归纳总结的能力。在对性质进行归纳总结后,还要能对性质进行简单的应用。
过程与方法
引导学生分析正切函数的周期性和在()的奇偶性,简化用正切线画正切函数图像的方法,让学生学会思考从本身函数性质入手简化问题,再反过来由图像归纳其性质的研究方法。
3.
情感态度与价值观
在画图像过程中,感受其对称美。
三、教学重点与难点
1.
教学重点
画正切函数的图像,归纳其性质,会简单应用性质。
教学难点
分析并用正切线画出正切函数的图像。
教学流程设计
复习引入
如何用正弦线作正弦函数图像的呢?引导学生用同样的方法作正切函数图像。
探究用正切线作正切函数图像
师生活动:回顾:正切线的作法
师生活动:分析:正切函数是否为周期函数?
(教师作适当引导,得出正切函数的最小正周期为,大部分学生会认为是)
学生活动:思考问题:先作正切函数哪个区间上的图像呢?
(可以是吗?(图像会间断)引发学生思考)
[设计意图]
引导学生用类比的思维方法得到先画出正切函数一个周期内的图像,并放手让学生自己去选择区间,从而自然地解释选择的最优区间为。
从解析式的角度看,正切函数在区间上奇偶性如何?
[设计意图]
进一步利用性质将图像区间简化为,利用对称性画出左半部分图像。
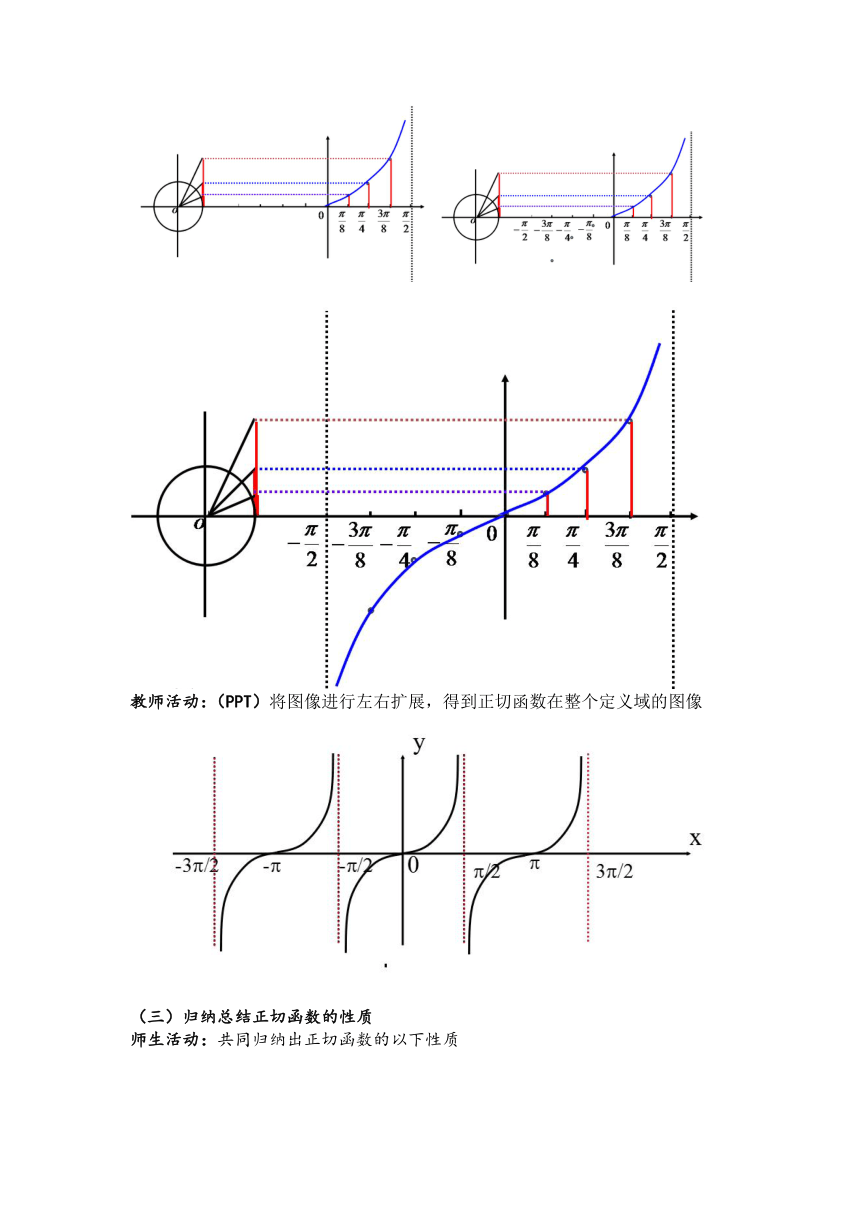
教师活动:(PPT展示)作,的图象
作法:1、把单位圆第一象限圆分成4等分
2、作正切线
3、平移(强调在时正切函数没有意义,因此画一条虚线表示虚线上的任意点都不可能落在虚线上,并且教师引导学生观察在,正切线的大小变化,从而得出整体函数图像呈现上升的趋势,并无限靠近虚线)
4、连线
5、对称性完成选定区间上的图像
教师活动:(PPT)将图像进行左右扩展,得到正切函数在整个定义域的图像
归纳总结正切函数的性质
师生活动:共同归纳出正切函数的以下性质
(此性质板书)
学生活动:思考问题:正切函数是定义域上的增函数吗?
[设计意图]
再次强调是在每一个开区间上是增函数。
例题讲解
例1
不用计算器,比较下列每组数的大小
(1)
与
(2)与
例2
求函数的定义域、周期和单调区间.
反馈演练
求函数定义域、值域、单调区间、奇偶性和周期性。(作为作业)
小结
正切曲线的画法
函数的主要性质
板书设计
(
§
1.4.3
正切函数的图像与性质
函数
定义域
值域
R
周期性
奇偶性
奇
单调性
增区间
)
(
例题演示
(例
1
演示完擦掉,再演示例
2
)
)
正切函数的图像与性质
教材分析
《正切函数的图象和性质》
它前承正、余弦函数,后启必修五中的直线斜率问题。研究正切函数的图象与性质过程不仅是对正、余弦曲线研讨方法的一种再现,更是一种提升,同时又为后续的学习奠定了基石。教材的安排是先研究正切函数的性质,再根据性质来画出图像。但是我对这节课进行了调整,先由正切线和正切函数部分性质来画出图像,再更加直观的研究正切函数的其他性质。正弦函数在研究方法上类似,我采用以类比的方式,让学生回忆正弦曲线的作图过程与方法,进而启发、引导学生发现作正切曲线的一种方法。教材上直接圈定了区间(),这样限制了学生的思维,我把问题留给学生思考,采用让学生自己选择周期,并比较得出最优区间,激发学生的思考能力。
教学目标
知识与技能
体会类比方法在画正切函数图像发挥的作用,会画正切函数的草图。通过图像观察性质,培养观察分析、归纳总结的能力。在对性质进行归纳总结后,还要能对性质进行简单的应用。
过程与方法
引导学生分析正切函数的周期性和在()的奇偶性,简化用正切线画正切函数图像的方法,让学生学会思考从本身函数性质入手简化问题,再反过来由图像归纳其性质的研究方法。
3.
情感态度与价值观
在画图像过程中,感受其对称美。
三、教学重点与难点
1.
教学重点
画正切函数的图像,归纳其性质,会简单应用性质。
教学难点
分析并用正切线画出正切函数的图像。
教学流程设计
复习引入
如何用正弦线作正弦函数图像的呢?引导学生用同样的方法作正切函数图像。
探究用正切线作正切函数图像
师生活动:回顾:正切线的作法
师生活动:分析:正切函数是否为周期函数?
(教师作适当引导,得出正切函数的最小正周期为,大部分学生会认为是)
学生活动:思考问题:先作正切函数哪个区间上的图像呢?
(可以是吗?(图像会间断)引发学生思考)
[设计意图]
引导学生用类比的思维方法得到先画出正切函数一个周期内的图像,并放手让学生自己去选择区间,从而自然地解释选择的最优区间为。
从解析式的角度看,正切函数在区间上奇偶性如何?
[设计意图]
进一步利用性质将图像区间简化为,利用对称性画出左半部分图像。
教师活动:(PPT展示)作,的图象
作法:1、把单位圆第一象限圆分成4等分
2、作正切线
3、平移(强调在时正切函数没有意义,因此画一条虚线表示虚线上的任意点都不可能落在虚线上,并且教师引导学生观察在,正切线的大小变化,从而得出整体函数图像呈现上升的趋势,并无限靠近虚线)
4、连线
5、对称性完成选定区间上的图像
教师活动:(PPT)将图像进行左右扩展,得到正切函数在整个定义域的图像
归纳总结正切函数的性质
师生活动:共同归纳出正切函数的以下性质
(此性质板书)
学生活动:思考问题:正切函数是定义域上的增函数吗?
[设计意图]
再次强调是在每一个开区间上是增函数。
例题讲解
例1
不用计算器,比较下列每组数的大小
(1)
与
(2)与
例2
求函数的定义域、周期和单调区间.
反馈演练
求函数定义域、值域、单调区间、奇偶性和周期性。(作为作业)
小结
正切曲线的画法
函数的主要性质
板书设计
(
§
1.4.3
正切函数的图像与性质
函数
定义域
值域
R
周期性
奇偶性
奇
单调性
增区间
)
(
例题演示
(例
1
演示完擦掉,再演示例
2
)
)
