人教A版数学必修4第一章1.4.3 正切函数的性质和图象课件(共23张PPT)
文档属性
| 名称 | 人教A版数学必修4第一章1.4.3 正切函数的性质和图象课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-07 11:45:39 | ||
图片预览





文档简介
(共23张PPT)
探究:你能否根据研究正弦、余弦函数的图象和性质的经验以同样的方法研究正切函数的图像和性质?
§1.4.3正切函数的性质与图像
1、利用正切函数的定义,写出正切函数的定义域;
由诱导公式知
§1.4.3正切函数的性质与图像
由诱导公式知
§1.4.3正切函数的性质与图像
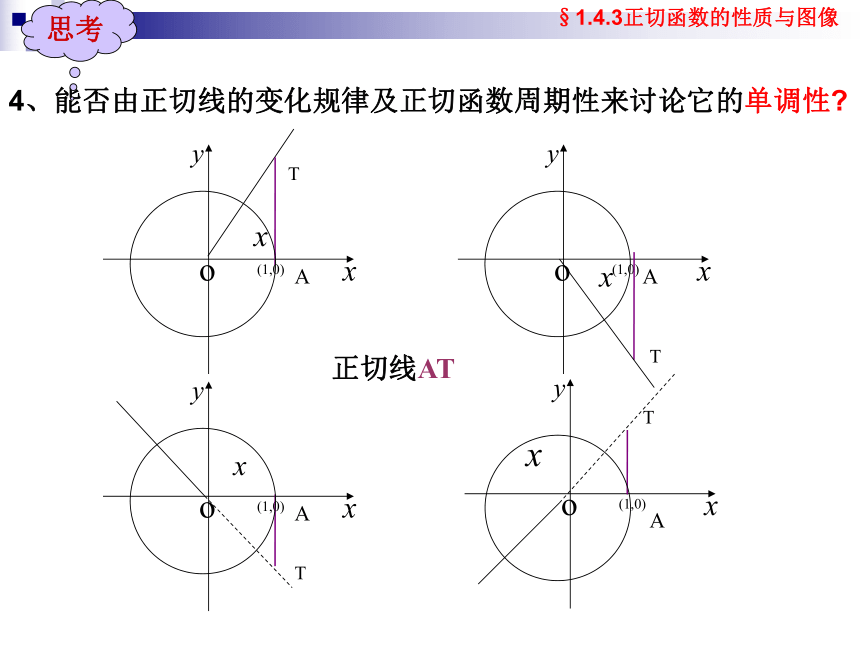
4、能否由正切线的变化规律及正切函数周期性来讨论它的单调性?
§1.4.3正切函数的性质与图像
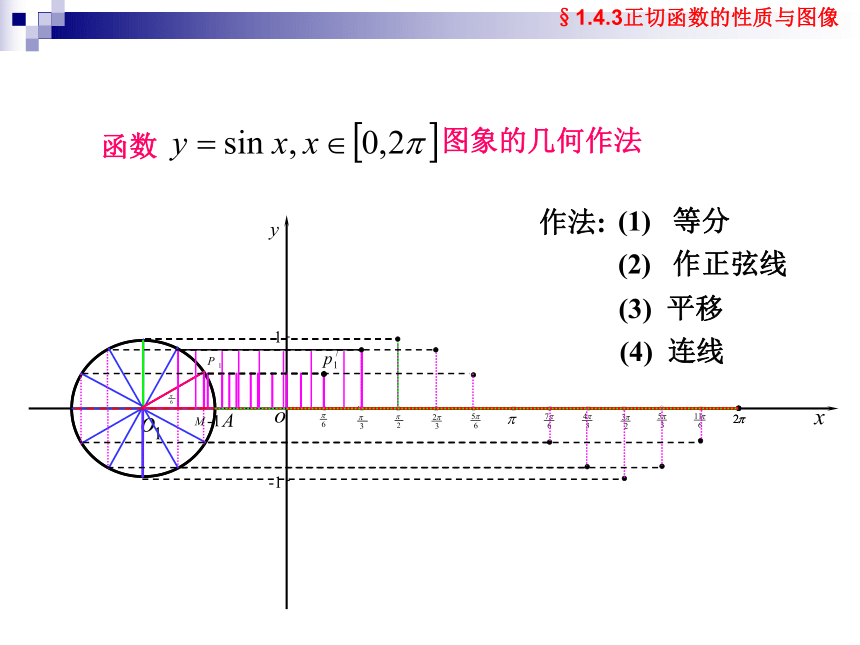
作法:
(1)
等分
(2)
作正弦线
(3)
平移
(4)
连线
§1.4.3正切函数的性质与图像
4、能否由正切线的变化规律及正切函数周期性来讨论它的单调性?
思考
A
T
正切线AT
A
T
A
T
A
T
§1.4.3正切函数的性质与图像
§1.4.3正切函数的性质与图像
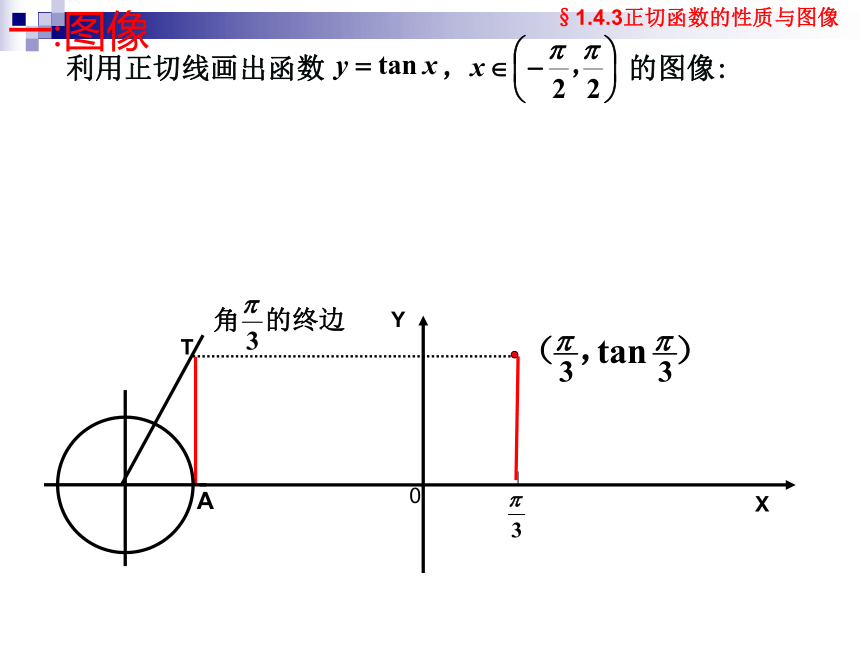
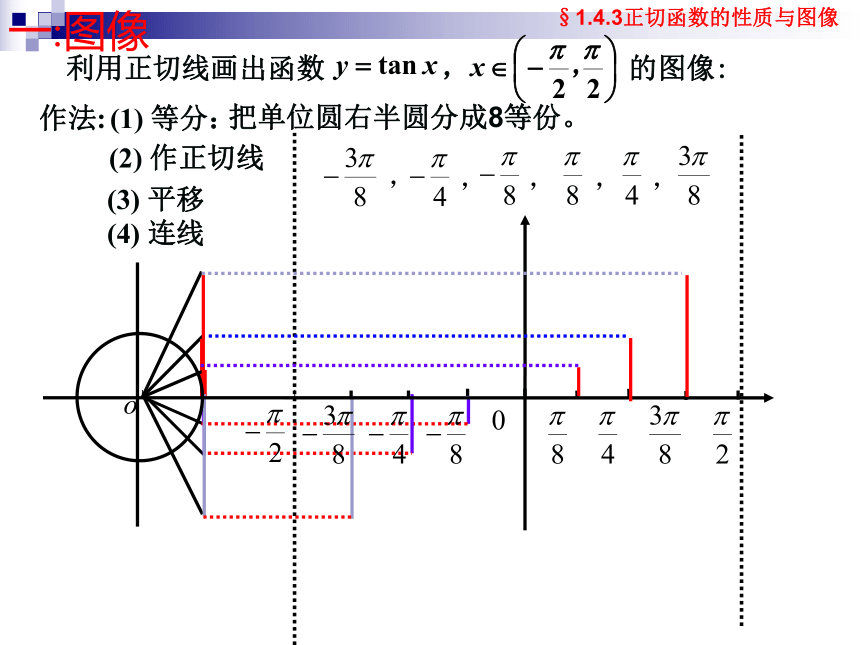
一:图像
作法:
(1)
等分:
(2)
作正切线
(3)
平移
(4)
连线
把单位圆右半圆分成8等份。
§1.4.3正切函数的性质与图像
一:图像
y
x
1
-1
?
-?
0
定义域
值域
周期性
奇偶性
单调性
R
T=
?
奇函数
函数
y=tanx
二:性质
t
t+?
t-?
你能从正切函数的图象出发,讨论它的性质吗?
§1.4.3正切函数的性质与图像
(1)正切函数是整个定义域上的增函数吗?为什么?
(2)正切函数会不会在某一区间内是减函数?为什么?
讨论:
§1.4.3正切函数的性质与图像
A
是奇函数
B
在整个定义域上是增函数
C
在定义域内无最大值和最小值
D
平行于
轴的的直线被正切曲线各支所截线段相等
1.关于正切函数
,
下列判断不正确的是(
)
2.函数 的一个对称中心是( )
A
.
B.
C.
D.
基础练习
B
C
§1.4.3正切函数的性质与图像
例题分析
例1、求函数y=
的定义域、周期和单调区间
§1.4.3正切函数的性质与图像
例题分析
练习、求函数y=
的定义域、周期和单调区间
§1.4.3正切函数的性质与图像
例2、比较下列每组数的大小。
说明:比较两个正切值大小,关键是把相应的角
化到y=tanx的同一单调区间内,再利用y=tanx的单调递增性解决。
§1.4.3正切函数的性质与图像
例题分析
解:
§1.4.3正切函数的性质与图像
例题分析
[题组1]
1、求函数y=tan3x的定义域,值域,单调增区间
反馈演练
§1.4.3正切函数的性质与图像
<
>
反馈演练
§1.4.3正切函数的性质与图像
2、比较大小
答案:
(1)
(
2)
§1.4.3正切函数的性质与图像
反馈演练
[题组2]
1、求函数
的定义域、单调性、对称中心
提高练习
答案:
§1.4.3正切函数的性质与图像
2、单调性
3、对称中心
[题组2]
提高练习
[题组2]
2、
y
x
1
-1
?
-?
0
定义域
值域
周期性
奇偶性
单调性
R
T=
?
奇函数
函数
y=tanx
t
t+?
t-?
§1.4.3正切函数的性质与图像
总结:
正切函数的图象与性质
探究:你能否根据研究正弦、余弦函数的图象和性质的经验以同样的方法研究正切函数的图像和性质?
§1.4.3正切函数的性质与图像
1、利用正切函数的定义,写出正切函数的定义域;
由诱导公式知
§1.4.3正切函数的性质与图像
由诱导公式知
§1.4.3正切函数的性质与图像
4、能否由正切线的变化规律及正切函数周期性来讨论它的单调性?
§1.4.3正切函数的性质与图像
作法:
(1)
等分
(2)
作正弦线
(3)
平移
(4)
连线
§1.4.3正切函数的性质与图像
4、能否由正切线的变化规律及正切函数周期性来讨论它的单调性?
思考
A
T
正切线AT
A
T
A
T
A
T
§1.4.3正切函数的性质与图像
§1.4.3正切函数的性质与图像
一:图像
作法:
(1)
等分:
(2)
作正切线
(3)
平移
(4)
连线
把单位圆右半圆分成8等份。
§1.4.3正切函数的性质与图像
一:图像
y
x
1
-1
?
-?
0
定义域
值域
周期性
奇偶性
单调性
R
T=
?
奇函数
函数
y=tanx
二:性质
t
t+?
t-?
你能从正切函数的图象出发,讨论它的性质吗?
§1.4.3正切函数的性质与图像
(1)正切函数是整个定义域上的增函数吗?为什么?
(2)正切函数会不会在某一区间内是减函数?为什么?
讨论:
§1.4.3正切函数的性质与图像
A
是奇函数
B
在整个定义域上是增函数
C
在定义域内无最大值和最小值
D
平行于
轴的的直线被正切曲线各支所截线段相等
1.关于正切函数
,
下列判断不正确的是(
)
2.函数 的一个对称中心是( )
A
.
B.
C.
D.
基础练习
B
C
§1.4.3正切函数的性质与图像
例题分析
例1、求函数y=
的定义域、周期和单调区间
§1.4.3正切函数的性质与图像
例题分析
练习、求函数y=
的定义域、周期和单调区间
§1.4.3正切函数的性质与图像
例2、比较下列每组数的大小。
说明:比较两个正切值大小,关键是把相应的角
化到y=tanx的同一单调区间内,再利用y=tanx的单调递增性解决。
§1.4.3正切函数的性质与图像
例题分析
解:
§1.4.3正切函数的性质与图像
例题分析
[题组1]
1、求函数y=tan3x的定义域,值域,单调增区间
反馈演练
§1.4.3正切函数的性质与图像
<
>
反馈演练
§1.4.3正切函数的性质与图像
2、比较大小
答案:
(1)
(
2)
§1.4.3正切函数的性质与图像
反馈演练
[题组2]
1、求函数
的定义域、单调性、对称中心
提高练习
答案:
§1.4.3正切函数的性质与图像
2、单调性
3、对称中心
[题组2]
提高练习
[题组2]
2、
y
x
1
-1
?
-?
0
定义域
值域
周期性
奇偶性
单调性
R
T=
?
奇函数
函数
y=tanx
t
t+?
t-?
§1.4.3正切函数的性质与图像
总结:
正切函数的图象与性质
