人教版数学必修四第一章1.4.1 正弦函数、余弦函数的图象 配套教学课件(共22张PPT)
文档属性
| 名称 | 人教版数学必修四第一章1.4.1 正弦函数、余弦函数的图象 配套教学课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-07 16:35:33 | ||
图片预览





文档简介
(共22张PPT)
函数
函数
函数
函数
正弦函数、余弦函数的图象
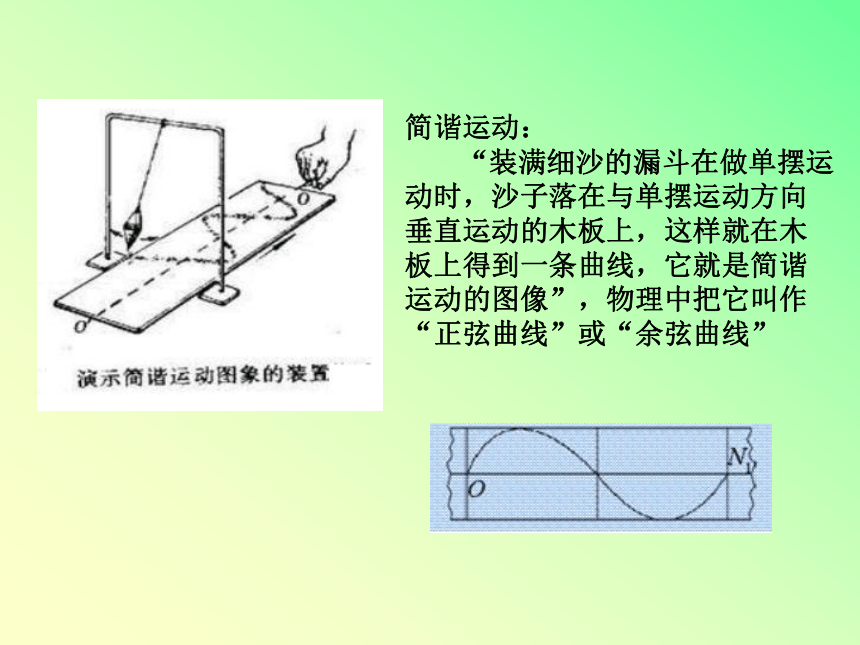
简谐运动:
“装满细沙的漏斗在做单摆运动时,沙子落在与单摆运动方向垂直运动的木板上,这样就在木板上得到一条曲线,它就是简谐运动的图像”,物理中把它叫作“正弦曲线”或“余弦曲线”
一、正弦函数、余弦函数的定义
给定一个实数x,有唯一确定的值sinx(或cosx)与之对应,由这个对应法则所确定的函数y=sinx(或y=cosx)叫做正弦函数(或余弦函数)
(1)
列表
(2)
描点
(3)
连线
用代数描点法作正弦函数的图象
P
M
A
T
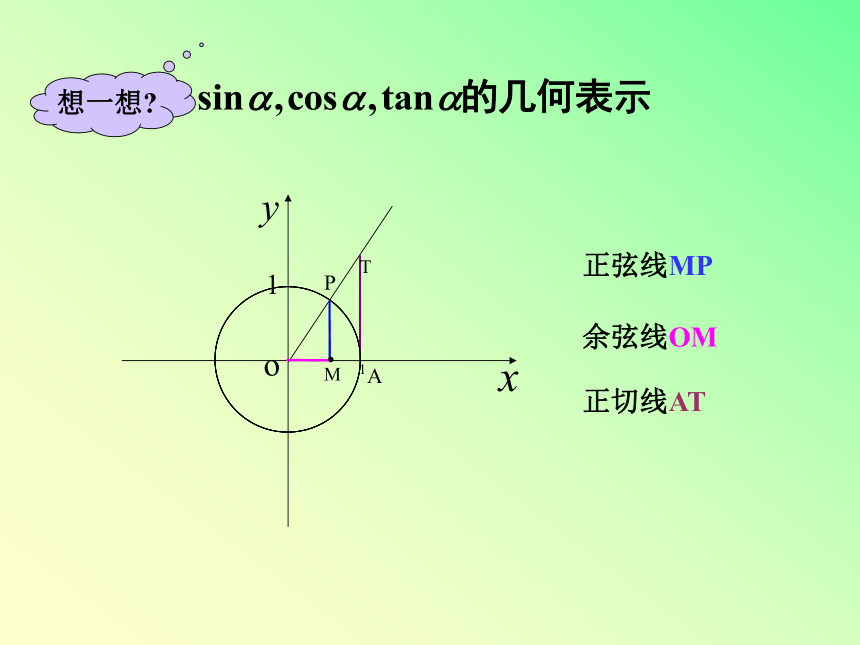
正弦线MP
余弦线OM
正切线AT
想一想?
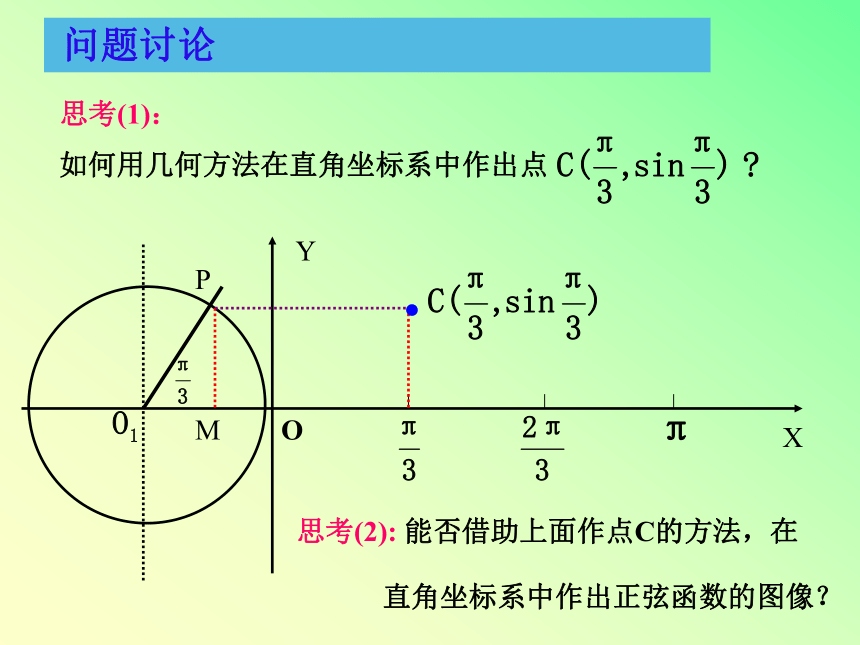
思考(1):
如何用几何方法在直角坐标系中作出点
O
P
M
X
Y
.
问题讨论
思考(2):
能否借助上面作点C的方法,在
直角坐标系中作出正弦函数的图像?
2、用几何描点法作正弦函数的图象
o1
x
y
o
-1
1
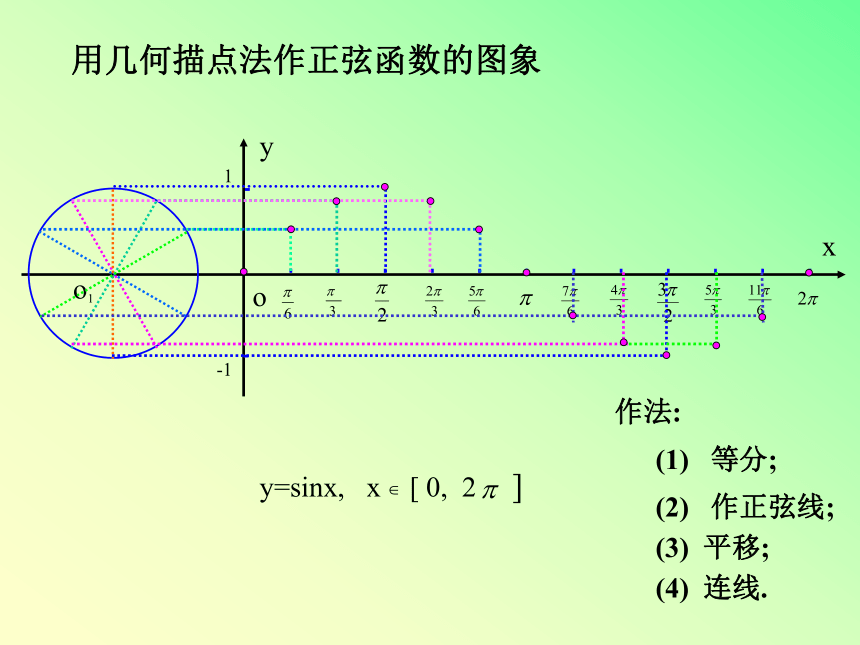
作法:
(1)
等分;
(2)
作正弦线;
(3)
平移;
作法:
(1)
等分;
2、用几何描点法作正弦函数的图象
(4)
连线.
(2)
作正弦线;
(3)
平移;
作法:
(1)
等分;
用几何描点法作正弦函数的图象
y=sinx
x?[0,2?]
y=sinx
x?R
终边相同角的三角函数值相等
即:
sin(x+2k?)=sinx,
k?Z
利用图象平移
正弦曲线
与
x
轴的交点:
图象的最高点:
图象的最低点:
观察
y
=
sin
x
,x?[
0,2
?]
图象的最高点、最低点和图象与
x
轴的交点坐标分别是什么?
五点
作图法
列表:列出对图象形状起关键作用的五点坐标.
连线:用光滑的曲线顺次连结五个点.
描点:定出五个关键点.
3、用五点法作正弦函数的图象
归纳小结
1.代数描点法(误差大)
2.几何描点法(精确但步骤繁)
3.五点法(重点掌握)
其中五点法最常用,要牢记五个关键点的坐标。
正弦曲线
的作法
你能以正弦函数的图像为基础,通过适当的图形变换得到余弦函数的图像吗?
想一想?
由诱导公式六
函数y=cosx,x∈[0,2π]的图象如何?其中起关键作用的点有哪几个?
思考:若用列表描点画y=cosx,x?[0,2?]
的草图,抓哪些关键的点?
1、画出下列函数的简图
(1)y=sinx+1,
x∈[0,2π]
列表
描点作图
(2)y=-cosx
,
x∈[0,2π]
1
0
-1
0
1
-1
0
1
0
-1
x
y=sinx
y=sin(-x)
用五点法画出y=sin(-x)
x∈[0,2π]的图像
0
x
y
2?
-2?
?
-?
1
-1
正弦曲线、余弦曲线的作法
1.代数描点法(误差大)
2.几何描点法(精确但步骤繁)
3.五点法(重点掌握)
4.图像变换
作业:
y=1-sinx
x∈[0,2π]
y=3cosx
x∈[0,2π]
y=
sinx
x∈[0,2π]
1.
画出下列函数的简图
函数
函数
函数
函数
正弦函数、余弦函数的图象
简谐运动:
“装满细沙的漏斗在做单摆运动时,沙子落在与单摆运动方向垂直运动的木板上,这样就在木板上得到一条曲线,它就是简谐运动的图像”,物理中把它叫作“正弦曲线”或“余弦曲线”
一、正弦函数、余弦函数的定义
给定一个实数x,有唯一确定的值sinx(或cosx)与之对应,由这个对应法则所确定的函数y=sinx(或y=cosx)叫做正弦函数(或余弦函数)
(1)
列表
(2)
描点
(3)
连线
用代数描点法作正弦函数的图象
P
M
A
T
正弦线MP
余弦线OM
正切线AT
想一想?
思考(1):
如何用几何方法在直角坐标系中作出点
O
P
M
X
Y
.
问题讨论
思考(2):
能否借助上面作点C的方法,在
直角坐标系中作出正弦函数的图像?
2、用几何描点法作正弦函数的图象
o1
x
y
o
-1
1
作法:
(1)
等分;
(2)
作正弦线;
(3)
平移;
作法:
(1)
等分;
2、用几何描点法作正弦函数的图象
(4)
连线.
(2)
作正弦线;
(3)
平移;
作法:
(1)
等分;
用几何描点法作正弦函数的图象
y=sinx
x?[0,2?]
y=sinx
x?R
终边相同角的三角函数值相等
即:
sin(x+2k?)=sinx,
k?Z
利用图象平移
正弦曲线
与
x
轴的交点:
图象的最高点:
图象的最低点:
观察
y
=
sin
x
,x?[
0,2
?]
图象的最高点、最低点和图象与
x
轴的交点坐标分别是什么?
五点
作图法
列表:列出对图象形状起关键作用的五点坐标.
连线:用光滑的曲线顺次连结五个点.
描点:定出五个关键点.
3、用五点法作正弦函数的图象
归纳小结
1.代数描点法(误差大)
2.几何描点法(精确但步骤繁)
3.五点法(重点掌握)
其中五点法最常用,要牢记五个关键点的坐标。
正弦曲线
的作法
你能以正弦函数的图像为基础,通过适当的图形变换得到余弦函数的图像吗?
想一想?
由诱导公式六
函数y=cosx,x∈[0,2π]的图象如何?其中起关键作用的点有哪几个?
思考:若用列表描点画y=cosx,x?[0,2?]
的草图,抓哪些关键的点?
1、画出下列函数的简图
(1)y=sinx+1,
x∈[0,2π]
列表
描点作图
(2)y=-cosx
,
x∈[0,2π]
1
0
-1
0
1
-1
0
1
0
-1
x
y=sinx
y=sin(-x)
用五点法画出y=sin(-x)
x∈[0,2π]的图像
0
x
y
2?
-2?
?
-?
1
-1
正弦曲线、余弦曲线的作法
1.代数描点法(误差大)
2.几何描点法(精确但步骤繁)
3.五点法(重点掌握)
4.图像变换
作业:
y=1-sinx
x∈[0,2π]
y=3cosx
x∈[0,2π]
y=
sinx
x∈[0,2π]
1.
画出下列函数的简图
