人教版数学必修四第一章1.4.3 正切函数的性质和图象 导学案(无答案)
文档属性
| 名称 | 人教版数学必修四第一章1.4.3 正切函数的性质和图象 导学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 134.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-07 00:00:00 | ||
图片预览

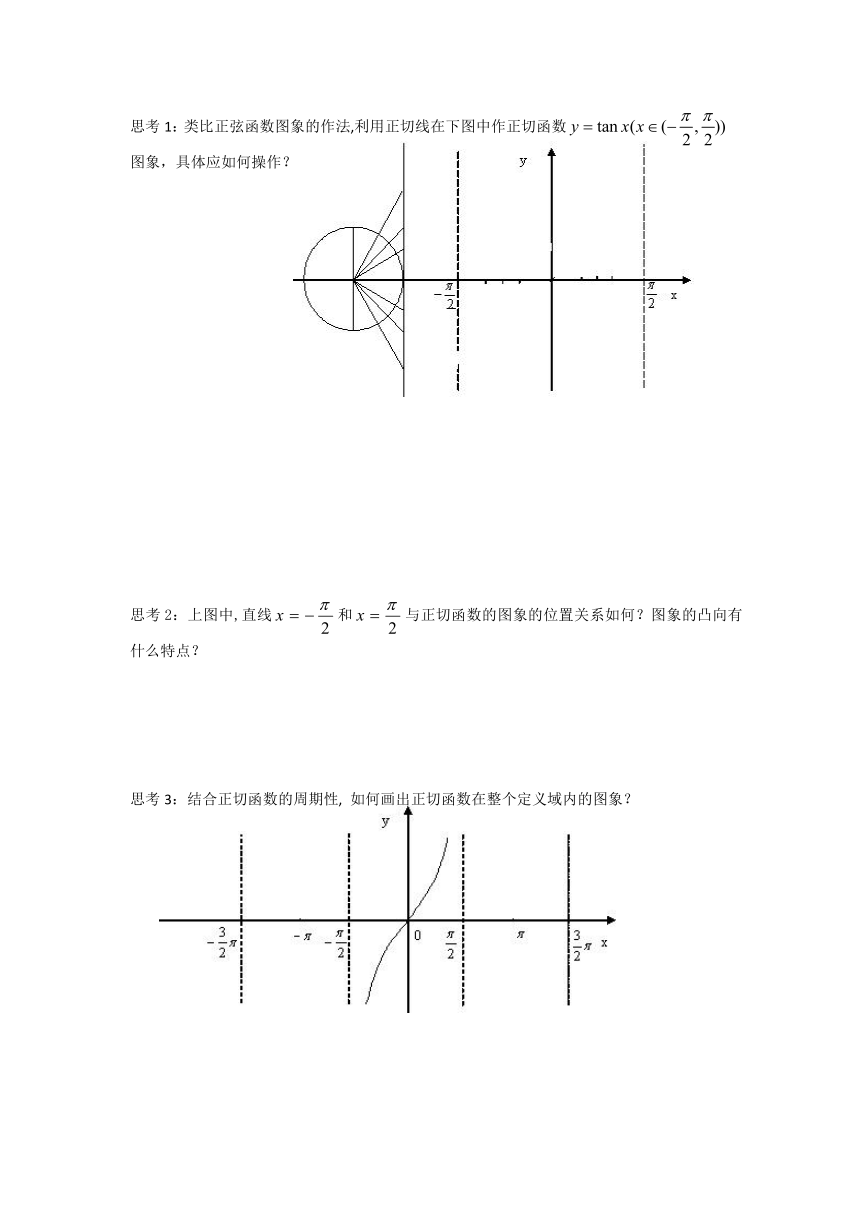


文档简介
1.4.3正切函数的图像与性质
【学习目标】
1、能正确作出正切函数图像;
2、借助图像理解正切函数的性质;
3、进一步研究正切函数的综合运用.
【重点难点】
正切函数的图像与性质
【学习过程】
一、复习旧知
1.画出下列各角的正切线:
2.正、余弦函数的图象是通过什么方法作出的?
3.正、余弦函数的基本性质包括哪些内容?
二、自主学习
预习教材P42~
P45思考以下问题:
知识探究(一):正切函数的图象
思考1:类比正弦函数图象的作法,利用正切线在下图中作正切函数图象,具体应如何操作?
思考2:上图中,直线和与正切函数的图象的位置关系如何?图象的凸向有什么特点?
思考3:结合正切函数的周期性,
如何画出正切函数在整个定义域内的图象?
思考4:正切函数的图象叫做正切曲线.它是由被相互平行的直线所隔开的无穷多支完成相同的曲线组成的。因为正切函数是奇函数,所以正切曲线关于原点对称,此外,正切曲线是否还关于其它的点和直线对称?
知识探究(二):正切函数的性质
观察正切函数的图象,完成下列思考:
思考1:正切函数的定义域是
,
用区间表示为
思考2:根据诱导公式与周期函数的定义结合正切函数的图象,你能判断正切函数是周期函数吗?其最小正周期是什么??
思考3:根据图像你能判断正切函数具有奇偶性吗?
思考4:观察右图中的正切线,当角x在内增加时,
正切函数值发生什么变化?由此反映出一个什么性质?
思考5:结合正切函数的周期性,正切函数的单调性如何?
思考6:正切函数在整个定义域内是增函数吗?正切函数会不会在某一区间内是减函数?
思考7:正切函数的值域是什么?
三、典型例题
例1:比较下列两个三角函数值的大小.
(1)
(2)
变式练习1:比较下列两个三角函数值的大小.
(1)
(2)
例2:根据正切函数图象,分别写出满足下列条件的的集合:
(1)
(2)
(3)
变式练习2:(1)函数的定义域是
(2)函数的定义域是
例3:研究函数的基本性质
变式训练3:(1)求函数的基本性质
(2)求函数的定义域、周期和单调区间.
课后思考:研究函数的相关性质
课后练习与提高
1.
下列函数不等式中正确的是(
).
A.
B.
C.
D.
2.
若,则(
).
A.
B.
C.
D.
3.
函数的定义域为(
).
A.
B.
D.且
4.
函数的周期是
(
)
A.
B.
C.
D.
5.
函数的最小正周期是(
)
A.
B.
C.
D.
6.
函数的周期为(
).
A.
B.
C.
D.
7.
直线(a为常数)与正切曲线为常数,且相交的两相邻点间的距离为(
).
A.
B.
C.
D.与a值有关
8.
函数的定义域是(
)
A.
{且}
B.
{且}
C.
{且}
D.
{且}
9.
在下列函数中,同时满足:①在上递增;②以为周期;③是奇函数的是(
).
A.
B.
C.
D.
10.
的大小关系是
.
11.
函数的定义域为
.
12.
函数与的图像在上有
个交点。
13.
函数y=tan(的值域是
14.
求函数的定义域、值域,并指出它的奇偶性、单调性以及周期.
判断函数的奇偶性
16.
已知,求的最小值。
17.
已知(|x|≤)的最小值-4,求a的值.
【学习目标】
1、能正确作出正切函数图像;
2、借助图像理解正切函数的性质;
3、进一步研究正切函数的综合运用.
【重点难点】
正切函数的图像与性质
【学习过程】
一、复习旧知
1.画出下列各角的正切线:
2.正、余弦函数的图象是通过什么方法作出的?
3.正、余弦函数的基本性质包括哪些内容?
二、自主学习
预习教材P42~
P45思考以下问题:
知识探究(一):正切函数的图象
思考1:类比正弦函数图象的作法,利用正切线在下图中作正切函数图象,具体应如何操作?
思考2:上图中,直线和与正切函数的图象的位置关系如何?图象的凸向有什么特点?
思考3:结合正切函数的周期性,
如何画出正切函数在整个定义域内的图象?
思考4:正切函数的图象叫做正切曲线.它是由被相互平行的直线所隔开的无穷多支完成相同的曲线组成的。因为正切函数是奇函数,所以正切曲线关于原点对称,此外,正切曲线是否还关于其它的点和直线对称?
知识探究(二):正切函数的性质
观察正切函数的图象,完成下列思考:
思考1:正切函数的定义域是
,
用区间表示为
思考2:根据诱导公式与周期函数的定义结合正切函数的图象,你能判断正切函数是周期函数吗?其最小正周期是什么??
思考3:根据图像你能判断正切函数具有奇偶性吗?
思考4:观察右图中的正切线,当角x在内增加时,
正切函数值发生什么变化?由此反映出一个什么性质?
思考5:结合正切函数的周期性,正切函数的单调性如何?
思考6:正切函数在整个定义域内是增函数吗?正切函数会不会在某一区间内是减函数?
思考7:正切函数的值域是什么?
三、典型例题
例1:比较下列两个三角函数值的大小.
(1)
(2)
变式练习1:比较下列两个三角函数值的大小.
(1)
(2)
例2:根据正切函数图象,分别写出满足下列条件的的集合:
(1)
(2)
(3)
变式练习2:(1)函数的定义域是
(2)函数的定义域是
例3:研究函数的基本性质
变式训练3:(1)求函数的基本性质
(2)求函数的定义域、周期和单调区间.
课后思考:研究函数的相关性质
课后练习与提高
1.
下列函数不等式中正确的是(
).
A.
B.
C.
D.
2.
若,则(
).
A.
B.
C.
D.
3.
函数的定义域为(
).
A.
B.
D.且
4.
函数的周期是
(
)
A.
B.
C.
D.
5.
函数的最小正周期是(
)
A.
B.
C.
D.
6.
函数的周期为(
).
A.
B.
C.
D.
7.
直线(a为常数)与正切曲线为常数,且相交的两相邻点间的距离为(
).
A.
B.
C.
D.与a值有关
8.
函数的定义域是(
)
A.
{且}
B.
{且}
C.
{且}
D.
{且}
9.
在下列函数中,同时满足:①在上递增;②以为周期;③是奇函数的是(
).
A.
B.
C.
D.
10.
的大小关系是
.
11.
函数的定义域为
.
12.
函数与的图像在上有
个交点。
13.
函数y=tan(的值域是
14.
求函数的定义域、值域,并指出它的奇偶性、单调性以及周期.
判断函数的奇偶性
16.
已知,求的最小值。
17.
已知(|x|≤)的最小值-4,求a的值.
