苏科版2019-2020学年九年级数学第二学期第6章:图形的相似 单元测试(含简略答案)
文档属性
| 名称 | 苏科版2019-2020学年九年级数学第二学期第6章:图形的相似 单元测试(含简略答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 255.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-03 00:00:00 | ||
图片预览


文档简介
苏科版
2019-2020
学年九年级数学第二学期图形的相似同步达标练习
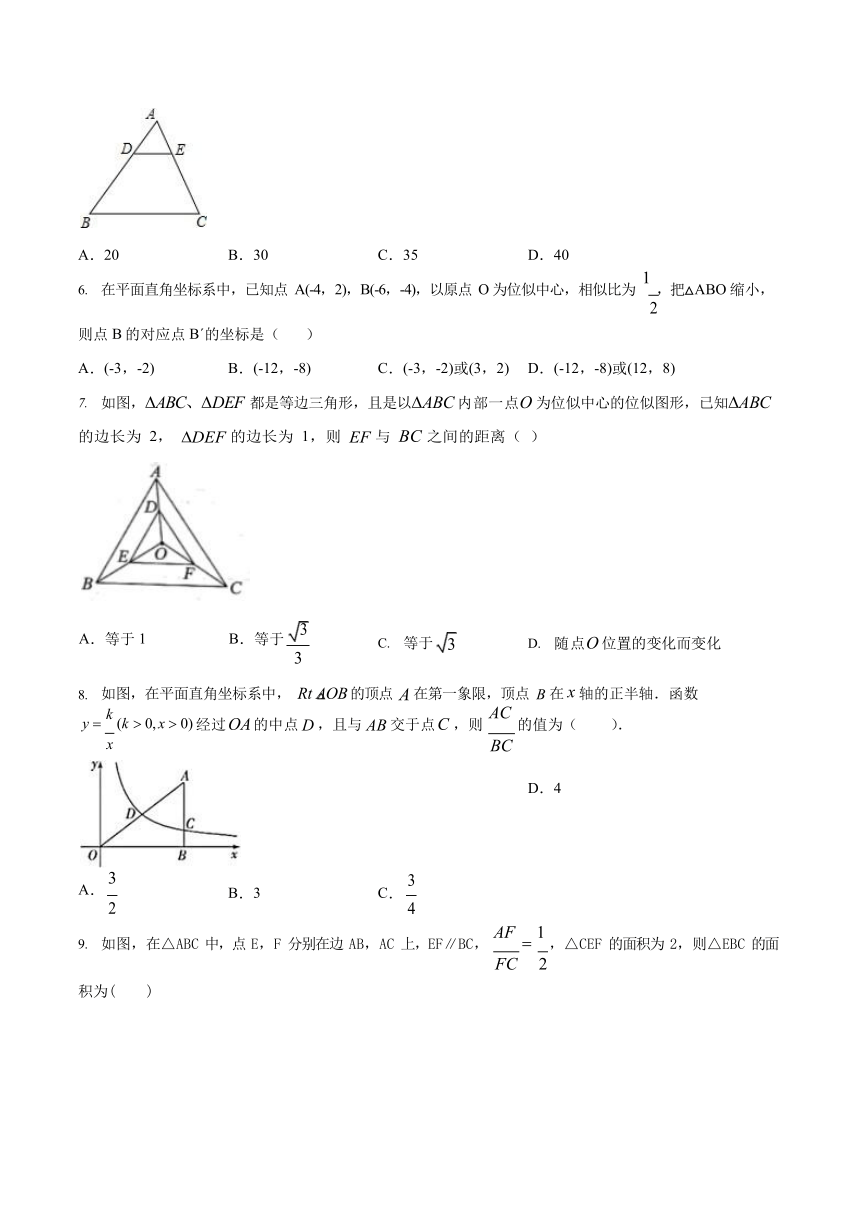
☆选择题(请在下面的四个选项中将正确的答案选在括号里)
如图,五边形
ABCDE
和五边形
A1B1C1D1E1
是位似图形,点
A
和点
A1
是一对对应点,P
是位似中心,且
2PA
3PA1
,则五边形
ABCDE
和五边形
A1B1C1D1E1
的相似比等于(
)
2
3
3
2
3
5
5
3
如图,小雅同学在利用标杆
BE
测量建筑物的高度时,测得标杆
BE
高1.2m
,又知
AB
:
BC
1:
8
,则建筑物CD
的高是(
)
A.9.6
m
B.10.8
m
C.12
m
D.14
m
如图,已知
DE
//
BC
则下列判断不正确的是()
AD
AE
AD
DE
AE
DE
DE
AD
D.
AB
AC
AB
BC
AC
BC
BC
BD
下列说法正确的是(
)
A.矩形都是相似图形;
B.菱形都是相似图形
C.各边对应成比例的多边形是相似多边形;
D.等边三角形都是相似三角形
如图,在△ABC
中,点
D
在边
AB
上,BD=2AD,DE∥BC
交
AC
于点
E,若△ADE
的周长为
10,则△ABC
的周长为(
)
A.20
B.30
C.35
D.40
在平面直角坐标系中,已知点
A(-4,2),B(-6,-4),以原点
O
为位似中心,相似比为
1
,把△ABO
缩小,
2
则点B
的对应点B?的坐标是(
)
A.(-3,-2)
B.(-12,-8)
C.(-3,-2)或(3,2)
D.(-12,-8)或(12,8)
如图,ABC、DEF
都是等边三角形,且是以ABC
内部一点O
为位似中心的位似图形,已知ABC
的边长为
2,
DEF
的边长为
1,则
EF
与
BC
之间的距离(
)
A.等于
1
B.等于
3
3
等于
随点O
位置的变化而变化
(
3
)如图,在平面直角坐标系中,
Rt
AOB
的顶点
A
在第一象限,顶点
B
在
x
轴的正半轴.函数
y
k
(k
0,
x
0)
经过OA
的中点
D
,且与
AB
交于点C
,则
AC
的值为(
).
x
BC
A.
3
2
3
B.3
C.
4
D.4
如图,在△ABC
中,点
E,F
分别在边
AB,AC
上,EF∥BC,
AF
1
,△CEF
的面积为
2,则△EBC
的面
积为(
)
FC
2
A.4
B.6
C.8
D.12
如图,反比例函数
y
k
(x
0)
的图象分别与矩形OABC
的边
AB
,BC
相交于点
D
,E
,与对角线OB
x
交于点
F
,以下结论:
①若△OAD
与△OCE
的面积和为
2,则k
2
;②若
B
点坐标为(4,
2)
,
AD
:
DB
1:
3
,则k
1;
③图中一定有
AD
CE
;④若点
F
是OB
的中点,且k
6
,则四边形ODBE
的面积为
18.
BD
BE
其中一定正确个数是(
)
A.1
B.2
C.3
D.4
☆填空题
如图,四边形
ABCD
内接于⊙O,对角线
AC、BD
交于点
P,且
AB=AD,若
AC=7,AB=3,则
BC?CD
=
.
在平面直角坐标系,点
A
坐标2,
4
,点
B
坐标4,
0
,点
P
是线段
AB
的中点,若以原点O
为位
似中心,把线段
AB
缩小为原来的
1
得到线段
AB
,则点
P
的对应点
P
坐标是
.
2
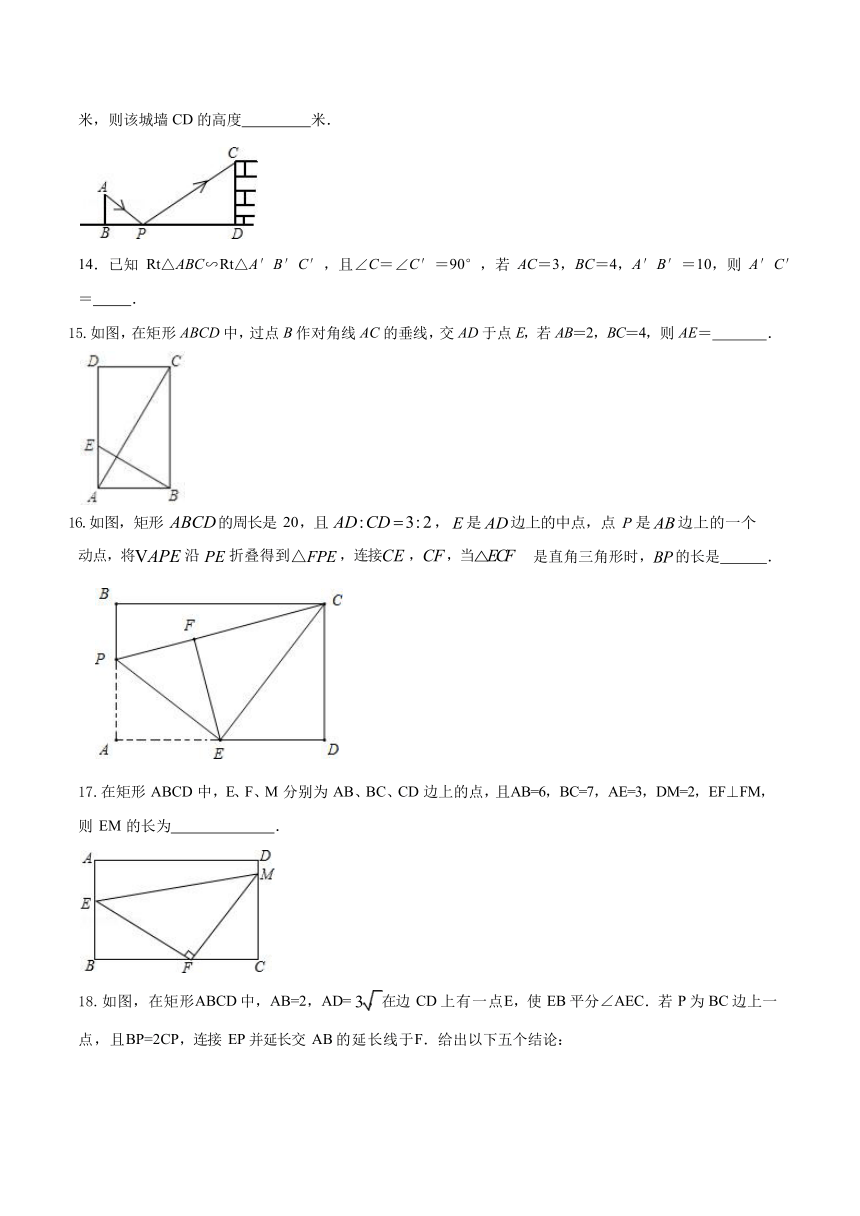
如图是小玲用手电来测量城墙高度的示意图.在点P
处水平放置平面镜,光线从点A
出发经平面镜反射后,刚好射到城墙
CD
的顶端C
处.已知
AB⊥BD,CD⊥BD,且测得
AB=1.4
米,BP=2.1
米,PD=12
米,则该城墙
CD
的高度
米.
14.已知
Rt△ABC∽Rt△A′B′C′,且∠C=∠C′=90°,若
AC=3,BC=4,A′B′=10,则
A′C′
=
.
15.如图,在矩形
ABCD
中,过点
B
作对角线
AC
的垂线,交
AD
于点
E,若
AB=2,BC=4,则
AE=
.
16.如图,矩形
ABCD
的周长是
20,且
AD
:
CD
3:
2
,
E
是
AD
边上的中点,点
P
是
AB
边上的一个
动点,将VAPE
沿
PE
折叠得到△FPE
,连接CE
,CF
,当△ECF
是直角三角形时,BP
的长是
.
17.在矩形
ABCD
中,E、F、M
分别为
AB、BC、CD
边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则
EM
的长为
.
18.如图,在矩形ABCD
中,AB=2,AD=
3
,在边
CD
上有一点E,使
EB
平分∠AEC.若
P
为
BC
边上一点,且BP=2CP,连接
EP
并延长交
AB
的延长线于F.给出以下五个结论:
(
4
3
3
)①点B
平分线段AF;②PF=
DE;③∠BEF=∠FEC;④S
矩形ABCD=4S△BPF;⑤△AEB
是正三角形.其中
正确结论的序号是
.
☆解答题
19.如图,
ABC
中,点
D
在
AB
上,AD
1,点
E
在
AC
上,满足AED
B
,求
AC
的长.
20.如图,小华在晚上由路灯
A
走向路灯
B.当他走到点
P
时,发现他身后影子的顶部刚好接触到路灯
A
的底部;当他向前再步行
12m
到达点
Q
时,发现他身前影子的顶部刚好接触到路灯
B
的底部.已知小华的身高是
1.6m,两个路灯的高度都是
9.6m,且
AP=QB.
求两个路灯之间的距离;
当小华走到路灯
B
的底部时,他在路灯
A
下的影长是多少?
21.如图,△ABC
中,AB=AC,AD⊥BC
于点D,DE⊥AC
于点
E,CF⊥AB
于点
F.
求证:△BCF∽△CDE;
若
DE=3,求
CF
的长.
22.如图,在等腰
ABC
中,
AC
BC,
以
BC
为直径的
O
与底边
AB
交于点
D,
过
D
作
O
的切线C
于点
E
.
证明:
DE
AC
;
若
BC
8,
AD
6,
求
AE
的长.
23.如图,在平行四边形
ABCD
中,点
G
在边
DC
的延长线上,AG
交边
BC
于点
E,交对角线
BD
于点
F.
求证:AF2=EF?FG;
如果EF=
3
2
,FG=
8
,求
BE
3
EC
的值.
24.如图①,△ABC
是等腰直角三角形,在两腰
AB、AC
外侧作两个等边三角形
ABD
和
ACE,AM
和
AN
分别是等边三角形
ABD
和
ACE
的角平分线,连接
CM、BN,CM
与
AB
交于点
P.
求证:CM=BN;
如图②,点
F
为角平分线
AN
上一点,且∠CPF=30°,求证:△APF∽△AMC;
PF
在(2)的条件下,求
BN
的值.
25.如图,
AB
是⊙
O
的直径,弦CD
AB
于点
H
,连接
AC
,过弧
BD
上一点
E
作
EG
//
AC
交CD
的延长线于点G
,连接
AE
交CD
于点
F
,且
EG
FG
,连接CE
.
求证:
ECF
GCE
;
求证:
EG
是⊙
O
的切线;
延长
AB
交GE
的延长线于点
M
,若tan
G
3
,
ah
3
3
,求
EM
的值.
4
26.如图,在平面直角坐标中,抛物线
y=ax2+bx+c
过点
A(﹣1,0),B(3,0),C(0,3),点
P
是直线
BC
上方抛物线上的一动点,PE∥y
轴,交直线
BC
于点
E
连接
AP,交直线
BC
于点
D.
求抛物线的函数表达式;
当
AD=2PD
时,求点P
的坐标;
求线段PE
的最大值;
当线段PE
最大时,若点
F
在直线
BC
上且∠EFP=2∠ACO,直接写出点F
的坐标.
参考答案
1.B2.B3.D4.D5.B6.C7.D8.B9.B10.C
11.40.
12.
略
13.8
14.6.
15.1
16.
9
或
3
4
(
2
)17.5
.
18.①②③⑤
AC
5
2
(1)两个路灯之间的距离为
18m.
(2)当小华走到路灯
B
的底部时,他在路灯
A
下的影长是
3.6m.
21.(1)证明略;(2)6.
(
9
)22.(1)证明略;(2)
AE
.
2
23.(1)略;(2)
BE
=3.
EC
24.(1)略(2)略(3)
8
3
6
13
25.(1)略;(2)略;(3)
EM
25
3
8
26.(1)y=﹣x2+2x+3;(2)P(1,4)或
P(2,3);(3)(﹣
9
,
33
)或(
15
,
9
)
8
8
8
8
2019-2020
学年九年级数学第二学期图形的相似同步达标练习
☆选择题(请在下面的四个选项中将正确的答案选在括号里)
如图,五边形
ABCDE
和五边形
A1B1C1D1E1
是位似图形,点
A
和点
A1
是一对对应点,P
是位似中心,且
2PA
3PA1
,则五边形
ABCDE
和五边形
A1B1C1D1E1
的相似比等于(
)
2
3
3
2
3
5
5
3
如图,小雅同学在利用标杆
BE
测量建筑物的高度时,测得标杆
BE
高1.2m
,又知
AB
:
BC
1:
8
,则建筑物CD
的高是(
)
A.9.6
m
B.10.8
m
C.12
m
D.14
m
如图,已知
DE
//
BC
则下列判断不正确的是()
AD
AE
AD
DE
AE
DE
DE
AD
D.
AB
AC
AB
BC
AC
BC
BC
BD
下列说法正确的是(
)
A.矩形都是相似图形;
B.菱形都是相似图形
C.各边对应成比例的多边形是相似多边形;
D.等边三角形都是相似三角形
如图,在△ABC
中,点
D
在边
AB
上,BD=2AD,DE∥BC
交
AC
于点
E,若△ADE
的周长为
10,则△ABC
的周长为(
)
A.20
B.30
C.35
D.40
在平面直角坐标系中,已知点
A(-4,2),B(-6,-4),以原点
O
为位似中心,相似比为
1
,把△ABO
缩小,
2
则点B
的对应点B?的坐标是(
)
A.(-3,-2)
B.(-12,-8)
C.(-3,-2)或(3,2)
D.(-12,-8)或(12,8)
如图,ABC、DEF
都是等边三角形,且是以ABC
内部一点O
为位似中心的位似图形,已知ABC
的边长为
2,
DEF
的边长为
1,则
EF
与
BC
之间的距离(
)
A.等于
1
B.等于
3
3
等于
随点O
位置的变化而变化
(
3
)如图,在平面直角坐标系中,
Rt
AOB
的顶点
A
在第一象限,顶点
B
在
x
轴的正半轴.函数
y
k
(k
0,
x
0)
经过OA
的中点
D
,且与
AB
交于点C
,则
AC
的值为(
).
x
BC
A.
3
2
3
B.3
C.
4
D.4
如图,在△ABC
中,点
E,F
分别在边
AB,AC
上,EF∥BC,
AF
1
,△CEF
的面积为
2,则△EBC
的面
积为(
)
FC
2
A.4
B.6
C.8
D.12
如图,反比例函数
y
k
(x
0)
的图象分别与矩形OABC
的边
AB
,BC
相交于点
D
,E
,与对角线OB
x
交于点
F
,以下结论:
①若△OAD
与△OCE
的面积和为
2,则k
2
;②若
B
点坐标为(4,
2)
,
AD
:
DB
1:
3
,则k
1;
③图中一定有
AD
CE
;④若点
F
是OB
的中点,且k
6
,则四边形ODBE
的面积为
18.
BD
BE
其中一定正确个数是(
)
A.1
B.2
C.3
D.4
☆填空题
如图,四边形
ABCD
内接于⊙O,对角线
AC、BD
交于点
P,且
AB=AD,若
AC=7,AB=3,则
BC?CD
=
.
在平面直角坐标系,点
A
坐标2,
4
,点
B
坐标4,
0
,点
P
是线段
AB
的中点,若以原点O
为位
似中心,把线段
AB
缩小为原来的
1
得到线段
AB
,则点
P
的对应点
P
坐标是
.
2
如图是小玲用手电来测量城墙高度的示意图.在点P
处水平放置平面镜,光线从点A
出发经平面镜反射后,刚好射到城墙
CD
的顶端C
处.已知
AB⊥BD,CD⊥BD,且测得
AB=1.4
米,BP=2.1
米,PD=12
米,则该城墙
CD
的高度
米.
14.已知
Rt△ABC∽Rt△A′B′C′,且∠C=∠C′=90°,若
AC=3,BC=4,A′B′=10,则
A′C′
=
.
15.如图,在矩形
ABCD
中,过点
B
作对角线
AC
的垂线,交
AD
于点
E,若
AB=2,BC=4,则
AE=
.
16.如图,矩形
ABCD
的周长是
20,且
AD
:
CD
3:
2
,
E
是
AD
边上的中点,点
P
是
AB
边上的一个
动点,将VAPE
沿
PE
折叠得到△FPE
,连接CE
,CF
,当△ECF
是直角三角形时,BP
的长是
.
17.在矩形
ABCD
中,E、F、M
分别为
AB、BC、CD
边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则
EM
的长为
.
18.如图,在矩形ABCD
中,AB=2,AD=
3
,在边
CD
上有一点E,使
EB
平分∠AEC.若
P
为
BC
边上一点,且BP=2CP,连接
EP
并延长交
AB
的延长线于F.给出以下五个结论:
(
4
3
3
)①点B
平分线段AF;②PF=
DE;③∠BEF=∠FEC;④S
矩形ABCD=4S△BPF;⑤△AEB
是正三角形.其中
正确结论的序号是
.
☆解答题
19.如图,
ABC
中,点
D
在
AB
上,AD
1,点
E
在
AC
上,满足AED
B
,求
AC
的长.
20.如图,小华在晚上由路灯
A
走向路灯
B.当他走到点
P
时,发现他身后影子的顶部刚好接触到路灯
A
的底部;当他向前再步行
12m
到达点
Q
时,发现他身前影子的顶部刚好接触到路灯
B
的底部.已知小华的身高是
1.6m,两个路灯的高度都是
9.6m,且
AP=QB.
求两个路灯之间的距离;
当小华走到路灯
B
的底部时,他在路灯
A
下的影长是多少?
21.如图,△ABC
中,AB=AC,AD⊥BC
于点D,DE⊥AC
于点
E,CF⊥AB
于点
F.
求证:△BCF∽△CDE;
若
DE=3,求
CF
的长.
22.如图,在等腰
ABC
中,
AC
BC,
以
BC
为直径的
O
与底边
AB
交于点
D,
过
D
作
O
的切线C
于点
E
.
证明:
DE
AC
;
若
BC
8,
AD
6,
求
AE
的长.
23.如图,在平行四边形
ABCD
中,点
G
在边
DC
的延长线上,AG
交边
BC
于点
E,交对角线
BD
于点
F.
求证:AF2=EF?FG;
如果EF=
3
2
,FG=
8
,求
BE
3
EC
的值.
24.如图①,△ABC
是等腰直角三角形,在两腰
AB、AC
外侧作两个等边三角形
ABD
和
ACE,AM
和
AN
分别是等边三角形
ABD
和
ACE
的角平分线,连接
CM、BN,CM
与
AB
交于点
P.
求证:CM=BN;
如图②,点
F
为角平分线
AN
上一点,且∠CPF=30°,求证:△APF∽△AMC;
PF
在(2)的条件下,求
BN
的值.
25.如图,
AB
是⊙
O
的直径,弦CD
AB
于点
H
,连接
AC
,过弧
BD
上一点
E
作
EG
//
AC
交CD
的延长线于点G
,连接
AE
交CD
于点
F
,且
EG
FG
,连接CE
.
求证:
ECF
GCE
;
求证:
EG
是⊙
O
的切线;
延长
AB
交GE
的延长线于点
M
,若tan
G
3
,
ah
3
3
,求
EM
的值.
4
26.如图,在平面直角坐标中,抛物线
y=ax2+bx+c
过点
A(﹣1,0),B(3,0),C(0,3),点
P
是直线
BC
上方抛物线上的一动点,PE∥y
轴,交直线
BC
于点
E
连接
AP,交直线
BC
于点
D.
求抛物线的函数表达式;
当
AD=2PD
时,求点P
的坐标;
求线段PE
的最大值;
当线段PE
最大时,若点
F
在直线
BC
上且∠EFP=2∠ACO,直接写出点F
的坐标.
参考答案
1.B2.B3.D4.D5.B6.C7.D8.B9.B10.C
11.40.
12.
略
13.8
14.6.
15.1
16.
9
或
3
4
(
2
)17.5
.
18.①②③⑤
AC
5
2
(1)两个路灯之间的距离为
18m.
(2)当小华走到路灯
B
的底部时,他在路灯
A
下的影长是
3.6m.
21.(1)证明略;(2)6.
(
9
)22.(1)证明略;(2)
AE
.
2
23.(1)略;(2)
BE
=3.
EC
24.(1)略(2)略(3)
8
3
6
13
25.(1)略;(2)略;(3)
EM
25
3
8
26.(1)y=﹣x2+2x+3;(2)P(1,4)或
P(2,3);(3)(﹣
9
,
33
)或(
15
,
9
)
8
8
8
8
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
