北师大版七年级数学下册——构造(证明)全等三角形常用方法与技巧学案(含答案)
文档属性
| 名称 | 北师大版七年级数学下册——构造(证明)全等三角形常用方法与技巧学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 443.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-03 17:27:44 | ||
图片预览

文档简介
第四章
构造(证明)全等三角形常用方法与技巧
翻折法
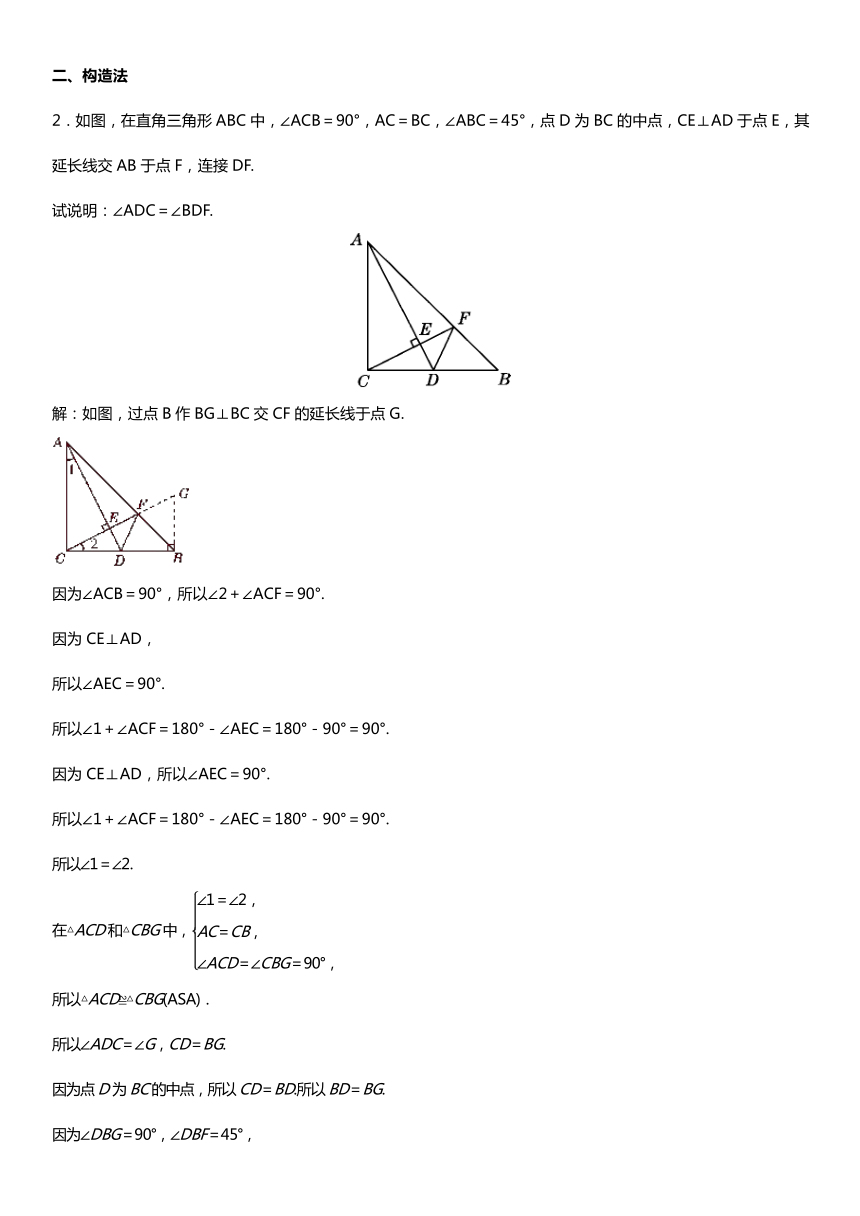
1.如图,在△ABC中,BE是∠ABC的平分线,AD⊥BE,垂足为D.试说明:∠2=∠1+∠C.
解:如图,过点B作BG⊥BC交CF的延长线于点G.
因为∠ACB=90°,所以∠2+∠ACF=90°.
因为CE⊥AD,
所以∠AEC=90°.
所以∠1+∠ACF=180°-∠AEC=180°-90°=90°.
因为CE⊥AD,所以∠AEC=90°.
所以∠1+∠ACF=180°-∠AEC=180°-90°=90°.
在△ABD和△FBD中,
所以△ABD≌△FBD(ASA).所以∠2=∠DFB.
又因为∠DFB=180°-∠AFC,
∠1+∠C=180°-∠AFC,
所以∠DFB=∠1+∠C.所以∠2=∠1+∠C.
构造法
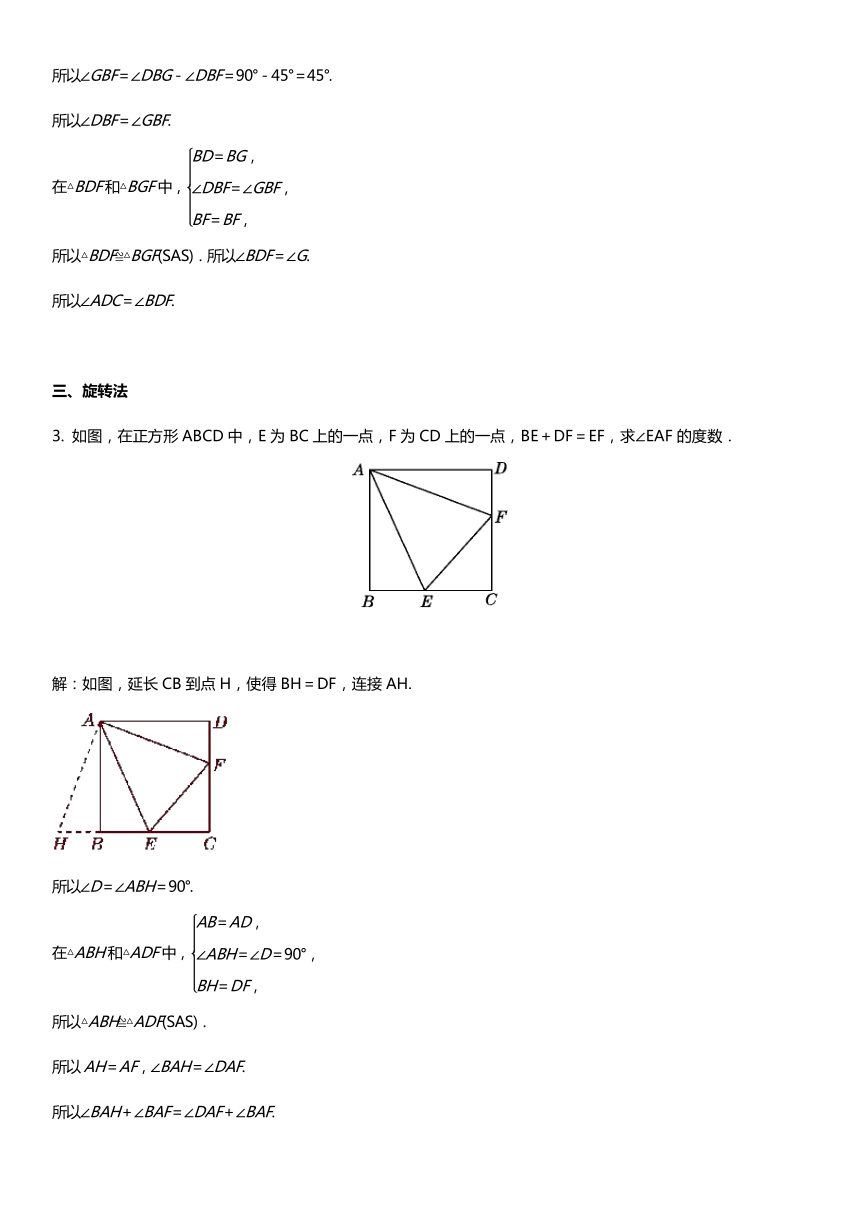
2.如图,在直角三角形ABC中,∠ACB=90°,AC=BC,∠ABC=45°,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.
试说明:∠ADC=∠BDF.
解:如图,过点B作BG⊥BC交CF的延长线于点G.
因为∠ACB=90°,所以∠2+∠ACF=90°.
因为CE⊥AD,
所以∠AEC=90°.
所以∠1+∠ACF=180°-∠AEC=180°-90°=90°.
因为CE⊥AD,所以∠AEC=90°.
所以∠1+∠ACF=180°-∠AEC=180°-90°=90°.
所以∠1=∠2.
在△ACD和△CBG中,
所以△ACD≌△CBG(ASA).
所以∠ADC=∠G,CD=BG.
因为点D为BC的中点,所以CD=BD.所以BD=BG.
因为∠DBG=90°,∠DBF=45°,
所以∠GBF=∠DBG-∠DBF=90°-45°=45°.
所以∠DBF=∠GBF.
在△BDF和△BGF中,
所以△BDF≌△BGF(SAS).所以∠BDF=∠G.
所以∠ADC=∠BDF.
旋转法
如图,在正方形ABCD中,E为BC上的一点,F为CD上的一点,BE+DF=EF,求∠EAF的度数.
解:如图,延长CB到点H,使得BH=DF,连接AH.
所以∠D=∠ABH=90°.
在△ABH和△ADF中,
所以△ABH≌△ADF(SAS).
所以AH=AF,∠BAH=∠DAF.
所以∠BAH+∠BAF=∠DAF+∠BAF.
所以∠HAF=∠BAD=90°.
因为BE+DF=EF,所以BE+BH=EF,即EH=EF.
在△AEH和△AEF中,
所以△AEH≌△AEF(SSS).
所以∠EAH=∠EAF.
所以∠EAF=∠HAF=45°.
倍长中线法
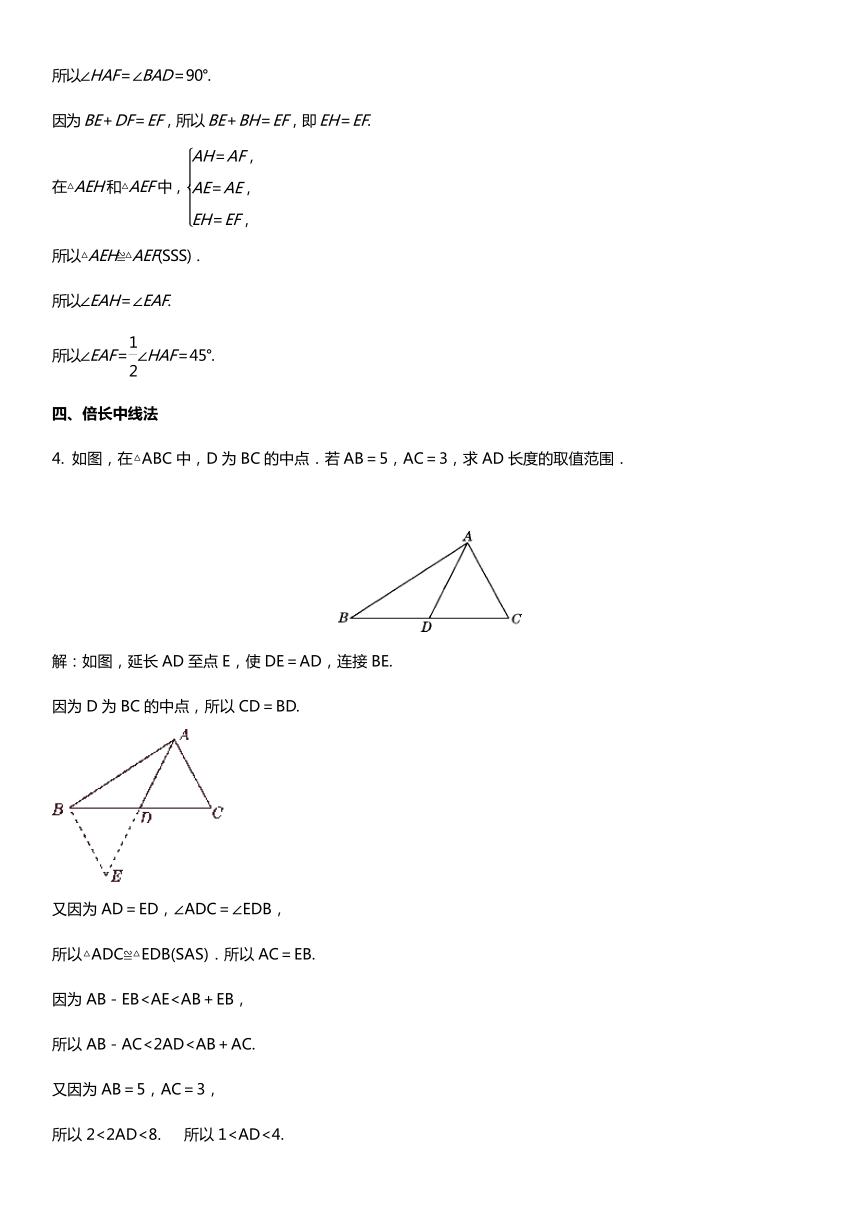
如图,在△ABC中,D为BC的中点.若AB=5,AC=3,求AD长度的取值范围.
解:如图,延长AD至点E,使DE=AD,连接BE.
因为D为BC的中点,所以CD=BD.
又因为AD=ED,∠ADC=∠EDB,
所以△ADC≌△EDB(SAS).所以AC=EB.
因为AB-EB所以AB-AC<2AD又因为AB=5,AC=3,
所以2<2AD<8.
所以1截长补短法
5.如图,在正方形ABCD中,E是AB上一点,点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
解:成立.理由如下:
如图,延长AD至F,使DF=BE,连接CF.
在正方形ABCD中,BC=DC,∠B=∠CDA=90°,
所以∠CDF=∠B=90°.
又因为BE=DF,所以△CBE≌△CDF(SAS).
所以CE=CF,∠BCE=∠DCF.
所以∠BCE+∠ECD=∠DCF+∠ECD.所以∠ECF=∠BCD=90°.
因为∠GCE=45°,所以∠GCF=∠GCE=45°.
又因为CE=CF,GC=GC,
所以△ECG≌△FCG(SAS).所以GE=GF.
所以GE=DF+GD=BE+GD.
综合练习
如图,在△ABC中,D是AB上一点,DF交AC于点E,AE=EC,DE=EF,则下列结论中:①∠ADE=∠EFC;②∠ADE+∠ECF+∠FEC=180°;③∠B+∠BCF=180°;④S△ABC=S四边形DBCF,正确的结论有(
)
A.4个
B.3个
C.2个
D.1个
2.如图,D,E,F分别为AB,AC,BC上的点,且DE∥BC,△ABC沿线段DE折叠,使点A落在点F处.若∠B=50°,则∠BDF=________.
3.如图,已知边长为1的正方形ABCD,AC,BD交于点O,过点O任作一条直线分别交AD,BC于点E,F,则阴影部分的面积是________.
4.如图,AD,AE分别是△ABC的角平分线、高线,且∠B=50°,∠C=70°,则∠EAD=________.
5.如图,已知四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,且AE=(AB+AD),若∠D=115°,则∠B=________.
6.如图①,在Rt△ABC中,AB=AC,∠BAC=90°,过点A的直线l绕点A旋转,BD⊥l于D,CE⊥l于E.
(1)试说明:DE=BD+CE.
(2)当直线l绕点A旋转到如图②所示的位置时,(1)中结论是否成立?若成立,请说明;若不成立,请探究DE,BD,CE又有怎样的数量关系,并写出探究过程.
INCLUDEPICTURE"AS36.tif"
INCLUDEPICTURE
"C:\\Users\\Administrator\\Desktop\\公司后半周期\\7数学BS\\word\\AS36.tif"
\
MERGEFORMATINET
INCLUDEPICTURE
"C:\\Users\\Administrator\\Desktop\\公司后半周期\\7数学BS\\word\\AS36.tif"
\
MERGEFORMATINET
7.在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.设∠BAC=α,∠DCE=β.
(1)如图①,点D在线段BC上移动时,角α与β之间的数量关系是____________,请说明理由;
(2)如图②,点D在线段BC的延长线上移动时,角α与β之间的数量关系是____________,请说明理由;
(3)当点D在线段BC的反向延长线上移动时,请在图③中画出完整图形并猜想角α与β之间的数量关系是________________.
INCLUDEPICTURE"AS49.tif"
INCLUDEPICTURE
"C:\\Users\\Administrator\\Desktop\\公司后半周期\\7数学BS\\word\\AS49.tif"
\
MERGEFORMATINET
INCLUDEPICTURE
"C:\\Users\\Administrator\\Desktop\\公司后半周期\\7数学BS\\word\\AS49.tif"
\
MERGEFORMATINET
INCLUDEPICTURE
"C:\\Users\\Administrator\\Desktop\\公司后半周期\\7数学BS\\word\\AS49.tif"
\
MERGEFORMATINET
参考答案
1.A
2.80° 3.
4.10° 点拨:由AD平分∠BAC,可得∠DAC=∠BAC=×(180°-50°-70°)=30°.由AE⊥BC,可得∠EAC=90°-∠C=20°,所以∠EAD=30°-20°=10°.
5.65° 点拨:过C作CF⊥AD,交AD的延长线于F.
因为AC平分∠BAD,
所以∠CAF=∠CAE.
因为CF⊥AF,CE⊥AB,
所以∠AFC=∠AEC=90°.
在△CAF和△CAE中,
所以△CAF≌△CAE(AAS).
所以FC=EC,AF=AE.
因为AE=(AB+AD),
所以AF=(AE+EB+AD),
即AF=BE+AD.
所以DF=BE.
在△FDC和△EBC中,
所以△FDC≌△EBC(SAS).
所以∠FDC=∠EBC.
又因为∠ADC=115°,
所以∠FDC=180°-115°=65°.
所以∠B=65°.
6.解:(1)因为BD⊥l,CE⊥l,
所以∠ADB=∠AEC=90°.
所以∠DBA+∠BAD=90°.
又因为∠BAC=90°,
所以∠BAD+∠CAE=90°.
所以∠DBA=∠CAE.
因为AB=AC,∠ADB=∠CEA=90°,
所以△ABD≌△CAE(AAS).
所以AD=CE,BD=AE.
则AD+AE=BD+CE,
即DE=BD+CE.
(2)(1)中结论不成立.
DE=BD-CE.
同(1)说明△ABD≌△CAE,
所以BD=AE,AD=CE.
又因为AE-AD=DE,
所以DE=BD-CE.
7.解:(1)α+β=180°
理由:因为∠DAE=∠BAC,
所以∠DAE-∠CAD=∠BAC-∠CAD,即∠BAD=∠CAE.
又因为AB=AC,AD=AE,
所以△ABD≌△ACE(SAS).
所以∠ABC=∠ACE.
在△ABC中,∠BAC+∠ABC+∠ACB=180°,∠ABC=∠ACE,
所以∠BAC+∠ACB+∠ACE=180°.
因为∠ACB+∠ACE=∠DCE=β,
所以α+β=180°.
(2)α=β
理由:因为∠DAE=∠BAC,
所以∠BAD=∠CAE.
又因为AB=AC,AD=AE,
所以△ABD≌△ACE(SAS).
所以∠ABC=∠ACE.
因为∠ABC+∠BAC+∠ACB=180°,∠ACB+∠ACD=180°,
所以∠ACD=∠ABC+∠BAC=∠ACE+∠ECD.
所以∠BAC=∠ECD.
所以α=β.
(3)α=β.画图略.
构造(证明)全等三角形常用方法与技巧
翻折法
1.如图,在△ABC中,BE是∠ABC的平分线,AD⊥BE,垂足为D.试说明:∠2=∠1+∠C.
解:如图,过点B作BG⊥BC交CF的延长线于点G.
因为∠ACB=90°,所以∠2+∠ACF=90°.
因为CE⊥AD,
所以∠AEC=90°.
所以∠1+∠ACF=180°-∠AEC=180°-90°=90°.
因为CE⊥AD,所以∠AEC=90°.
所以∠1+∠ACF=180°-∠AEC=180°-90°=90°.
在△ABD和△FBD中,
所以△ABD≌△FBD(ASA).所以∠2=∠DFB.
又因为∠DFB=180°-∠AFC,
∠1+∠C=180°-∠AFC,
所以∠DFB=∠1+∠C.所以∠2=∠1+∠C.
构造法
2.如图,在直角三角形ABC中,∠ACB=90°,AC=BC,∠ABC=45°,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.
试说明:∠ADC=∠BDF.
解:如图,过点B作BG⊥BC交CF的延长线于点G.
因为∠ACB=90°,所以∠2+∠ACF=90°.
因为CE⊥AD,
所以∠AEC=90°.
所以∠1+∠ACF=180°-∠AEC=180°-90°=90°.
因为CE⊥AD,所以∠AEC=90°.
所以∠1+∠ACF=180°-∠AEC=180°-90°=90°.
所以∠1=∠2.
在△ACD和△CBG中,
所以△ACD≌△CBG(ASA).
所以∠ADC=∠G,CD=BG.
因为点D为BC的中点,所以CD=BD.所以BD=BG.
因为∠DBG=90°,∠DBF=45°,
所以∠GBF=∠DBG-∠DBF=90°-45°=45°.
所以∠DBF=∠GBF.
在△BDF和△BGF中,
所以△BDF≌△BGF(SAS).所以∠BDF=∠G.
所以∠ADC=∠BDF.
旋转法
如图,在正方形ABCD中,E为BC上的一点,F为CD上的一点,BE+DF=EF,求∠EAF的度数.
解:如图,延长CB到点H,使得BH=DF,连接AH.
所以∠D=∠ABH=90°.
在△ABH和△ADF中,
所以△ABH≌△ADF(SAS).
所以AH=AF,∠BAH=∠DAF.
所以∠BAH+∠BAF=∠DAF+∠BAF.
所以∠HAF=∠BAD=90°.
因为BE+DF=EF,所以BE+BH=EF,即EH=EF.
在△AEH和△AEF中,
所以△AEH≌△AEF(SSS).
所以∠EAH=∠EAF.
所以∠EAF=∠HAF=45°.
倍长中线法
如图,在△ABC中,D为BC的中点.若AB=5,AC=3,求AD长度的取值范围.
解:如图,延长AD至点E,使DE=AD,连接BE.
因为D为BC的中点,所以CD=BD.
又因为AD=ED,∠ADC=∠EDB,
所以△ADC≌△EDB(SAS).所以AC=EB.
因为AB-EB
所以2<2AD<8.
所以1
5.如图,在正方形ABCD中,E是AB上一点,点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
解:成立.理由如下:
如图,延长AD至F,使DF=BE,连接CF.
在正方形ABCD中,BC=DC,∠B=∠CDA=90°,
所以∠CDF=∠B=90°.
又因为BE=DF,所以△CBE≌△CDF(SAS).
所以CE=CF,∠BCE=∠DCF.
所以∠BCE+∠ECD=∠DCF+∠ECD.所以∠ECF=∠BCD=90°.
因为∠GCE=45°,所以∠GCF=∠GCE=45°.
又因为CE=CF,GC=GC,
所以△ECG≌△FCG(SAS).所以GE=GF.
所以GE=DF+GD=BE+GD.
综合练习
如图,在△ABC中,D是AB上一点,DF交AC于点E,AE=EC,DE=EF,则下列结论中:①∠ADE=∠EFC;②∠ADE+∠ECF+∠FEC=180°;③∠B+∠BCF=180°;④S△ABC=S四边形DBCF,正确的结论有(
)
A.4个
B.3个
C.2个
D.1个
2.如图,D,E,F分别为AB,AC,BC上的点,且DE∥BC,△ABC沿线段DE折叠,使点A落在点F处.若∠B=50°,则∠BDF=________.
3.如图,已知边长为1的正方形ABCD,AC,BD交于点O,过点O任作一条直线分别交AD,BC于点E,F,则阴影部分的面积是________.
4.如图,AD,AE分别是△ABC的角平分线、高线,且∠B=50°,∠C=70°,则∠EAD=________.
5.如图,已知四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,且AE=(AB+AD),若∠D=115°,则∠B=________.
6.如图①,在Rt△ABC中,AB=AC,∠BAC=90°,过点A的直线l绕点A旋转,BD⊥l于D,CE⊥l于E.
(1)试说明:DE=BD+CE.
(2)当直线l绕点A旋转到如图②所示的位置时,(1)中结论是否成立?若成立,请说明;若不成立,请探究DE,BD,CE又有怎样的数量关系,并写出探究过程.
INCLUDEPICTURE"AS36.tif"
INCLUDEPICTURE
"C:\\Users\\Administrator\\Desktop\\公司后半周期\\7数学BS\\word\\AS36.tif"
\
MERGEFORMATINET
INCLUDEPICTURE
"C:\\Users\\Administrator\\Desktop\\公司后半周期\\7数学BS\\word\\AS36.tif"
\
MERGEFORMATINET
7.在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.设∠BAC=α,∠DCE=β.
(1)如图①,点D在线段BC上移动时,角α与β之间的数量关系是____________,请说明理由;
(2)如图②,点D在线段BC的延长线上移动时,角α与β之间的数量关系是____________,请说明理由;
(3)当点D在线段BC的反向延长线上移动时,请在图③中画出完整图形并猜想角α与β之间的数量关系是________________.
INCLUDEPICTURE"AS49.tif"
INCLUDEPICTURE
"C:\\Users\\Administrator\\Desktop\\公司后半周期\\7数学BS\\word\\AS49.tif"
\
MERGEFORMATINET
INCLUDEPICTURE
"C:\\Users\\Administrator\\Desktop\\公司后半周期\\7数学BS\\word\\AS49.tif"
\
MERGEFORMATINET
INCLUDEPICTURE
"C:\\Users\\Administrator\\Desktop\\公司后半周期\\7数学BS\\word\\AS49.tif"
\
MERGEFORMATINET
参考答案
1.A
2.80° 3.
4.10° 点拨:由AD平分∠BAC,可得∠DAC=∠BAC=×(180°-50°-70°)=30°.由AE⊥BC,可得∠EAC=90°-∠C=20°,所以∠EAD=30°-20°=10°.
5.65° 点拨:过C作CF⊥AD,交AD的延长线于F.
因为AC平分∠BAD,
所以∠CAF=∠CAE.
因为CF⊥AF,CE⊥AB,
所以∠AFC=∠AEC=90°.
在△CAF和△CAE中,
所以△CAF≌△CAE(AAS).
所以FC=EC,AF=AE.
因为AE=(AB+AD),
所以AF=(AE+EB+AD),
即AF=BE+AD.
所以DF=BE.
在△FDC和△EBC中,
所以△FDC≌△EBC(SAS).
所以∠FDC=∠EBC.
又因为∠ADC=115°,
所以∠FDC=180°-115°=65°.
所以∠B=65°.
6.解:(1)因为BD⊥l,CE⊥l,
所以∠ADB=∠AEC=90°.
所以∠DBA+∠BAD=90°.
又因为∠BAC=90°,
所以∠BAD+∠CAE=90°.
所以∠DBA=∠CAE.
因为AB=AC,∠ADB=∠CEA=90°,
所以△ABD≌△CAE(AAS).
所以AD=CE,BD=AE.
则AD+AE=BD+CE,
即DE=BD+CE.
(2)(1)中结论不成立.
DE=BD-CE.
同(1)说明△ABD≌△CAE,
所以BD=AE,AD=CE.
又因为AE-AD=DE,
所以DE=BD-CE.
7.解:(1)α+β=180°
理由:因为∠DAE=∠BAC,
所以∠DAE-∠CAD=∠BAC-∠CAD,即∠BAD=∠CAE.
又因为AB=AC,AD=AE,
所以△ABD≌△ACE(SAS).
所以∠ABC=∠ACE.
在△ABC中,∠BAC+∠ABC+∠ACB=180°,∠ABC=∠ACE,
所以∠BAC+∠ACB+∠ACE=180°.
因为∠ACB+∠ACE=∠DCE=β,
所以α+β=180°.
(2)α=β
理由:因为∠DAE=∠BAC,
所以∠BAD=∠CAE.
又因为AB=AC,AD=AE,
所以△ABD≌△ACE(SAS).
所以∠ABC=∠ACE.
因为∠ABC+∠BAC+∠ACB=180°,∠ACB+∠ACD=180°,
所以∠ACD=∠ABC+∠BAC=∠ACE+∠ECD.
所以∠BAC=∠ECD.
所以α=β.
(3)α=β.画图略.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
