(四川)2020--2021物理人教版选修3-3课件:第八章 气体18张
文档属性
| 名称 | (四川)2020--2021物理人教版选修3-3课件:第八章 气体18张 |

|
|
| 格式 | zip | ||
| 文件大小 | 636.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-06-03 18:04:03 | ||
图片预览



文档简介
(共18张PPT)
第八章 气体整合
思考并回答下列问题
本章知识可分为两个单元。第一单元,气体实验三定律,包括玻意耳定律、查理定律和盖—吕萨克定律;第二单元:理想气体状态方程和气体热现象的微观意义。
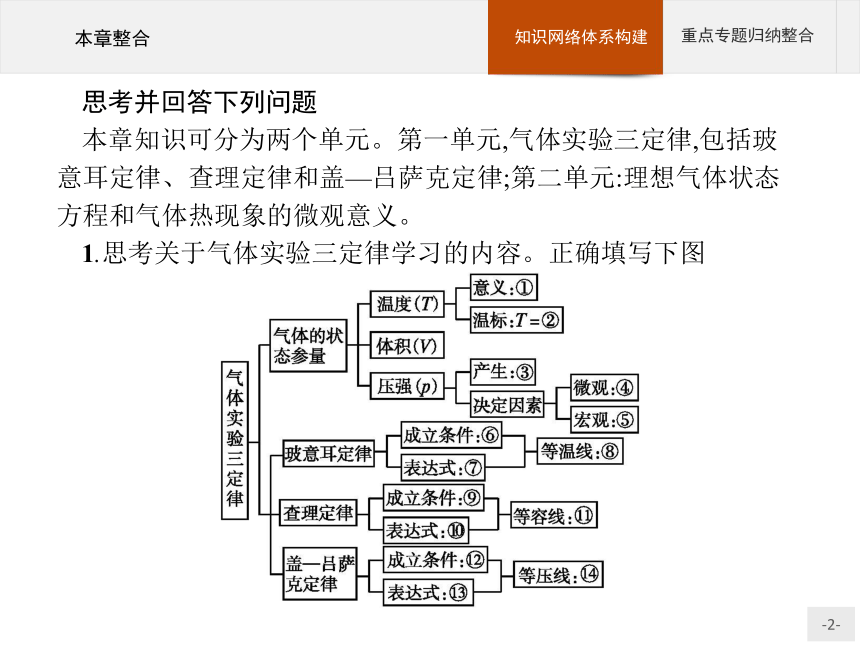
1.思考关于气体实验三定律学习的内容。正确填写下图
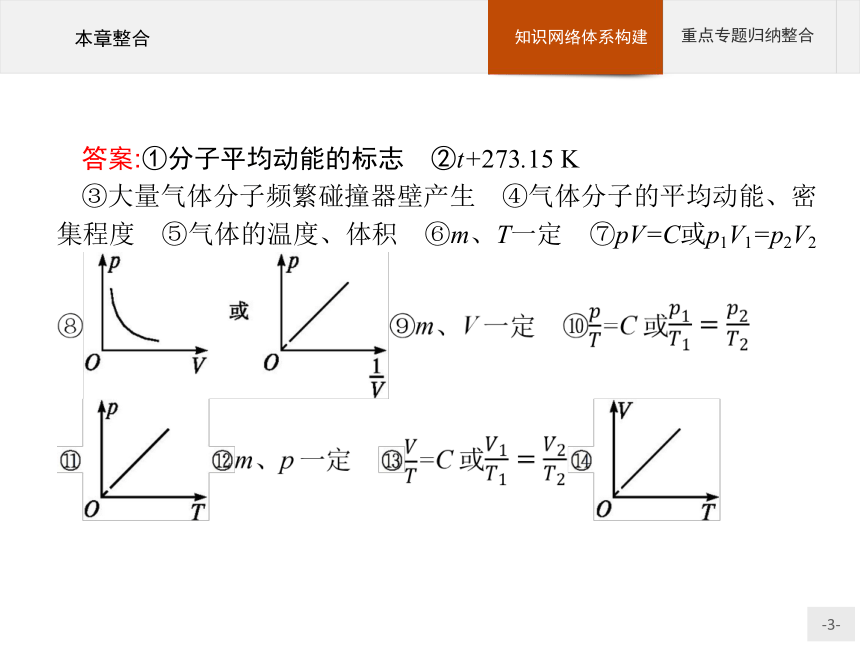
答案:①分子平均动能的标志 ②t+273.15
K
③大量气体分子频繁碰撞器壁产生 ④气体分子的平均动能、密集程度 ⑤气体的温度、体积 ⑥m、T一定 ⑦pV=C或p1V1=p2V2
2.气体的三个状态参量之间有何关系?
答案:三个状态参量是相互联系的,不是相互独立的。如温度、体积、压强这三个状态参量都保持不变,就是说气体处于一定的状态,气体的状态变化时,由
(C是恒量)知,至少有两个或三个参量同时改变。
3.思考“气体热现象的微观意义”一节学习的内容,正确填写下图
答案:①气体会充满它所能达到的空间,同一时间向各个方向运动的分子数目都相等;分子无规则运动,速率有大有小;速率分布为“中间多、两头少”
②温度是分子平均动能的标志
③气体压强是大量分子频繁撞击容器壁产生的
4.从微观和能量的角度如何正确认识理想气体?
答案:从微观上说,分子间以及分子和器壁间,除了碰撞外无其他作用力,分子本身没有体积,即它所占据的空间被认为都是可以被压缩的空间。
从能量角度上看,理想气体的微观本质是忽略了其分子力,所以其状态无论怎么变化都没有分子力做功,即没有分子势能的变化,于是理想气体的内能只有分子动能,即一定质量的理想气体的内能完全由温度决定。
专题一
专题二
专题一 封闭气体压强的计算
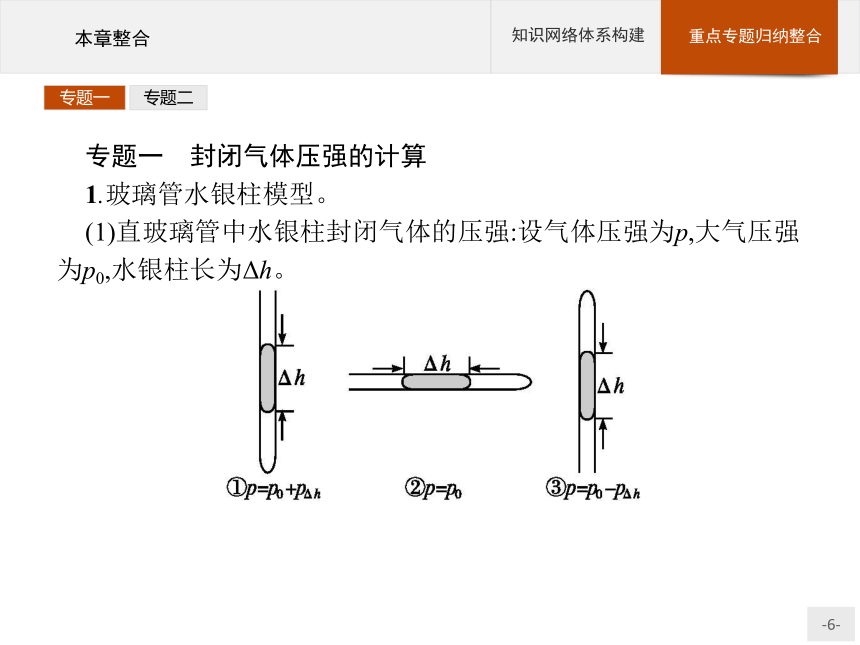
1.玻璃管水银柱模型。
(1)直玻璃管中水银柱封闭气体的压强:设气体压强为p,大气压强为p0,水银柱长为Δh。
专题一
专题二
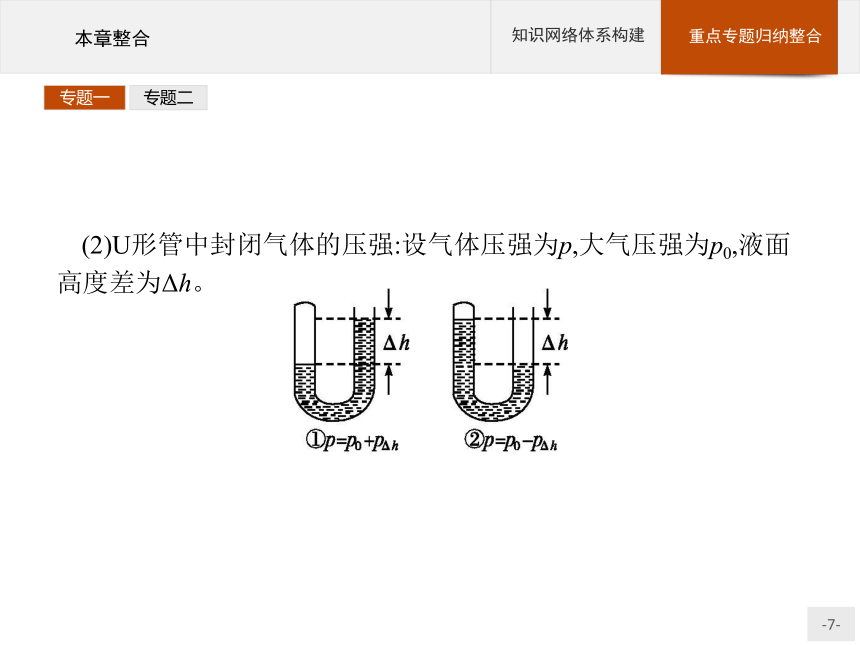
(2)U形管中封闭气体的压强:设气体压强为p,大气压强为p0,液面高度差为Δh。
专题一
专题二
2.汽缸活塞模型:设活塞质量为m,重力加速度为g,活塞面积为S,汽缸质量为m0,汽缸内气体压强为p,大气压强为p0。
专题一
专题二
【例题1】
在如图所示的汽缸中封闭着温度为127
℃的空气,一质量为m1的重物用绳索经滑轮与质量为m2的缸中活塞相连接,汽缸截面积为S,大气压为p0,重物和活塞均处于平衡状态,这时活塞离缸底的高度为10
cm,不计一切摩擦。
(1)求汽缸中封闭气体的压强;
(2)如果缸内空气温度缓慢下降,问:
①缸中封闭气体的压强是否改变?
②缸内空气变为27
℃时,重物从原处移动了多少厘米?
专题一
专题二
解析:(1)对活塞受力分析可得:m2g+p0S=pS+m1g
(2)①缸内空气温度缓慢下降时,缸外大气压强及重物对气体的压强不变,所以封闭气体的压强不变。
②缸内气体做等压变化,则气体初态体积V1=10
cm×S,温度T1=400
K,末态温度T2=300
K,体积设为V2=hS(h为活塞到缸底的距离)。据
可得h=7.5
cm,则重物从原处向上移动了2.5
cm。
专题一
专题二
变式训练1如图所示,两端开口的弯折的玻璃管竖直放置,两段竖直管内各有一段水银柱,两段空气封闭在三段水银柱之间,若左、右两管内水银柱长度分别为h1、h2,且水银柱均静止,则中间管内水银柱的长度为( )
解析:设大气压强为p0,左边空气的压强p左=p0-h1,右边空气的压强p右=p0+h2=p左+h,则h=h1+h2,故D正确。
答案:D
专题一
专题二
专题二 变质量问题转化为定质量问题的方法
分析气体的变质量问题时,可以通过巧妙地选择合适的研究对象,使这类问题转化为一定质量的气体问题,用相关规律求解。
1.充气问题。
向球、轮胎等封闭容器中充气是一个典型的变质量的气体问题。只要选择封闭容器内原有气体和即将充入的气体作为研究对象,就可把充气过程中的气体质量变化的问题转化为定质量的问题。
2.抽气问题。
从容器内抽气的过程中,容器内的气体质量不断减小,这属于变质量问题。分析时,将每次抽气过程中抽出的气体和剩余气体作为研究对象,可把抽气过程中的气体质量变化转化为定质量问题。
专题一
专题二
3.分装问题。
将一个大容器里的气体分装到多个小容器中的问题也是一个典型的变质量问题。分析这类问题时,可以把大容器中的剩余气体和多个小容器中的气体看成整体来作为研究对象,可将变质量问题转化为定质量问题。
4.漏气问题。
容器漏气过程中气体的质量不断发生变化,属于变质量问题,不能直接用相关方程求解。如果选容器内剩余气体为研究对象,便可使问题变成一定质量的气体状态变化,用相关方程求解。
专题一
专题二
【例题2】
如图所示,某压缩式喷雾器储液桶的容量是5.7×10-3
m3,往桶内倒入4.2×10-3
m3的药液后开始打气,打气过程中药液不会向外喷出。如果每次能打进体积为2.5×10-4
m3、压强为100
kPa的空气。
(1)要使喷雾器内空气的压强达到400
kPa,应打气几次?
(2)通过计算说明这个压强能否使喷雾器内的药液全部喷完?
专题一
专题二
解析:(1)设标准大气压为p0,药桶中空气的体积为V,打气N次后,喷雾器中的空气压强达到400
kPa,则打入的气体在标准大气压下的体积为V0N。
根据玻意耳定律p0(V+V0N)=4p0V
其中V=5.7×10-3
m3-4.2×10-3
m3=1.5×10-3
m3
代入数值后解得N=18。
(2)若空气完全充满药桶,由玻意耳定律有4p0V=p1V1,V1=5.7×10-3
m3
解得p1=1.053p0>p0
可见,药液可以全部喷完。
答案:(1)18次
(2)这个压强能使喷雾器内的药液全部喷完
专题一
专题二
变式训练2一只两用活塞气筒的原理如图所示(打气时如图甲,抽气时如图乙),其筒内体积为V0,现将它与另一只容积为V的容器相连接,气筒和容器内的空气压强为p0,已知气筒和容器导热性能良好,当分别作为打气筒和抽气筒时,活塞工作n次后,在上述两种情况下,容器内的气体压强分别为多少?
专题一
专题二
解析:打气时,活塞每推动一次,把体积为V0、压强为p0的气体推入容器内,若活塞工作n次,就是把压强为p0、体积为nV0的气体推入容器内、容器内原来有压强为p0、体积为V的气体,现在全部充入容器中,根据玻意耳定律得:p0(V+nV0)=p'V
抽气时,活塞每拉动一次,把容器中的气体的体积从V膨胀为V+V0,而容器中的气体压强就要减小,将抽气筒中的V0气体排出,而再次拉动活塞时,将容器中剩余的气体从V又膨胀到V+V0,容器内的压强继续减小,根据玻意耳定律得:
专题一
专题二
第八章 气体整合
思考并回答下列问题
本章知识可分为两个单元。第一单元,气体实验三定律,包括玻意耳定律、查理定律和盖—吕萨克定律;第二单元:理想气体状态方程和气体热现象的微观意义。
1.思考关于气体实验三定律学习的内容。正确填写下图
答案:①分子平均动能的标志 ②t+273.15
K
③大量气体分子频繁碰撞器壁产生 ④气体分子的平均动能、密集程度 ⑤气体的温度、体积 ⑥m、T一定 ⑦pV=C或p1V1=p2V2
2.气体的三个状态参量之间有何关系?
答案:三个状态参量是相互联系的,不是相互独立的。如温度、体积、压强这三个状态参量都保持不变,就是说气体处于一定的状态,气体的状态变化时,由
(C是恒量)知,至少有两个或三个参量同时改变。
3.思考“气体热现象的微观意义”一节学习的内容,正确填写下图
答案:①气体会充满它所能达到的空间,同一时间向各个方向运动的分子数目都相等;分子无规则运动,速率有大有小;速率分布为“中间多、两头少”
②温度是分子平均动能的标志
③气体压强是大量分子频繁撞击容器壁产生的
4.从微观和能量的角度如何正确认识理想气体?
答案:从微观上说,分子间以及分子和器壁间,除了碰撞外无其他作用力,分子本身没有体积,即它所占据的空间被认为都是可以被压缩的空间。
从能量角度上看,理想气体的微观本质是忽略了其分子力,所以其状态无论怎么变化都没有分子力做功,即没有分子势能的变化,于是理想气体的内能只有分子动能,即一定质量的理想气体的内能完全由温度决定。
专题一
专题二
专题一 封闭气体压强的计算
1.玻璃管水银柱模型。
(1)直玻璃管中水银柱封闭气体的压强:设气体压强为p,大气压强为p0,水银柱长为Δh。
专题一
专题二
(2)U形管中封闭气体的压强:设气体压强为p,大气压强为p0,液面高度差为Δh。
专题一
专题二
2.汽缸活塞模型:设活塞质量为m,重力加速度为g,活塞面积为S,汽缸质量为m0,汽缸内气体压强为p,大气压强为p0。
专题一
专题二
【例题1】
在如图所示的汽缸中封闭着温度为127
℃的空气,一质量为m1的重物用绳索经滑轮与质量为m2的缸中活塞相连接,汽缸截面积为S,大气压为p0,重物和活塞均处于平衡状态,这时活塞离缸底的高度为10
cm,不计一切摩擦。
(1)求汽缸中封闭气体的压强;
(2)如果缸内空气温度缓慢下降,问:
①缸中封闭气体的压强是否改变?
②缸内空气变为27
℃时,重物从原处移动了多少厘米?
专题一
专题二
解析:(1)对活塞受力分析可得:m2g+p0S=pS+m1g
(2)①缸内空气温度缓慢下降时,缸外大气压强及重物对气体的压强不变,所以封闭气体的压强不变。
②缸内气体做等压变化,则气体初态体积V1=10
cm×S,温度T1=400
K,末态温度T2=300
K,体积设为V2=hS(h为活塞到缸底的距离)。据
可得h=7.5
cm,则重物从原处向上移动了2.5
cm。
专题一
专题二
变式训练1如图所示,两端开口的弯折的玻璃管竖直放置,两段竖直管内各有一段水银柱,两段空气封闭在三段水银柱之间,若左、右两管内水银柱长度分别为h1、h2,且水银柱均静止,则中间管内水银柱的长度为( )
解析:设大气压强为p0,左边空气的压强p左=p0-h1,右边空气的压强p右=p0+h2=p左+h,则h=h1+h2,故D正确。
答案:D
专题一
专题二
专题二 变质量问题转化为定质量问题的方法
分析气体的变质量问题时,可以通过巧妙地选择合适的研究对象,使这类问题转化为一定质量的气体问题,用相关规律求解。
1.充气问题。
向球、轮胎等封闭容器中充气是一个典型的变质量的气体问题。只要选择封闭容器内原有气体和即将充入的气体作为研究对象,就可把充气过程中的气体质量变化的问题转化为定质量的问题。
2.抽气问题。
从容器内抽气的过程中,容器内的气体质量不断减小,这属于变质量问题。分析时,将每次抽气过程中抽出的气体和剩余气体作为研究对象,可把抽气过程中的气体质量变化转化为定质量问题。
专题一
专题二
3.分装问题。
将一个大容器里的气体分装到多个小容器中的问题也是一个典型的变质量问题。分析这类问题时,可以把大容器中的剩余气体和多个小容器中的气体看成整体来作为研究对象,可将变质量问题转化为定质量问题。
4.漏气问题。
容器漏气过程中气体的质量不断发生变化,属于变质量问题,不能直接用相关方程求解。如果选容器内剩余气体为研究对象,便可使问题变成一定质量的气体状态变化,用相关方程求解。
专题一
专题二
【例题2】
如图所示,某压缩式喷雾器储液桶的容量是5.7×10-3
m3,往桶内倒入4.2×10-3
m3的药液后开始打气,打气过程中药液不会向外喷出。如果每次能打进体积为2.5×10-4
m3、压强为100
kPa的空气。
(1)要使喷雾器内空气的压强达到400
kPa,应打气几次?
(2)通过计算说明这个压强能否使喷雾器内的药液全部喷完?
专题一
专题二
解析:(1)设标准大气压为p0,药桶中空气的体积为V,打气N次后,喷雾器中的空气压强达到400
kPa,则打入的气体在标准大气压下的体积为V0N。
根据玻意耳定律p0(V+V0N)=4p0V
其中V=5.7×10-3
m3-4.2×10-3
m3=1.5×10-3
m3
代入数值后解得N=18。
(2)若空气完全充满药桶,由玻意耳定律有4p0V=p1V1,V1=5.7×10-3
m3
解得p1=1.053p0>p0
可见,药液可以全部喷完。
答案:(1)18次
(2)这个压强能使喷雾器内的药液全部喷完
专题一
专题二
变式训练2一只两用活塞气筒的原理如图所示(打气时如图甲,抽气时如图乙),其筒内体积为V0,现将它与另一只容积为V的容器相连接,气筒和容器内的空气压强为p0,已知气筒和容器导热性能良好,当分别作为打气筒和抽气筒时,活塞工作n次后,在上述两种情况下,容器内的气体压强分别为多少?
专题一
专题二
解析:打气时,活塞每推动一次,把体积为V0、压强为p0的气体推入容器内,若活塞工作n次,就是把压强为p0、体积为nV0的气体推入容器内、容器内原来有压强为p0、体积为V的气体,现在全部充入容器中,根据玻意耳定律得:p0(V+nV0)=p'V
抽气时,活塞每拉动一次,把容器中的气体的体积从V膨胀为V+V0,而容器中的气体压强就要减小,将抽气筒中的V0气体排出,而再次拉动活塞时,将容器中剩余的气体从V又膨胀到V+V0,容器内的压强继续减小,根据玻意耳定律得:
专题一
专题二
