华东师大版数学八年级下册课件: 19.1.1矩形的性质 (30张PPT)
文档属性
| 名称 | 华东师大版数学八年级下册课件: 19.1.1矩形的性质 (30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-04 23:08:57 | ||
图片预览






文档简介
(共30张PPT)
19.1.1矩形的性质
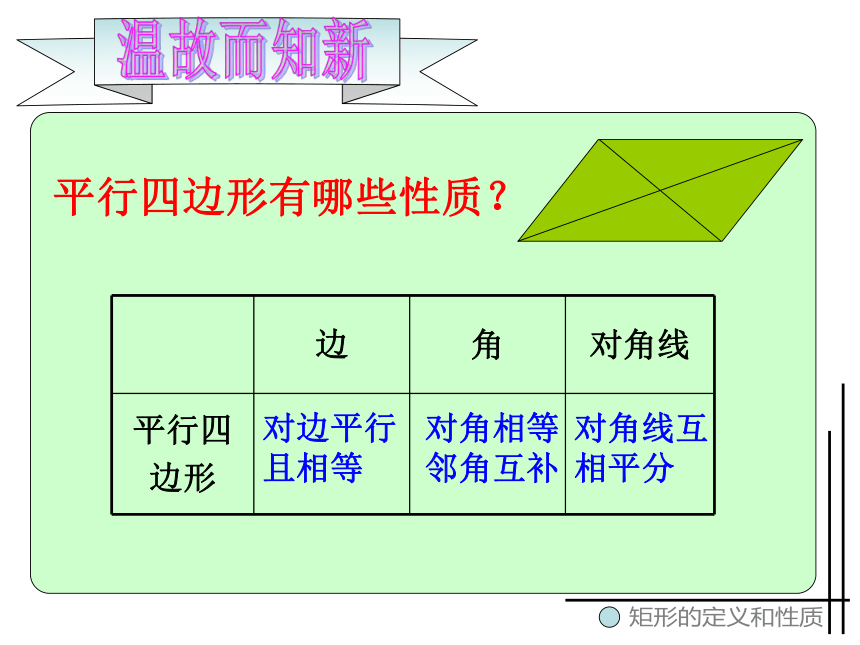
平行四边形有哪些性质?
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
边
角
对角线
平行四
边形
两组对边
分别平行
我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说也有特殊情况,这堂课我们就来研究一种特殊的平行四边形——
矩形
细心观察平行四边形内角的变化
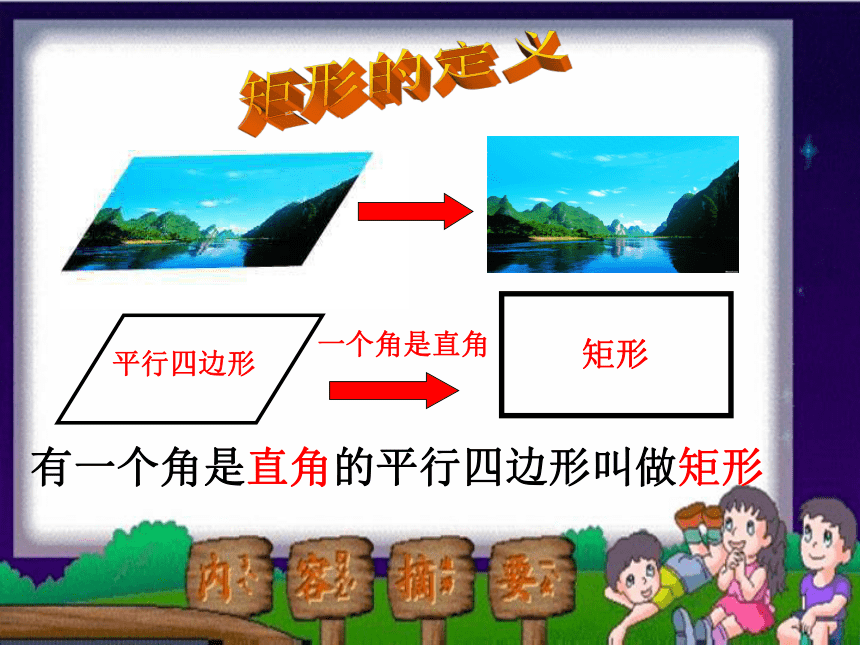
一个角是直角
有一个角是直角的平行四边形叫做矩形
矩形
平行四边形
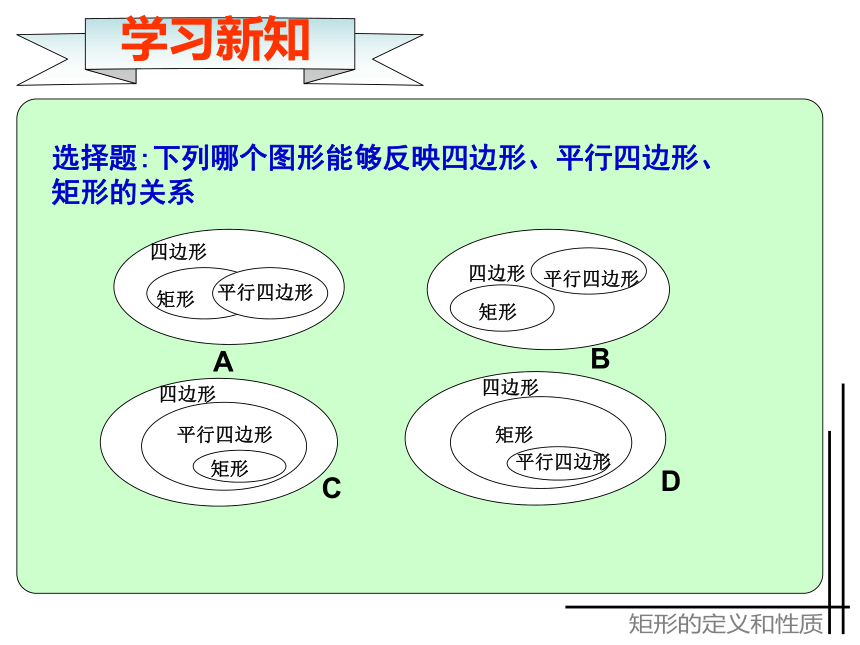
选择题:下列哪个图形能够反映四边形、平行四边形、
矩形的关系
学习新知
矩形的性质的研究
我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有其它的特殊性质.你能说出矩形有哪些特殊性质吗?
四、矩形
两条对角线互相平分
三、矩形的两组对角分别相等
二、矩形的两组对边分别相等
一、矩形的两组对边分别平行
五、矩形的邻角互补
请同学们用量角器度量你的课本每个角的度数,用直尺度量两条对角线的长度.并且根据你得到的数据提出你的猜想.
要大胆,不要拘束
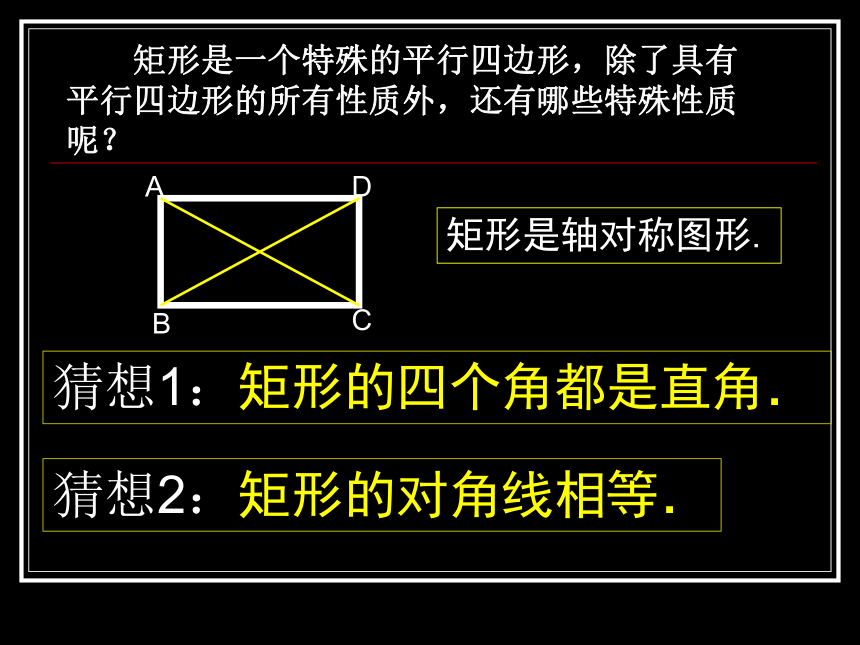
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
矩形是轴对称图形.
A
B
C
D
1:矩形的四个角都是直角
已知:四边形ABCD是矩形,
∠B=90°
求证:∠A=∠B=∠C=∠D=90°
D
C
B
A
证明:∵四边形ABCD是平行四边形,
∠B=90°
∴∠B=∠D=90°
∠B+∠C=180
°
∴∠B+
∠
A=180°
∴∠A=∠B=∠C=∠D=90°
性质
命题
已知:四边形ABCD是矩形,求证:AC
=
BD
证明:在矩形ABCD中
∵∠ABC
=
∠DCB
=
90°
又∵AB
=
DC
,
BC
=
CB
∴△ABC≌△DCB
∴AC
=
BD
2:矩形的对角线相等.
性质
命题
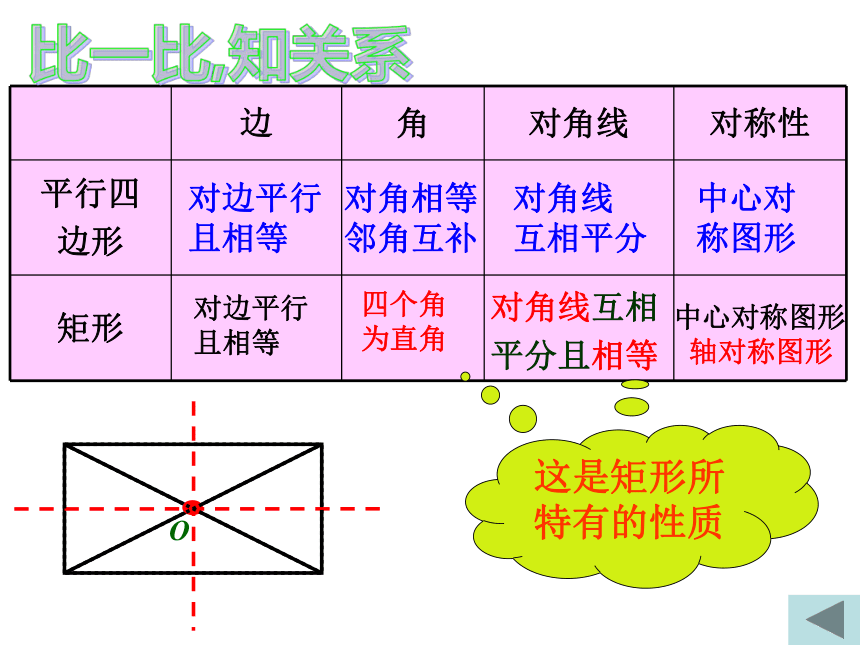
对边平行
且相等
对角相等
邻角互补
对角线
互相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
O
边
角
对角线
对称性
平行四
边形
矩形
矩形的
两条对角线互相平分
矩形的两组对边分别平行
矩形的两组对边分别相等
矩形的四个角都是直角
矩形
的两条对角线相等
边
对角线
角
数学语言
∵四边形ABCD是矩形
∴AD
=
BC
,CD
=
AB
∴AD
∥BC
,CD
∥AB
∴AC=
BD
∴AO=
CO
,OD
=
OB
O
D
C
B
A
相等的线段:
相等的角:
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC
∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD
∠OAD=∠ODA=∠OBC=∠OCB
等腰三角形有:
△OAB
△
OBC
△OCD
△OAD
直角三角形有:
Rt△ABC
Rt△BCD
Rt△CDA
Rt△DAB
全等三角形有:
Rt△ABC
≌
Rt△BCD
≌
Rt△CDA
≌
Rt△DAB
△OAB≌△OCD
△OAD≌△OCB
已知四边形ABCD是矩形
O
A
B
C
D
公平,因为OA=OC=OB=OD
O
D
C
B
A
┛
在Rt△ABD中,AO是斜边BD的中线
直角三角形的性质:直角三角形斜边
上的中线等于斜边的一半。
则有:OA=
OB=OD=
BD
已知
如图:
△ABC是Rt△,∠ABC=Rt∠,
BD是斜边AC上的中线
若BD=3㎝,则AC=
㎝
2
若∠C=30°,AB=5㎝,则AC=
㎝,
BD=
㎝,∠BDC=
3
判断△ABD形状:
判断△CBD形状:
6
5
10
120°
等腰三角形
等腰三角形
例1
已知:矩形ABCD的两条对角线相交与O,∠AOD=120°,AB
=
4cm.
求矩形对角线的长
∴BD
=
2AB=2×4=8cm
解:∵四边形ABCD是矩形
∴OA
=
OD(
)
∵
∠AOD=120°
∴
∠1=30°
又∵
∠ABC=90°(
)
矩形的对角线相等且平分
矩形的每个内角都是直角
例2:如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线的长是13cm,那么矩形的周长是多少?
在矩形ABCD中,有
AD=BC;AB=CD;AC=DB;
AO=OC=OB=OD
∴AD+BC+AB+DC+2AC+2BD=86
又∵AC=DB=13
∴AD+AB+BC+DC=86-52=34
本节课我的收获是
。
老师对数学学习建议:
乐于探究、主动参与、学会自学是你学好数学的保证;
善于把已有的知识做为获得新知的桥梁是你学好数学的关键。
(1)矩形具有而平行四边形不具有的性质(
)
(A)内角和是360度
(B)对角相等
(C)对边平行且相等
(D)对角线相等
(2)下面性质中,矩形不一定具有的是(
)
(A)对角线相等
(B)四个角相等
(C)是轴对称图形
(D)对角线垂直
(3)
已知矩形的一条对角线与一边的夹角是40°,
则两条对角线所夹锐角的度数为
(
)
(A)50°
(B)60°
(C)70°
(D)80°
D
第一关
D
D
第一关
如图:四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC=
㎝
OB=
㎝
DE=
㎝
若已知∠CAB=40°,则∠OCB=
∠OBA=
∠AOB=
∠AOD=
若已知AC=10㎝,BC=6㎝,则矩形的周长=
㎝
矩形的面积=
㎝2
4
若已知
∠DOC=120°,AD=6㎝,则AC=
㎝
5
50°
10
100°
40°
12
48
28
80°
第二关
E
□
4.8
第二关
矩形的四个角都是直角.
※
矩形的性质1
矩形的对角线相等.
※
矩形的性质2
※
推
论
直角三角形斜边上的中线等于斜边的一半.
2、
如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
解:
∵
△AOB、
△BOC、
△COD
和△AOD四个三角形的周长和为86cm,
又∵
AC=BD=13cm,
∴
AB+BC+CD+DA=86-2(AC+BD)
=86-4×13=34(cm)
即矩形ABCD的周长等于34cm。
O
思考题
如图,在△ABC中,D,E,F,分别是BC、AC、AB边的中点,AH⊥BC于H,FD=8㎝,则HE=
8㎝
小试身手
1.为了庆祝五一劳动节,新民学校八年级(13)班同学要在广场上布置一个矩形的花坛,计划用“串红”摆成两条对角线,如果一条对角线用了38盆“串红”,还需要从花房里运来多少盆“串红”?为什么?如果一条对角线用了49盆呢?为什么?
生活链接
2.如图,用8块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别是(
)
(A)48cm,12cm;
(B)48cm,16cm;
(C)44cm,16cm;
(D)45cm,15cm.
D
直角三角形性质
直角三角形斜边上的中线等于斜边的一半
推论
解题指导:矩形问题
直角三角形或等腰三角形
连接对角线
转化
已知:在△ABC中∠ACB=90°,AD
=
BD
证明:延长CD到E使DE=CD,连
结AE、BE.
∵AD
=
BD
,CD
=
ED
E
∴ACBE是平行四边形
又∵∠ACB
=
90
∴CE
=
AB
芳草的哭泣:新民学校在建设绿色校园的过程中修建了一块长8米,宽6米的矩形绿草地,为方便师生参观,沿对角线修筑了一条卵石小道.但是……唉!
8米
6米
例:
如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?
解:∵
四边形ABCD是矩形
∴AC与BD相等且互相平分
∴
OA=OB
∵
∠AOB=60°
∴
△AOB是等边三角形
∴
OA=AB=4(㎝)
∴
矩形的对角线长
AC=BD=2OA=8(㎝)
O
已知对角线长是8cm,两对角线的一个夹角∠AOD是120°,
求矩形的长BC与宽AB.
变式:
方法小结:如果矩形两对角
线的夹角是60°或120°,
则其中必有等边三角形.
19.1.1矩形的性质
平行四边形有哪些性质?
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
边
角
对角线
平行四
边形
两组对边
分别平行
我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说也有特殊情况,这堂课我们就来研究一种特殊的平行四边形——
矩形
细心观察平行四边形内角的变化
一个角是直角
有一个角是直角的平行四边形叫做矩形
矩形
平行四边形
选择题:下列哪个图形能够反映四边形、平行四边形、
矩形的关系
学习新知
矩形的性质的研究
我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有其它的特殊性质.你能说出矩形有哪些特殊性质吗?
四、矩形
两条对角线互相平分
三、矩形的两组对角分别相等
二、矩形的两组对边分别相等
一、矩形的两组对边分别平行
五、矩形的邻角互补
请同学们用量角器度量你的课本每个角的度数,用直尺度量两条对角线的长度.并且根据你得到的数据提出你的猜想.
要大胆,不要拘束
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
矩形是轴对称图形.
A
B
C
D
1:矩形的四个角都是直角
已知:四边形ABCD是矩形,
∠B=90°
求证:∠A=∠B=∠C=∠D=90°
D
C
B
A
证明:∵四边形ABCD是平行四边形,
∠B=90°
∴∠B=∠D=90°
∠B+∠C=180
°
∴∠B+
∠
A=180°
∴∠A=∠B=∠C=∠D=90°
性质
命题
已知:四边形ABCD是矩形,求证:AC
=
BD
证明:在矩形ABCD中
∵∠ABC
=
∠DCB
=
90°
又∵AB
=
DC
,
BC
=
CB
∴△ABC≌△DCB
∴AC
=
BD
2:矩形的对角线相等.
性质
命题
对边平行
且相等
对角相等
邻角互补
对角线
互相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
O
边
角
对角线
对称性
平行四
边形
矩形
矩形的
两条对角线互相平分
矩形的两组对边分别平行
矩形的两组对边分别相等
矩形的四个角都是直角
矩形
的两条对角线相等
边
对角线
角
数学语言
∵四边形ABCD是矩形
∴AD
=
BC
,CD
=
AB
∴AD
∥BC
,CD
∥AB
∴AC=
BD
∴AO=
CO
,OD
=
OB
O
D
C
B
A
相等的线段:
相等的角:
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC
∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD
∠OAD=∠ODA=∠OBC=∠OCB
等腰三角形有:
△OAB
△
OBC
△OCD
△OAD
直角三角形有:
Rt△ABC
Rt△BCD
Rt△CDA
Rt△DAB
全等三角形有:
Rt△ABC
≌
Rt△BCD
≌
Rt△CDA
≌
Rt△DAB
△OAB≌△OCD
△OAD≌△OCB
已知四边形ABCD是矩形
O
A
B
C
D
公平,因为OA=OC=OB=OD
O
D
C
B
A
┛
在Rt△ABD中,AO是斜边BD的中线
直角三角形的性质:直角三角形斜边
上的中线等于斜边的一半。
则有:OA=
OB=OD=
BD
已知
如图:
△ABC是Rt△,∠ABC=Rt∠,
BD是斜边AC上的中线
若BD=3㎝,则AC=
㎝
2
若∠C=30°,AB=5㎝,则AC=
㎝,
BD=
㎝,∠BDC=
3
判断△ABD形状:
判断△CBD形状:
6
5
10
120°
等腰三角形
等腰三角形
例1
已知:矩形ABCD的两条对角线相交与O,∠AOD=120°,AB
=
4cm.
求矩形对角线的长
∴BD
=
2AB=2×4=8cm
解:∵四边形ABCD是矩形
∴OA
=
OD(
)
∵
∠AOD=120°
∴
∠1=30°
又∵
∠ABC=90°(
)
矩形的对角线相等且平分
矩形的每个内角都是直角
例2:如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线的长是13cm,那么矩形的周长是多少?
在矩形ABCD中,有
AD=BC;AB=CD;AC=DB;
AO=OC=OB=OD
∴AD+BC+AB+DC+2AC+2BD=86
又∵AC=DB=13
∴AD+AB+BC+DC=86-52=34
本节课我的收获是
。
老师对数学学习建议:
乐于探究、主动参与、学会自学是你学好数学的保证;
善于把已有的知识做为获得新知的桥梁是你学好数学的关键。
(1)矩形具有而平行四边形不具有的性质(
)
(A)内角和是360度
(B)对角相等
(C)对边平行且相等
(D)对角线相等
(2)下面性质中,矩形不一定具有的是(
)
(A)对角线相等
(B)四个角相等
(C)是轴对称图形
(D)对角线垂直
(3)
已知矩形的一条对角线与一边的夹角是40°,
则两条对角线所夹锐角的度数为
(
)
(A)50°
(B)60°
(C)70°
(D)80°
D
第一关
D
D
第一关
如图:四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC=
㎝
OB=
㎝
DE=
㎝
若已知∠CAB=40°,则∠OCB=
∠OBA=
∠AOB=
∠AOD=
若已知AC=10㎝,BC=6㎝,则矩形的周长=
㎝
矩形的面积=
㎝2
4
若已知
∠DOC=120°,AD=6㎝,则AC=
㎝
5
50°
10
100°
40°
12
48
28
80°
第二关
E
□
4.8
第二关
矩形的四个角都是直角.
※
矩形的性质1
矩形的对角线相等.
※
矩形的性质2
※
推
论
直角三角形斜边上的中线等于斜边的一半.
2、
如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
解:
∵
△AOB、
△BOC、
△COD
和△AOD四个三角形的周长和为86cm,
又∵
AC=BD=13cm,
∴
AB+BC+CD+DA=86-2(AC+BD)
=86-4×13=34(cm)
即矩形ABCD的周长等于34cm。
O
思考题
如图,在△ABC中,D,E,F,分别是BC、AC、AB边的中点,AH⊥BC于H,FD=8㎝,则HE=
8㎝
小试身手
1.为了庆祝五一劳动节,新民学校八年级(13)班同学要在广场上布置一个矩形的花坛,计划用“串红”摆成两条对角线,如果一条对角线用了38盆“串红”,还需要从花房里运来多少盆“串红”?为什么?如果一条对角线用了49盆呢?为什么?
生活链接
2.如图,用8块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别是(
)
(A)48cm,12cm;
(B)48cm,16cm;
(C)44cm,16cm;
(D)45cm,15cm.
D
直角三角形性质
直角三角形斜边上的中线等于斜边的一半
推论
解题指导:矩形问题
直角三角形或等腰三角形
连接对角线
转化
已知:在△ABC中∠ACB=90°,AD
=
BD
证明:延长CD到E使DE=CD,连
结AE、BE.
∵AD
=
BD
,CD
=
ED
E
∴ACBE是平行四边形
又∵∠ACB
=
90
∴CE
=
AB
芳草的哭泣:新民学校在建设绿色校园的过程中修建了一块长8米,宽6米的矩形绿草地,为方便师生参观,沿对角线修筑了一条卵石小道.但是……唉!
8米
6米
例:
如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?
解:∵
四边形ABCD是矩形
∴AC与BD相等且互相平分
∴
OA=OB
∵
∠AOB=60°
∴
△AOB是等边三角形
∴
OA=AB=4(㎝)
∴
矩形的对角线长
AC=BD=2OA=8(㎝)
O
已知对角线长是8cm,两对角线的一个夹角∠AOD是120°,
求矩形的长BC与宽AB.
变式:
方法小结:如果矩形两对角
线的夹角是60°或120°,
则其中必有等边三角形.
