人教版七年级数学下册 9.2 一元一次不等式课件 (共31张PPT )
文档属性
| 名称 | 人教版七年级数学下册 9.2 一元一次不等式课件 (共31张PPT ) |

|
|
| 格式 | zip | ||
| 文件大小 | 816.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-03 22:00:51 | ||
图片预览



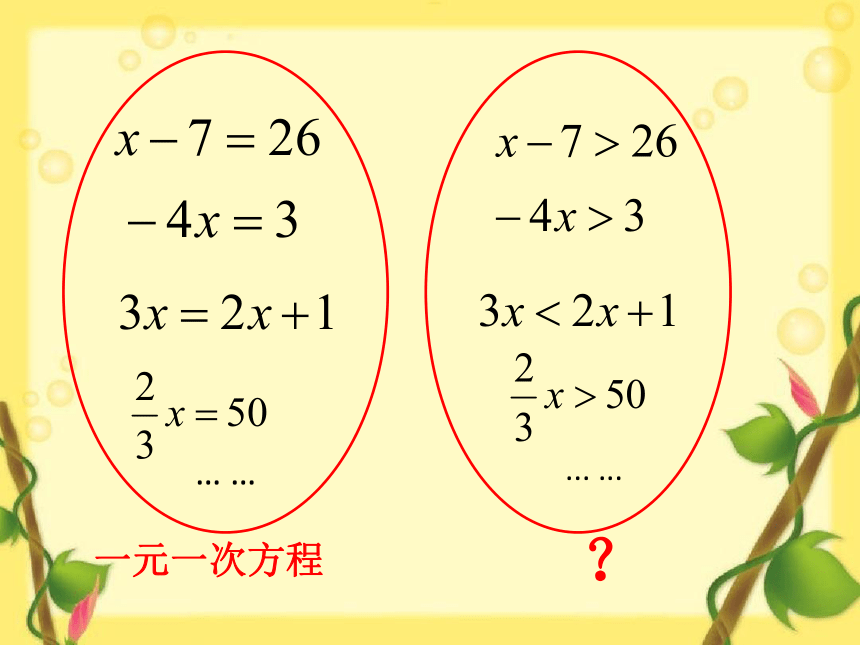








文档简介
(共31张PPT)
9:20开始上课,请同学们提前做好以下准备:
课本122页、9.2.1导学案;
练习本;
红、黑双色笔;
4.其它无关用品收起来.
不等式的性质1
不等式两边加或减同一个数(或式子),不等号的方向不变.
不等式的性质2
不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式的性质3
不等式两边乘(或除以)同一个负数,不等号的方向改变.
什么叫一元一次方程
?
只含一个未知数(元),并且未知数的次数都是1,等号两边都是整式的方程叫做一元一次方程。
一元一次方程
?
…
…
...
...
第九章
不等式与不等式组
9.2
一元一次不等式
第1课时
一元一次不等式的解法
1.理解和掌握一元一次不等式的概念;
2.会用不等式的性质熟练地解一元一次不等式.(重点、
难点)
学习目标
问题1 观察下面的式子,它们有哪些共同特征?
1.
引入概念
?都是不等式
?只含有一个未知数
?未知数的次数是1
?不等号两边都是整式
只含有一个未知数,且未知数的次数是1的不等式,称为一元一次不等式.
它与一元一次方程的定义有什么共同点吗?
一元一次不等式的概念
?
判断下列不等式是不是一元一次不等式?
(1)
(2)
(3)
(4)
?
?
(5)
(6)
√
√
?
例1
已知
是关于x的一元一次不等式,
则a的值是________.
解析:由
是关于x的一元一次不等式得2a-1=1,计算即可求出a的值等于1.
1
练习
利用不等式的性质求不等式解集:
解:根据不等式的性质1,不等式的两边减3,
不等号的方向不变,所以
2.
研究解法
xx
+<3
<
10
x<10
-
3
-3
x
+
3
-
3
<
10
-
3
1.方程中的移项法则在不等式中仍然适用
x<<,10
-
3
+3
2.移项要变号,不等号方向不变;
解:
移项得 x
<10-3
即
x
<
7
这个不等式的解集在数轴上表示如下:
0
实心点和空心圆分别在什么时候适用?
7
一元一次方程的解法
探究
去分母
去括号
移项
合并同类项
系数化为1
一元一次不等式的解法
解下列不等式,并把它的解集表示在数轴上
探究
解:
0
4
去分母
去括号
移项
合并同类项
系数化为1
不等式的性质2
不等式的性质1
不等式的性质3
注意不等号的方向要改变
解一元一次不等式与解一元一次方程的依据和步骤有什么异同点?
它们的依据不相同.解一元一次方程的依据是等式的性质,解一元一次不等式的依据是不等式的性质.
它们的步骤基本相同,都是去分母、去括号、移项、合并同类项、未知数的系数化为1.
这些步骤中,要特别注意的是:不等式两边都乘(或除以)同一个负数,必须改变不等号的方向.这是与解一元一次方程不同的地方.
议一议
例2 解下列不等式,并在数轴上表示解集:
移项,得
合并同类项,得
系数化为1,得
解:去括号,得
2x<3-2
0
不等式的解集在数轴上表示为:
例2 解下列不等式,并在数轴上表示解集:
去括号,得
移项,得
合并同类项,得
系数化为1,得
0
8
解:去分母,得
不等式的解集在数轴上表示为:
解下列不等式,并在数轴上表示其解集.
(1)
(4)
(3)
(2)
巩固练习
解下列不等式,并在数轴上表示其解集.
(1)
(2)
在数轴上表示其解集为:
解:
解:
在数轴上表示其解集为:
巩固练习
巩固练习
解下列不等式,并在数轴上表示其解集.
(4)
(3)
解:
解:
在数轴上表示其解集为:
在数轴上表示其解集为:
解:由方程的解的定义,把x=3代入ax+12=0中,
得
a=-4.
把a=-4代入(a+2)x>-6中,
得-2x>-6,
解得x<3.
在数轴上表示如图:
其中正整数解有1和2.
例3
已知方程ax+12=0的解是x=3,求关于x不等式
(a+2)x>-6的解集,并在数轴上表示出来,其
中正整数解有哪些?
-1
0
1
2
3
4
5
6
求不等式的特殊解,先要准确求出不等式的解集,然后确定特殊解.在确定特殊解时,一定要注意是否包括端点的值,一般可以结合数轴,形象直观,一目了然.
方法总结
解
解得
x
≤
6.
x≤6在数轴上表示为:
-1
0
1
2
3
4
5
6
根据题意,得
x
+2≥
0,
所以,当x≤6时,代数式
x+2的值是非负数.
满足条件的正整数有
1,2,3,4,5,6.
当x取什么值时,代数式
x
+2的值是非负数?并求出所有满足条件的正整数.
巩固练习
例4关于x的不等式
3x-2a
≤
-2的解集如图所示,求a的值.
-1
0
1
解:移项,得
系数化为1,得
3x
≤
2a-2
由图可知:
x
≤
-1
所以
解这个方程,得
方法总结:
已知解集求字母系数的值,通常是先解含有字母的不等式,再利用解集的唯一性列方程求字母的值.
巩固练习
根据下列条件,分别求出a的值或取值范围:
(1)已知不等式
的解集是x<5;
(2)已知x=5是不等式
的解.
解:
(1)2x-4>3x+a
2x-3x>a+4
-x>(a+4)
∴解集是:x<-a-4
∵解集是x<5
∴-a-4=5
a=
-9
(2)据题意有:
即6>15+a
解得:a<-9
注意:变号!
当堂检测
1.一个两位数,十位数字与个位数字的和为6,且这个两位数不大于42,则这样的两位数有
个.
4
当堂检测
1.一个两位数,十位数字与个位数字的和为6,且这个两位数不大于42,则这样的两位数有
个.
2.能使不等式
成立的x的最大整数
是
.
4
-1
当堂检测
1.一个两位数,十位数字与个位数字的和为6,且这个两位数不大于42,则这样的两位数有
个.
2.能使不等式
成立的x的最大整数
是
.
3.不等式
的解集是
则m的值为_________
4
-1
4
课堂小结
解一元一次不等式的步骤:
1.去分母
2.去括号
3.
移项
4.
合并同类项
5.
系数化为
1
注意:利用不等式的性质3,不等式两边同乘或除以负数时,不等号方向改变.
一元一次不等式定义:
只含有一个未知数,且未知数的次数是1的不等式
1.订正9.2.1一元一次不等式(1)导学案;
2.完成9.2.1一元一次不等式(1)自助餐;
3.预习课本P124-125;
4.完成9.2.1一元一次不等式(2)导学案.
布置作业
9:20开始上课,请同学们提前做好以下准备:
课本122页、9.2.1导学案;
练习本;
红、黑双色笔;
4.其它无关用品收起来.
不等式的性质1
不等式两边加或减同一个数(或式子),不等号的方向不变.
不等式的性质2
不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式的性质3
不等式两边乘(或除以)同一个负数,不等号的方向改变.
什么叫一元一次方程
?
只含一个未知数(元),并且未知数的次数都是1,等号两边都是整式的方程叫做一元一次方程。
一元一次方程
?
…
…
...
...
第九章
不等式与不等式组
9.2
一元一次不等式
第1课时
一元一次不等式的解法
1.理解和掌握一元一次不等式的概念;
2.会用不等式的性质熟练地解一元一次不等式.(重点、
难点)
学习目标
问题1 观察下面的式子,它们有哪些共同特征?
1.
引入概念
?都是不等式
?只含有一个未知数
?未知数的次数是1
?不等号两边都是整式
只含有一个未知数,且未知数的次数是1的不等式,称为一元一次不等式.
它与一元一次方程的定义有什么共同点吗?
一元一次不等式的概念
?
判断下列不等式是不是一元一次不等式?
(1)
(2)
(3)
(4)
?
?
(5)
(6)
√
√
?
例1
已知
是关于x的一元一次不等式,
则a的值是________.
解析:由
是关于x的一元一次不等式得2a-1=1,计算即可求出a的值等于1.
1
练习
利用不等式的性质求不等式解集:
解:根据不等式的性质1,不等式的两边减3,
不等号的方向不变,所以
2.
研究解法
xx
+<3
<
10
x<10
-
3
-3
x
+
3
-
3
<
10
-
3
1.方程中的移项法则在不等式中仍然适用
x<<,10
-
3
+3
2.移项要变号,不等号方向不变;
解:
移项得 x
<10-3
即
x
<
7
这个不等式的解集在数轴上表示如下:
0
实心点和空心圆分别在什么时候适用?
7
一元一次方程的解法
探究
去分母
去括号
移项
合并同类项
系数化为1
一元一次不等式的解法
解下列不等式,并把它的解集表示在数轴上
探究
解:
0
4
去分母
去括号
移项
合并同类项
系数化为1
不等式的性质2
不等式的性质1
不等式的性质3
注意不等号的方向要改变
解一元一次不等式与解一元一次方程的依据和步骤有什么异同点?
它们的依据不相同.解一元一次方程的依据是等式的性质,解一元一次不等式的依据是不等式的性质.
它们的步骤基本相同,都是去分母、去括号、移项、合并同类项、未知数的系数化为1.
这些步骤中,要特别注意的是:不等式两边都乘(或除以)同一个负数,必须改变不等号的方向.这是与解一元一次方程不同的地方.
议一议
例2 解下列不等式,并在数轴上表示解集:
移项,得
合并同类项,得
系数化为1,得
解:去括号,得
2x<3-2
0
不等式的解集在数轴上表示为:
例2 解下列不等式,并在数轴上表示解集:
去括号,得
移项,得
合并同类项,得
系数化为1,得
0
8
解:去分母,得
不等式的解集在数轴上表示为:
解下列不等式,并在数轴上表示其解集.
(1)
(4)
(3)
(2)
巩固练习
解下列不等式,并在数轴上表示其解集.
(1)
(2)
在数轴上表示其解集为:
解:
解:
在数轴上表示其解集为:
巩固练习
巩固练习
解下列不等式,并在数轴上表示其解集.
(4)
(3)
解:
解:
在数轴上表示其解集为:
在数轴上表示其解集为:
解:由方程的解的定义,把x=3代入ax+12=0中,
得
a=-4.
把a=-4代入(a+2)x>-6中,
得-2x>-6,
解得x<3.
在数轴上表示如图:
其中正整数解有1和2.
例3
已知方程ax+12=0的解是x=3,求关于x不等式
(a+2)x>-6的解集,并在数轴上表示出来,其
中正整数解有哪些?
-1
0
1
2
3
4
5
6
求不等式的特殊解,先要准确求出不等式的解集,然后确定特殊解.在确定特殊解时,一定要注意是否包括端点的值,一般可以结合数轴,形象直观,一目了然.
方法总结
解
解得
x
≤
6.
x≤6在数轴上表示为:
-1
0
1
2
3
4
5
6
根据题意,得
x
+2≥
0,
所以,当x≤6时,代数式
x+2的值是非负数.
满足条件的正整数有
1,2,3,4,5,6.
当x取什么值时,代数式
x
+2的值是非负数?并求出所有满足条件的正整数.
巩固练习
例4关于x的不等式
3x-2a
≤
-2的解集如图所示,求a的值.
-1
0
1
解:移项,得
系数化为1,得
3x
≤
2a-2
由图可知:
x
≤
-1
所以
解这个方程,得
方法总结:
已知解集求字母系数的值,通常是先解含有字母的不等式,再利用解集的唯一性列方程求字母的值.
巩固练习
根据下列条件,分别求出a的值或取值范围:
(1)已知不等式
的解集是x<5;
(2)已知x=5是不等式
的解.
解:
(1)2x-4>3x+a
2x-3x>a+4
-x>(a+4)
∴解集是:x<-a-4
∵解集是x<5
∴-a-4=5
a=
-9
(2)据题意有:
即6>15+a
解得:a<-9
注意:变号!
当堂检测
1.一个两位数,十位数字与个位数字的和为6,且这个两位数不大于42,则这样的两位数有
个.
4
当堂检测
1.一个两位数,十位数字与个位数字的和为6,且这个两位数不大于42,则这样的两位数有
个.
2.能使不等式
成立的x的最大整数
是
.
4
-1
当堂检测
1.一个两位数,十位数字与个位数字的和为6,且这个两位数不大于42,则这样的两位数有
个.
2.能使不等式
成立的x的最大整数
是
.
3.不等式
的解集是
则m的值为_________
4
-1
4
课堂小结
解一元一次不等式的步骤:
1.去分母
2.去括号
3.
移项
4.
合并同类项
5.
系数化为
1
注意:利用不等式的性质3,不等式两边同乘或除以负数时,不等号方向改变.
一元一次不等式定义:
只含有一个未知数,且未知数的次数是1的不等式
1.订正9.2.1一元一次不等式(1)导学案;
2.完成9.2.1一元一次不等式(1)自助餐;
3.预习课本P124-125;
4.完成9.2.1一元一次不等式(2)导学案.
布置作业
