华东师大版数学七年级下9.1.2 三角形内角和与外角和课件(22张PPT)
文档属性
| 名称 | 华东师大版数学七年级下9.1.2 三角形内角和与外角和课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 963.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-04 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
三角形的内角和与外角和
——葫芦岛市第六初级中学
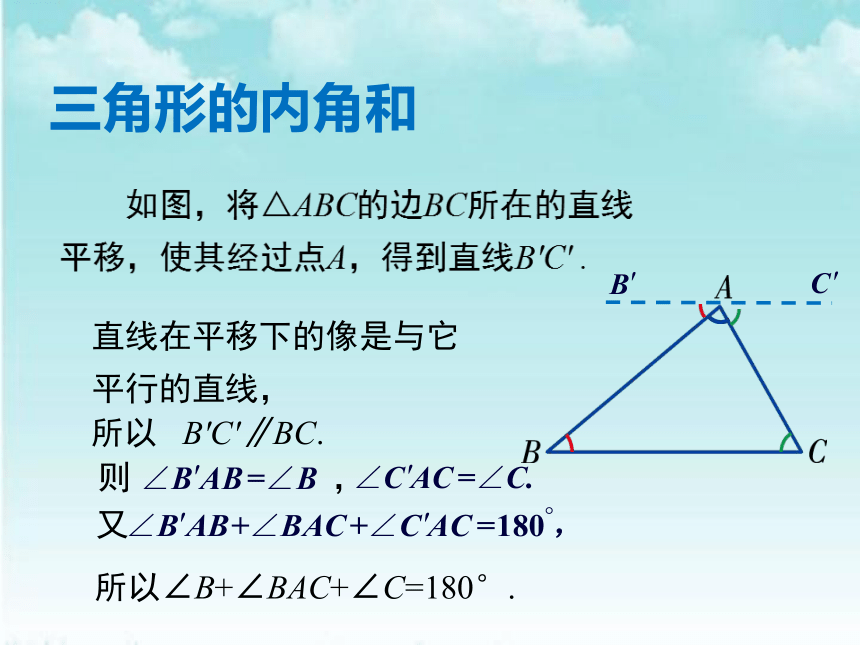
直线在平移下的像是与它
平行的直线,
所以
B'C'∥BC.
所以∠B+∠BAC+∠C=180°.
三角形的内角和
三角形的内角和等于180°.
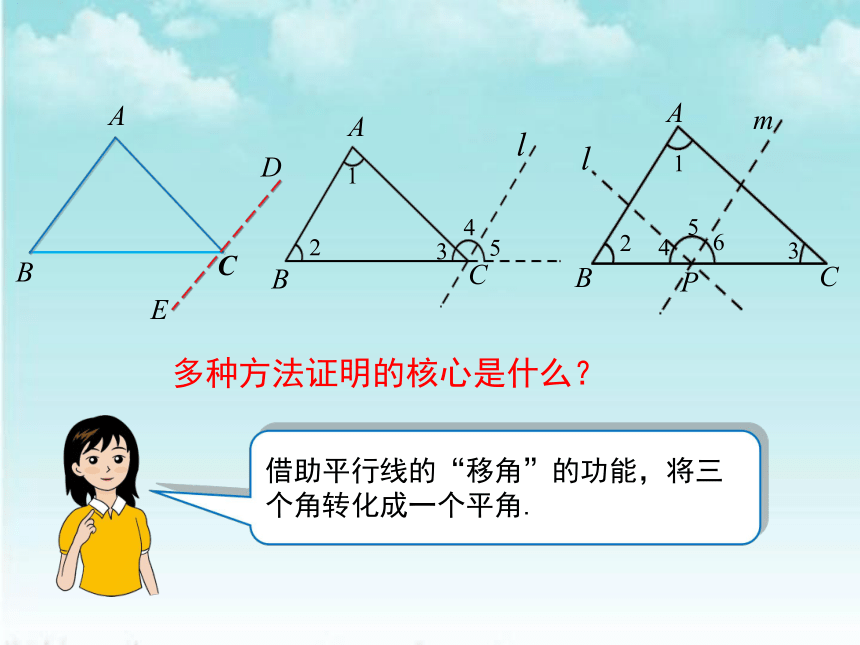
多种方法证明的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
如图,在△ABC中,
∠BAC=40
°,
∠B=75
°,
AD是△ABC的角平分线,求∠ADB的度数.
解:
由∠BAC=40
°,AD是△ABC的角平分线,得
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
例1
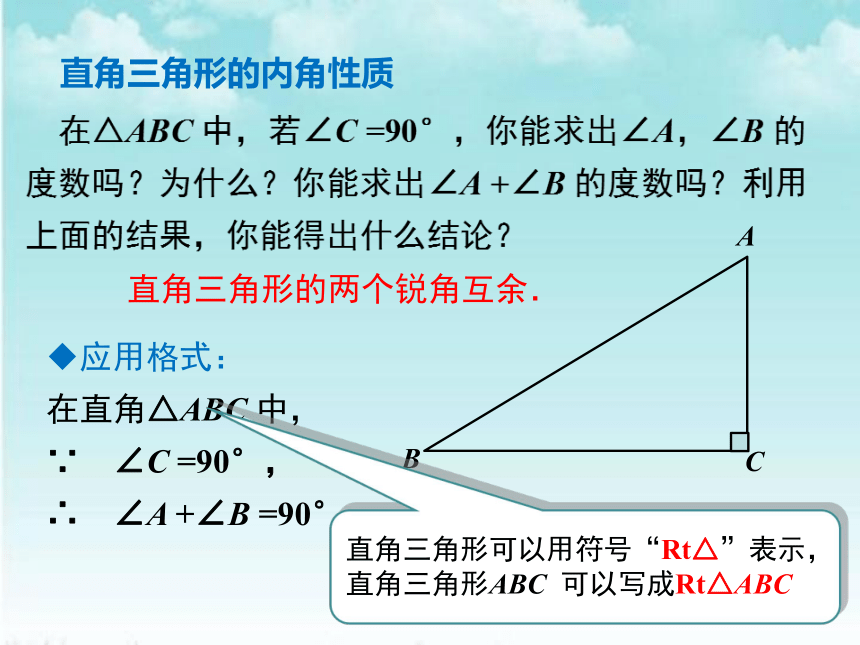
直角三角形的两个锐角互余.
应用格式:
在直角△ABC
中,
∵ ∠C
=90°,
∴ ∠A
+∠B
=90°.
直角三角形可以用符号“Rt△”表示,直角三角形ABC
可以写成Rt△ABC
直角三角形的内角性质
如图,
∠C=∠D=90
°,AD,BC相交于点E.
∠CAE与∠DBE有什么关系?为什么?
解:在Rt△ACE中,
∠CAE=90
°-∠AEC.
在Rt△BDE中,
∠DBE=90
°-∠BED.
∵
∠AEC=
∠BED,
∴
∠CAE=
∠DBE.
例2
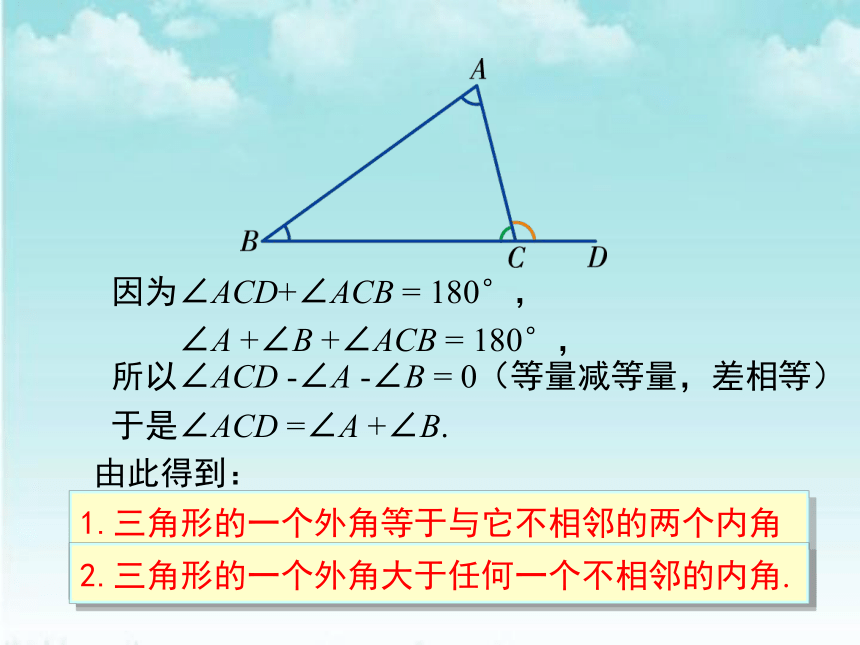
在图中,外角∠ACD与它不相邻的内角∠A,∠B之间有什么大小关系?
我觉得可以利用“三角形的内角和等于180°”的结论.
三角形的外角的性质
因为∠ACD+∠ACB
=
180°,
∠A
+∠B
+∠ACB
=
180°,
所以∠ACD
-∠A
-∠B
=
0(等量减等量,差相等)
于是∠ACD
=∠A
+∠B.
1.三角形的一个外角等于与它不相邻的两个内角的和.
由此得到:
2.三角形的一个外角大于任何一个不相邻的内角.
如图,∠CAD=100°,∠B=30°,求∠C
的度数.
解:因为∠B+∠C=∠CAD,
所以∠C=∠CAD-∠B,
所以∠C=100°-30°=70°.
练一练
如图,
∠BAE,
∠CBF,
∠ACD是△ABC的三个外角,它们的和是多少?
解:由三角形的一个外角等于与它不相邻的两个内角的和,得
∠BAE=
∠2+
∠3,
∠CBF=
∠1+
∠3,
∠ACD=
∠1+
∠2.
又知∠1+
∠2+
∠3=180
°,
所以∠BAE+
∠CBF+
∠ACD
=2(∠1+
∠2+
∠3)=360
°.
你还有其他解法吗?
方法二:如图,∠BAE+∠1=180
°
①
,
∠CBF
+∠2=180
°
②,
∠ACD
+∠3=180
°
③,
又知∠1+
∠2+
∠3=180
°,
①+
②+
③得
∠BAE+
∠CBF+
∠ACD
+(∠1+
∠2+
∠3)=540
°,
所以∠BAE+
∠CBF+
∠ACD=540
°-180°=360°.
三角形的外角和等于360°.
∠BAE+
∠CBF+
∠ACD=2(∠1+
∠2+
∠3)=360
°.
(一题多解)如图,计算∠BDC.
思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.
例3
解:(解法一)连接AD并延长于点E.
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
因为∠BDC=∠3+∠4,∠BAC=∠1+∠2,
所以∠BDC=∠BAC+∠ABD+∠ACD
=51°
+20°+30°=101°.
E
)
)
1
2
)
3
)
4
E
)
1
(解法二)延长BD交AC于点E.
在△ABE中,∠1=∠ABE+∠BAE,
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC=∠BAC+∠ABD+∠ACD
=51°
+20°+30°
=101°.
(解法三)连接延长CD交AB于点F.(解题过程同解法二)
)
2
2
(
重要发现:
∠BDC=
∠1+
∠2+
∠3.
如图,D是△ABC的BC边上的一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.求:
(1)∠B的度数.
(2)∠C的度数.
解:(1)∵∠ADC是△ABD的一个外角,
∴∠ADC=∠B+∠BAD,
又∵∠ADC=80°,∠B=∠BAD,
∴∠B=∠ADC=
×80°=
40°;
(2)在△ABC中,
∵∠BAC+∠B+∠C=180°,
∴∠C=180°-∠B-∠BAC=180°-40°-70°=70°.
例4
1.已知△ABC中,∠A=
70°,∠C=30°,∠B=
______.
2.直角三角形一个锐角为70°,另一个锐角是_______.
3.在△ABC中,∠A=80°,∠B=∠C,则∠C=_______.
80°
20°
50°
4.如图,AD是△ABC的角平分线,∠B=
36°,
∠C=
76°,则∠DAC的度数为________.
34°
5
.如图,D是△ABC的BC边上一点,∠B=∠BAD,
∠ADC=80°,∠BAC=70°,求:(1)∠B
的度数;
(2)∠C的度数.
在△ABC中:
∠B+∠BAC+∠C=180°,
∠C=180?-40?-70?=70°.
解:因为∠ADC是△ABD的外角.
所以∠ADC=∠B+∠BAD=80°.
又因为∠B=∠BAD,
40°
A
B
C
D
三角形的内角
三角形的
内角和定理
证明
了解添加辅助线的方法及其目的
内容
三角形内角和等于180
°
直角三角形的两锐角互余
小结
三角形的外角
定义
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线
性质
三角形的一个外角等于与它不相邻的两个内角的和
三角形的外角和
三角形的外角和等于360
°
三角形的内角和与外角和
——葫芦岛市第六初级中学
直线在平移下的像是与它
平行的直线,
所以
B'C'∥BC.
所以∠B+∠BAC+∠C=180°.
三角形的内角和
三角形的内角和等于180°.
多种方法证明的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
如图,在△ABC中,
∠BAC=40
°,
∠B=75
°,
AD是△ABC的角平分线,求∠ADB的度数.
解:
由∠BAC=40
°,AD是△ABC的角平分线,得
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
例1
直角三角形的两个锐角互余.
应用格式:
在直角△ABC
中,
∵ ∠C
=90°,
∴ ∠A
+∠B
=90°.
直角三角形可以用符号“Rt△”表示,直角三角形ABC
可以写成Rt△ABC
直角三角形的内角性质
如图,
∠C=∠D=90
°,AD,BC相交于点E.
∠CAE与∠DBE有什么关系?为什么?
解:在Rt△ACE中,
∠CAE=90
°-∠AEC.
在Rt△BDE中,
∠DBE=90
°-∠BED.
∵
∠AEC=
∠BED,
∴
∠CAE=
∠DBE.
例2
在图中,外角∠ACD与它不相邻的内角∠A,∠B之间有什么大小关系?
我觉得可以利用“三角形的内角和等于180°”的结论.
三角形的外角的性质
因为∠ACD+∠ACB
=
180°,
∠A
+∠B
+∠ACB
=
180°,
所以∠ACD
-∠A
-∠B
=
0(等量减等量,差相等)
于是∠ACD
=∠A
+∠B.
1.三角形的一个外角等于与它不相邻的两个内角的和.
由此得到:
2.三角形的一个外角大于任何一个不相邻的内角.
如图,∠CAD=100°,∠B=30°,求∠C
的度数.
解:因为∠B+∠C=∠CAD,
所以∠C=∠CAD-∠B,
所以∠C=100°-30°=70°.
练一练
如图,
∠BAE,
∠CBF,
∠ACD是△ABC的三个外角,它们的和是多少?
解:由三角形的一个外角等于与它不相邻的两个内角的和,得
∠BAE=
∠2+
∠3,
∠CBF=
∠1+
∠3,
∠ACD=
∠1+
∠2.
又知∠1+
∠2+
∠3=180
°,
所以∠BAE+
∠CBF+
∠ACD
=2(∠1+
∠2+
∠3)=360
°.
你还有其他解法吗?
方法二:如图,∠BAE+∠1=180
°
①
,
∠CBF
+∠2=180
°
②,
∠ACD
+∠3=180
°
③,
又知∠1+
∠2+
∠3=180
°,
①+
②+
③得
∠BAE+
∠CBF+
∠ACD
+(∠1+
∠2+
∠3)=540
°,
所以∠BAE+
∠CBF+
∠ACD=540
°-180°=360°.
三角形的外角和等于360°.
∠BAE+
∠CBF+
∠ACD=2(∠1+
∠2+
∠3)=360
°.
(一题多解)如图,计算∠BDC.
思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.
例3
解:(解法一)连接AD并延长于点E.
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
因为∠BDC=∠3+∠4,∠BAC=∠1+∠2,
所以∠BDC=∠BAC+∠ABD+∠ACD
=51°
+20°+30°=101°.
E
)
)
1
2
)
3
)
4
E
)
1
(解法二)延长BD交AC于点E.
在△ABE中,∠1=∠ABE+∠BAE,
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC=∠BAC+∠ABD+∠ACD
=51°
+20°+30°
=101°.
(解法三)连接延长CD交AB于点F.(解题过程同解法二)
)
2
2
(
重要发现:
∠BDC=
∠1+
∠2+
∠3.
如图,D是△ABC的BC边上的一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.求:
(1)∠B的度数.
(2)∠C的度数.
解:(1)∵∠ADC是△ABD的一个外角,
∴∠ADC=∠B+∠BAD,
又∵∠ADC=80°,∠B=∠BAD,
∴∠B=∠ADC=
×80°=
40°;
(2)在△ABC中,
∵∠BAC+∠B+∠C=180°,
∴∠C=180°-∠B-∠BAC=180°-40°-70°=70°.
例4
1.已知△ABC中,∠A=
70°,∠C=30°,∠B=
______.
2.直角三角形一个锐角为70°,另一个锐角是_______.
3.在△ABC中,∠A=80°,∠B=∠C,则∠C=_______.
80°
20°
50°
4.如图,AD是△ABC的角平分线,∠B=
36°,
∠C=
76°,则∠DAC的度数为________.
34°
5
.如图,D是△ABC的BC边上一点,∠B=∠BAD,
∠ADC=80°,∠BAC=70°,求:(1)∠B
的度数;
(2)∠C的度数.
在△ABC中:
∠B+∠BAC+∠C=180°,
∠C=180?-40?-70?=70°.
解:因为∠ADC是△ABD的外角.
所以∠ADC=∠B+∠BAD=80°.
又因为∠B=∠BAD,
40°
A
B
C
D
三角形的内角
三角形的
内角和定理
证明
了解添加辅助线的方法及其目的
内容
三角形内角和等于180
°
直角三角形的两锐角互余
小结
三角形的外角
定义
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线
性质
三角形的一个外角等于与它不相邻的两个内角的和
三角形的外角和
三角形的外角和等于360
°
