直线与平面垂直的判定
图片预览





文档简介
(共24张PPT)
问题引入
讲授新课
课堂练习
小结
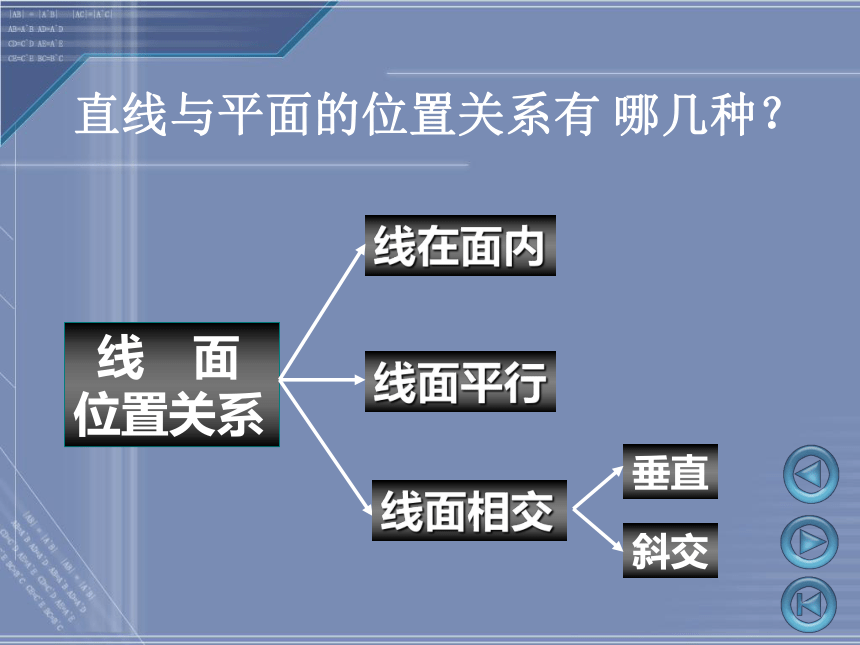
直线与平面的位置关系有 哪几种?
线 面
位置关系
线在面内
线面平行
垂直
斜交
线面相交
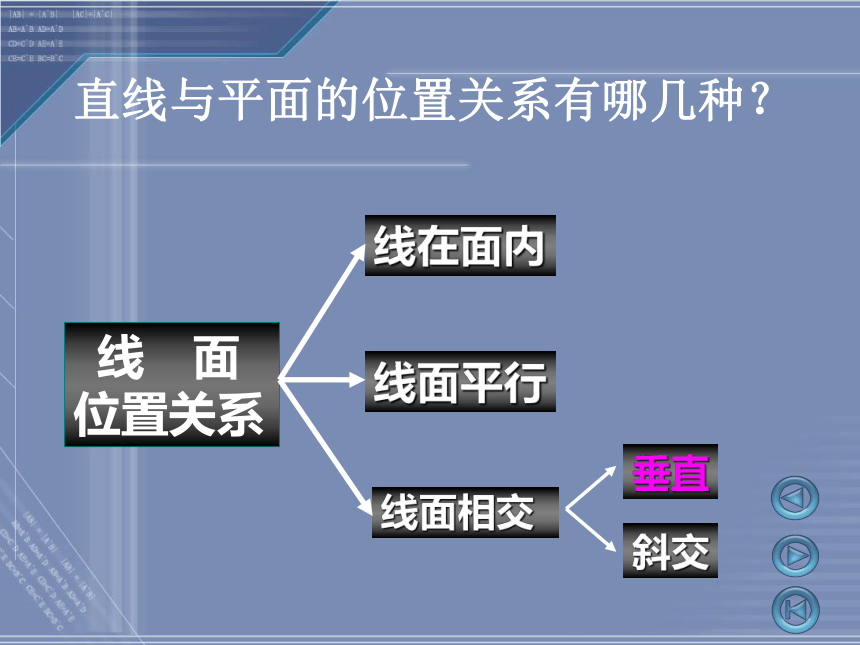
直线与平面的位置关系有哪几种?
线 面
位置关系
线在面内
线面平行
垂直
斜交
线面相交
如果一条直线与一个平面内
任何一条直线都垂直,我们就说
这条直线与这个平面相互垂直。
1、 线面垂直的定义:
判断下列命题是否正确?
若一条直线与一个平面内的无数条直线垂直,则这条直线与这个平面 垂直。
( × )
如果一条直线垂直于平面内的两条相交直线,那么这条直线就垂直于这个平面。
2、线面垂直的判定定理:
如果一条直线垂直于平面内的两条相交直线,那么这条直线就垂直于这个平面。
2、线面垂直的判定定理:
m
n
m
n
m
n
m
n
g
g
g
g
l
l
l
l
⑴
⑵
⑶
⑷
B
B
B
B
使AB=A’B
B
A’
A
m
n
g
C
D
E
l
B
A’
A
m
n
g
C
D
E
l
所以AC=A’C
因为l⊥m且
AB=A’B
B
A’
A
m
n
g
C
D
E
l
同理AD=A’D
B
A’
A
m
n
g
C
D
E
l
AE=A’E
B
A’
A
m
n
g
C
D
E
l
△ACE≌△A’CE
B
A’
A
m
n
g
C
D
E
l
△ACD≌△A’CD
证明:如图,设g是平面α内的任一条直线,则:
在直线l上点B的两侧分别取点A、A’,使
|AB| = |A’B|,在平面α内任作一条直线CD,与
直线m、n 、g分别交于点C、D、E,连接AC、
A’C、AD、A’D、AE、A’E,则有:
AC=A’C ,AD=A’D ,CD=CD
∴△ACD≌ △A’CD (SSS)
得∠ACE= ∠A’CE
∴△ACE≌ △A’CE (SAS)
得AE=A’E
∴ g是AA’的垂直平分线,即l⊥g 。
∴ l⊥α
A
A’
C
D
E
B
m
n
g
已知:m 、n是α内的两条相交直线 ,l∩α=B ,且l⊥m,
l⊥n。
求证:l⊥α 。
l
α
(2)如果一条直线和一个平面内的两条直线垂直,此直线是否和平面垂直?
问题
(1)如果一条直线和一个平面内的一条直线垂直,此直线是否和平面垂直?
例1 已知: ∩ =CD ,EA⊥ 于A,
EB⊥ 于B,如图所示。
求证:CD⊥AB。
E
A
B
C
D
(1)、 过一点和一个平面垂直的直线只有一条。( )
(2)、过一点和一条直线垂直的平面只有一个。( )
判断下列命题是否正确?
想一想
√
√
1、 线面垂直的定义:如果一条直线与一个平面内任何一条直线都垂直,我们就说这条直线与这个平面相互垂直。
2、 线面垂直的判定定理: 如果一条直线垂直于平面内的两条相交直线,那么这条直线就垂直于这个平面。
1、 线面垂直的定义:如果一条直线与一个平面内任何一条直线都垂直,我们就说这条直线与这个平面相互垂直。
2、 线面垂直的判定定理: 如果一条直线垂直于平面内的两条相交直线,那么这条直线就垂直于这个平面。
线线垂直
线面垂直
判定定理
定 义
问题引入
讲授新课
课堂练习
小结
直线与平面的位置关系有 哪几种?
线 面
位置关系
线在面内
线面平行
垂直
斜交
线面相交
直线与平面的位置关系有哪几种?
线 面
位置关系
线在面内
线面平行
垂直
斜交
线面相交
如果一条直线与一个平面内
任何一条直线都垂直,我们就说
这条直线与这个平面相互垂直。
1、 线面垂直的定义:
判断下列命题是否正确?
若一条直线与一个平面内的无数条直线垂直,则这条直线与这个平面 垂直。
( × )
如果一条直线垂直于平面内的两条相交直线,那么这条直线就垂直于这个平面。
2、线面垂直的判定定理:
如果一条直线垂直于平面内的两条相交直线,那么这条直线就垂直于这个平面。
2、线面垂直的判定定理:
m
n
m
n
m
n
m
n
g
g
g
g
l
l
l
l
⑴
⑵
⑶
⑷
B
B
B
B
使AB=A’B
B
A’
A
m
n
g
C
D
E
l
B
A’
A
m
n
g
C
D
E
l
所以AC=A’C
因为l⊥m且
AB=A’B
B
A’
A
m
n
g
C
D
E
l
同理AD=A’D
B
A’
A
m
n
g
C
D
E
l
AE=A’E
B
A’
A
m
n
g
C
D
E
l
△ACE≌△A’CE
B
A’
A
m
n
g
C
D
E
l
△ACD≌△A’CD
证明:如图,设g是平面α内的任一条直线,则:
在直线l上点B的两侧分别取点A、A’,使
|AB| = |A’B|,在平面α内任作一条直线CD,与
直线m、n 、g分别交于点C、D、E,连接AC、
A’C、AD、A’D、AE、A’E,则有:
AC=A’C ,AD=A’D ,CD=CD
∴△ACD≌ △A’CD (SSS)
得∠ACE= ∠A’CE
∴△ACE≌ △A’CE (SAS)
得AE=A’E
∴ g是AA’的垂直平分线,即l⊥g 。
∴ l⊥α
A
A’
C
D
E
B
m
n
g
已知:m 、n是α内的两条相交直线 ,l∩α=B ,且l⊥m,
l⊥n。
求证:l⊥α 。
l
α
(2)如果一条直线和一个平面内的两条直线垂直,此直线是否和平面垂直?
问题
(1)如果一条直线和一个平面内的一条直线垂直,此直线是否和平面垂直?
例1 已知: ∩ =CD ,EA⊥ 于A,
EB⊥ 于B,如图所示。
求证:CD⊥AB。
E
A
B
C
D
(1)、 过一点和一个平面垂直的直线只有一条。( )
(2)、过一点和一条直线垂直的平面只有一个。( )
判断下列命题是否正确?
想一想
√
√
1、 线面垂直的定义:如果一条直线与一个平面内任何一条直线都垂直,我们就说这条直线与这个平面相互垂直。
2、 线面垂直的判定定理: 如果一条直线垂直于平面内的两条相交直线,那么这条直线就垂直于这个平面。
1、 线面垂直的定义:如果一条直线与一个平面内任何一条直线都垂直,我们就说这条直线与这个平面相互垂直。
2、 线面垂直的判定定理: 如果一条直线垂直于平面内的两条相交直线,那么这条直线就垂直于这个平面。
线线垂直
线面垂直
判定定理
定 义
