同底数幂的乘法

(共26张PPT)
考考你：
光的速度约为3×105千米/秒，太阳光
照射到地球大约需要5×102秒. 地球距离
太阳大约有多远？
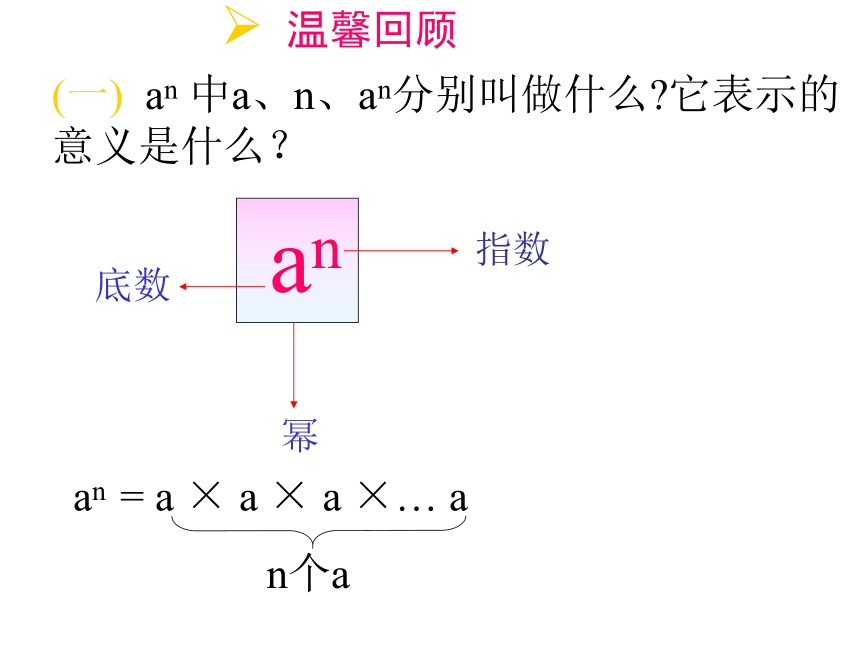
(一) an 中a、n、an分别叫做什么 它表示的 意义是什么？
an
底数
幂
指数
温馨回顾
an = a × a × a ×… a
n个a
25表示什么？
10×10×10×10×10 可以写成什么形式
（二）：
25 = .

2×2×2×2×2
105
10×10×10×10×10 = .
(乘方的意义）
(乘方的意义）
式子103×102的意义是什么？
尝试探究：
这个式子中的两个因式有何特点？
请同学们先根据自己的理解，解答下列各题.
103 ×102 = = 10（ ）
23 ×22 = =2（ ）
5
（2×2×2）×（2×2）
5
a3×a2 = = a（ ） .
5
（a a a）
（a a）
=2×2×2×2×2
= a a a a a
3个a
2个a
5个a
（10×10×10）×（10×10）
交流与发现：
请同学们观察由上面各题得出的等式左右两边，底数、指数有什么关系？
103 ×102 = 10（ ）
23 ×22 = 2（ ）
a3× a2 = a（ ）
5
5
5
猜想: am · an= (当m、n都是正整数)
　　分组讨论，并尝试证明你的猜想是否正确.
3+2
3+2
3+2
= 10（ ）；
= 2（ ）；
= a（ ） 。
猜想: am · an= (当m、n都是正整数)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即
am · an = am+n (当m、n都是正整数)
（aa…a）
（aa…a）
（乘方的意义）
（乘法结合律）
（乘方的意义）
真不错，你的猜想是正确的！
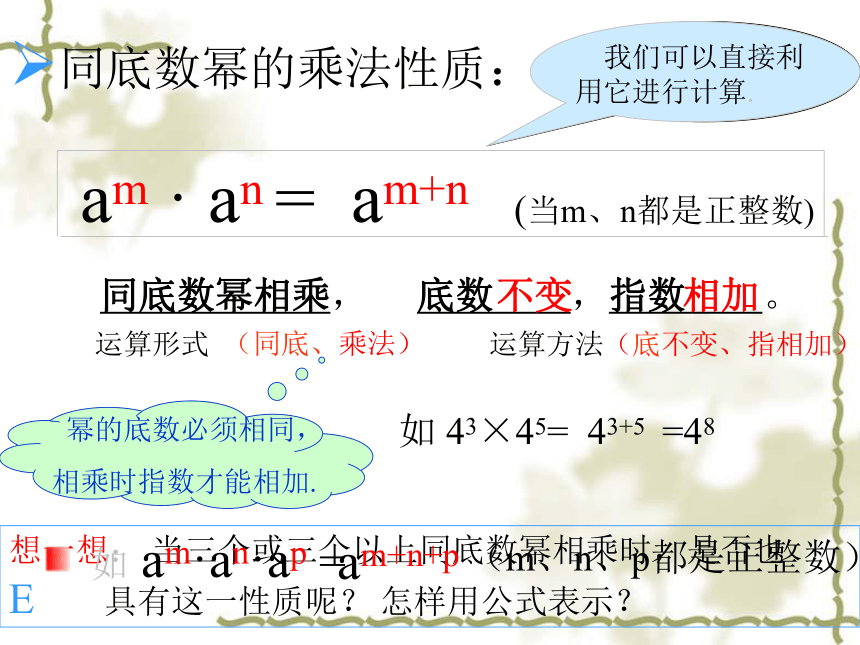
am · an = am+n (当m、n都是正整数)
同底数幂相乘，
想一想： 当三个或三个以上同底数幂相乘时，是否也 　 具有这一性质呢？ 怎样用公式表示？
底数　　，指数　　。
不变
相加
同底数幂的乘法性质：
　请你尝试用文字概括这个结论。
我们可以直接利用它进行计算.
如 43×45=
43+5
=48
如 am·an·ap =
am+n+p
（m、n、p都是正整数）
运算形式
运算方法
（同底、乘法）
（底不变、指相加）
幂的底数必须相同，
相乘时指数才能相加.
例1计算下列各式,结果用幂的形式表示
(1) 7 8 × 7 3 (2) (-2) 8 × (-2)7
解: (1) 7 8 × 7 3 = 7 8+3 = 7 11
(2) (-2) 8 × (-2)7 = (-2) 8 +7 = (-2)15 = -215
(3) x3 · x5 = x3+5 = x8
(4) (a-b)2 (a-b) = (a-b)2+1 = (a-b)3
(3) x3 · x5 (4) (a-b)2 (a-b)
学以致用
例2.计算：
（1）23×24×25 （2）y · y2 · y3
解：（1）23×24×25=23+4+5=212
（2）y · y2 · y3 = y1+2+3=y6
考考你：光的速度约为3×105千米/秒，太阳光照射到地球大约需要5×102秒.地球距离太阳大约有多远？
解：3×105×5×102
=15×107
=1.5×108(千米)
地球距离太阳大约有1.5×108千米.
飞行这么远的距离，一架喷气式客机大约要20年呢！
练习一
1. 计算：（抢答）
(1011 )
( a10 )
（ x10 ）
（ b6 ）
（2） a7 ·a3
（3） x5 ·x5
（4） b5 · b
（1） 105×106
Good!
看谁反应快
2. 计算：（必答）
（1）x10 · x （2）10×102×104
（3） x5 ·x ·x3 （4）y4·y3·y2·y
解：
（1）x10 ·x = x10+1= x11
（2）10×102×104 =101+2+4 =107
（3）x5 ·x ·x3 = x5+1+3 = x9
（4）y4 ·y3 ·y2 ·y= y4+3+2+1= y10
练习二
下面的计算对不对？如果不对，怎样改正？
（1）b5 · b5= 2b5 （ ） （2）b5 + b5 = b10 （ ）
（3）x5 ·x5 = x25 ( ) （4）y5 · y5 = 2y10 ( )
（5）c · c3 = c3 ( ) （6）m + m3 = m4 ( )
m + m3 = m + m3
b5 · b5= b10
b5 + b5 = 2b5
x5 · x5 = x10
y5 · y5 =y10
c · c3 = c4
×
×
×
×
×
×
了不起！
测测你的判断力
填空：
（1）x5 ·（ ）=　x 8 （2）a ·（ ）=　a6
（3）x · x3（ ）= x7 （4）xm ·（　 ）＝ｘ3m
变式训练
x3
a5
x3
ｘ2m
真棒！
真不错！
你真行！
太棒了！
同底数幂相乘，　
底数　　 指数　
am · an = am+n (m、n正整数)
小结
我学到了什么？
知识　
　　方法　
　“特殊→一般→特殊”
　 例子 公式 应用
不变，
相加.
第一关
第二关
第三关
第四关
知识拓展
填空：
（1）x5 .（ ）=　x 2011
（2）x4· x3= 27 求Ｘ的值
X2006
X= 2
2. 计算：
a2 a3 + a a4
=2a5
3.如果an-2 an+1=a11,
则n= .
6
4．已知：am=2，an=3.
　求am+n .
课本p119习题14.1 A组第1题